Diff-PIC: Revolutionizing Particle-In-Cell Simulation for Advancing Nuclear Fusion with Diffusion Models

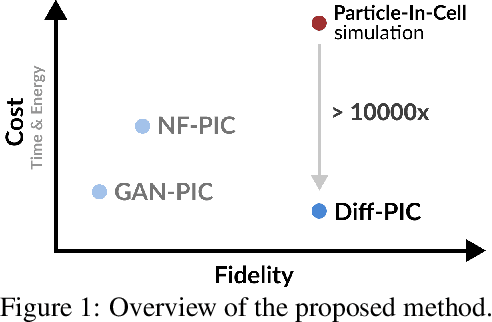
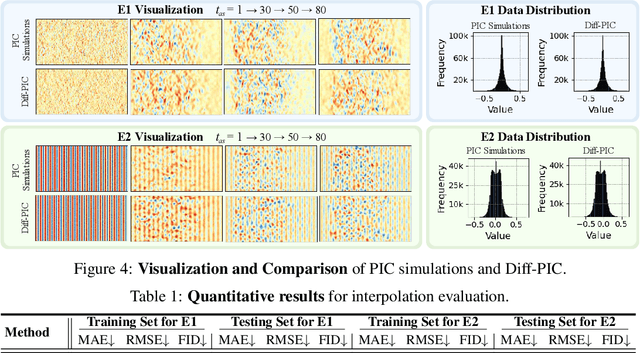
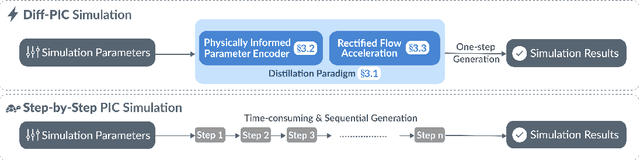
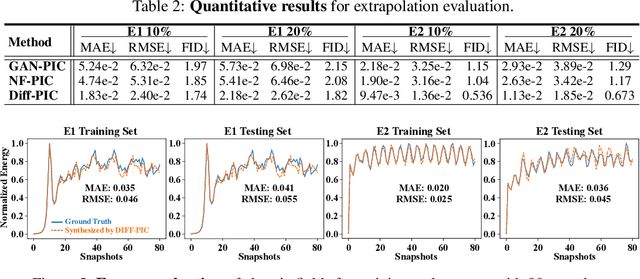
Sustainable energy is a crucial global challenge, and recent breakthroughs in nuclear fusion ignition underscore the potential of harnessing energy extracted from nuclear fusion in everyday life, thereby drawing significant attention to fusion ignition research, especially Laser-Plasma Interaction (LPI). Unfortunately, the complexity of LPI at ignition scale renders theory-based analysis nearly impossible -- instead, it has to rely heavily on Particle-in-Cell (PIC) simulations, which is extremely computationally intensive, making it a major bottleneck in advancing fusion ignition. In response, this work introduces Diff-PIC, a novel paradigm that leverages conditional diffusion models as a computationally efficient alternative to PIC simulations for generating high-fidelity scientific data. Specifically, we design a distillation paradigm to distill the physical patterns captured by PIC simulations into diffusion models, demonstrating both theoretical and practical feasibility. Moreover, to ensure practical effectiveness, we provide solutions for two critical challenges: (1) We develop a physically-informed conditional diffusion model that can learn and generate meaningful embeddings for mathematically continuous physical conditions. This model offers algorithmic generalization and adaptable transferability, effectively capturing the complex relationships between physical conditions and simulation outcomes; and (2) We employ the rectified flow technique to make our model a one-step conditional diffusion model, enhancing its efficiency further while maintaining high fidelity and physical validity. Diff-PIC establishes a new paradigm for using diffusion models to overcome the computational barriers in nuclear fusion research, setting a benchmark for future innovations and advancements in this field.

Inertial Confinement Fusion Forecasting via LLMs

Controlled fusion energy is deemed pivotal for the advancement of human civilization. In this study, we introduce $\textbf{Fusion-LLM}$, a novel integration of Large Language Models (LLMs) with classical reservoir computing paradigms tailored to address challenges in Inertial Confinement Fusion ($\texttt{ICF}$). Our approach offers several key contributions: Firstly, we propose the $\textit{LLM-anchored Reservoir}$, augmented with a fusion-specific prompt, enabling accurate forecasting of hot electron dynamics during implosion. Secondly, we develop $\textit{Signal-Digesting Channels}$ to temporally and spatially describe the laser intensity across time, capturing the unique characteristics of $\texttt{ICF}$ inputs. Lastly, we design the $\textit{Confidence Scanner}$ to quantify the confidence level in forecasting, providing valuable insights for domain experts to design the $\texttt{ICF}$ process. Extensive experiments demonstrate the superior performance of our method, achieving 1.90 CAE, 0.14 $\texttt{top-1}$ MAE, and 0.11 $\texttt{top-5}$ MAE in predicting Hard X-ray ($\texttt{HXR}$) energies of $\texttt{ICF}$ tasks, which presents state-of-the-art comparisons against concurrent best systems. Additionally, we present $\textbf{Fusion4AI}$, the first $\texttt{ICF}$ benchmark based on physical experiments, aimed at fostering novel ideas in plasma physics research and enhancing the utility of LLMs in scientific exploration. Overall, our work strives to forge an innovative synergy between AI and plasma science for advancing fusion energy.

Learning Best-in-Class Policies for the Predict-then-Optimize Framework

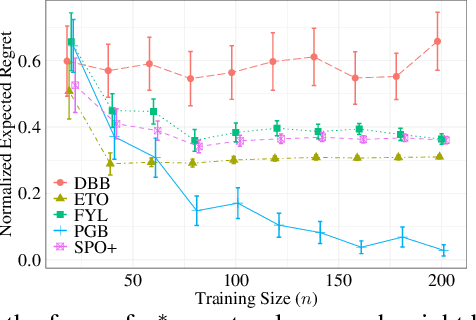
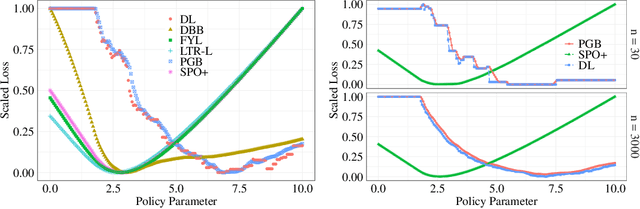
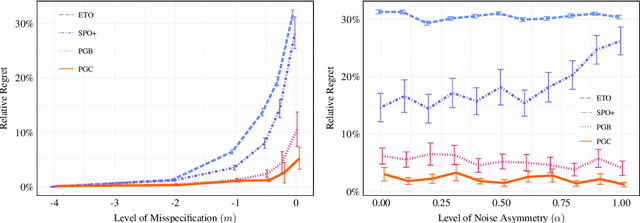
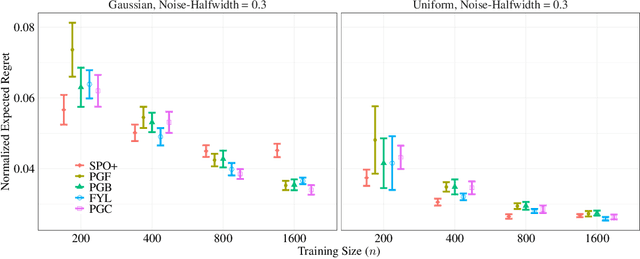
We propose a novel family of decision-aware surrogate losses, called Perturbation Gradient (PG) losses, for the predict-then-optimize framework. These losses directly approximate the downstream decision loss and can be optimized using off-the-shelf gradient-based methods. Importantly, unlike existing surrogate losses, the approximation error of our PG losses vanishes as the number of samples grows. This implies that optimizing our surrogate loss yields a best-in-class policy asymptotically, even in misspecified settings. This is the first such result in misspecified settings and we provide numerical evidence confirming our PG losses substantively outperform existing proposals when the underlying model is misspecified and the noise is not centrally symmetric. Insofar as misspecification is commonplace in practice -- especially when we might prefer a simpler, more interpretable model -- PG losses offer a novel, theoretically justified, method for computationally tractable decision-aware learning.

Augmented Electronic Ising Machine as an Effective SAT Solver

With the slowdown of improvement in conventional von Neumann systems, increasing attention is paid to novel paradigms such as Ising machines. They have very different approach to NP-complete optimization problems. Ising machines have shown great potential in solving binary optimization problems like MaxCut. In this paper, we present an analysis of these systems in satisfiability (SAT) problems. We demonstrate that, in the case of 3-SAT, a basic architecture fails to produce meaningful acceleration, thanks in no small part to the relentless progress made in conventional SAT solvers. Nevertheless, careful analysis attributes part of the failure to the lack of two important components: cubic interactions and efficient randomization heuristics. To overcome these limitations, we add proper architectural support for cubic interaction on a state-of-the-art Ising machine. More importantly, we propose a novel semantic-aware annealing schedule that makes the search-space navigation much more efficient than existing annealing heuristics. With experimental analyses, we show that such an Augmented Ising Machine for SAT (AIMS), outperforms state-of-the-art software-based, GPU-based and conventional hardware SAT solvers by orders of magnitude. We also demonstrate AIMS to be relatively robust against device variation and noise.

Debiasing In-Sample Policy Performance for Small-Data, Large-Scale Optimization

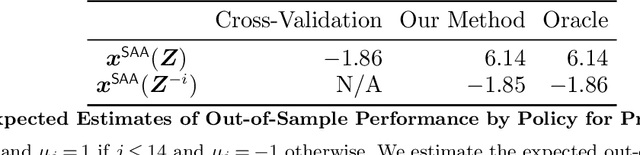
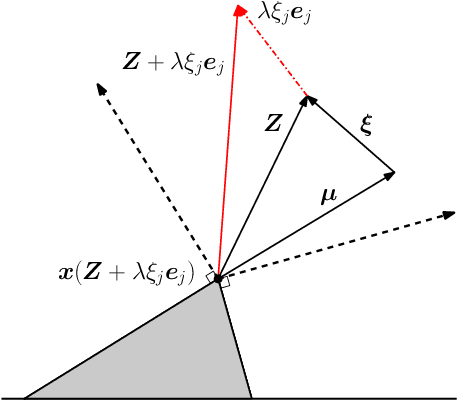
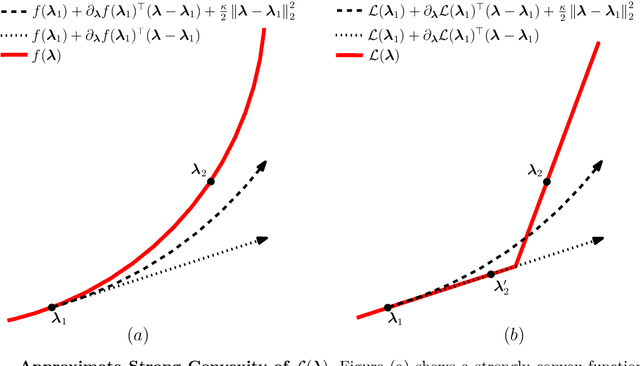
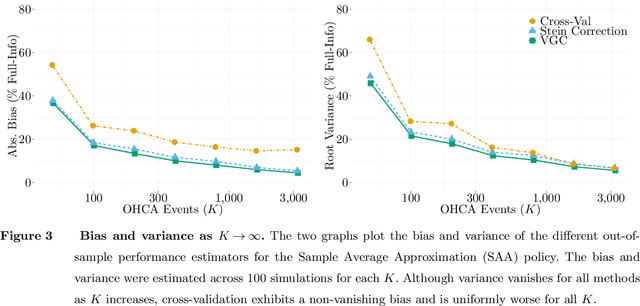
Motivated by the poor performance of cross-validation in settings where data are scarce, we propose a novel estimator of the out-of-sample performance of a policy in data-driven optimization.Our approach exploits the optimization problem's sensitivity analysis to estimate the gradient of the optimal objective value with respect to the amount of noise in the data and uses the estimated gradient to debias the policy's in-sample performance. Unlike cross-validation techniques, our approach avoids sacrificing data for a test set, utilizes all data when training and, hence, is well-suited to settings where data are scarce. We prove bounds on the bias and variance of our estimator for optimization problems with uncertain linear objectives but known, potentially non-convex, feasible regions. For more specialized optimization problems where the feasible region is "weakly-coupled" in a certain sense, we prove stronger results. Specifically, we provide explicit high-probability bounds on the error of our estimator that hold uniformly over a policy class and depends on the problem's dimension and policy class's complexity. Our bounds show that under mild conditions, the error of our estimator vanishes as the dimension of the optimization problem grows, even if the amount of available data remains small and constant. Said differently, we prove our estimator performs well in the small-data, large-scale regime. Finally, we numerically compare our proposed method to state-of-the-art approaches through a case-study on dispatching emergency medical response services using real data. Our method provides more accurate estimates of out-of-sample performance and learns better-performing policies.