Debiasing In-Sample Policy Performance for Small-Data, Large-Scale Optimization

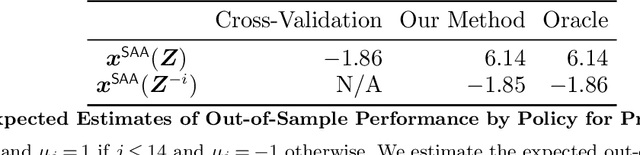
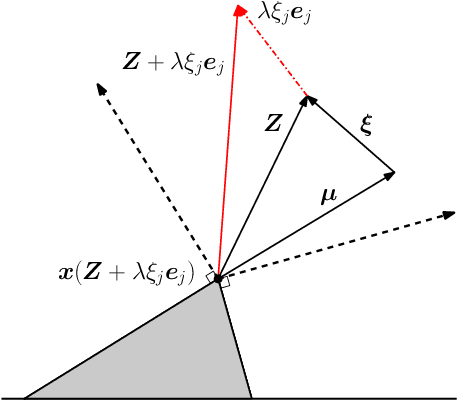
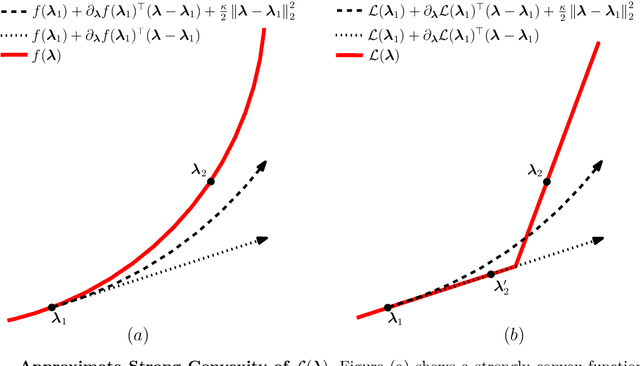
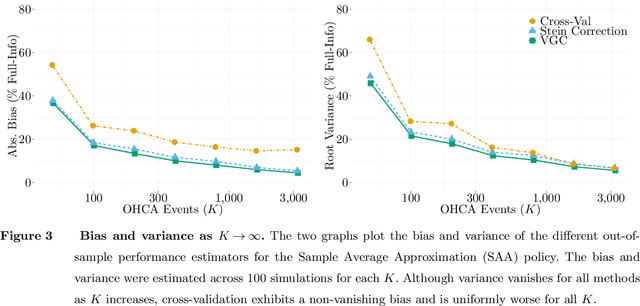
Motivated by the poor performance of cross-validation in settings where data are scarce, we propose a novel estimator of the out-of-sample performance of a policy in data-driven optimization.Our approach exploits the optimization problem's sensitivity analysis to estimate the gradient of the optimal objective value with respect to the amount of noise in the data and uses the estimated gradient to debias the policy's in-sample performance. Unlike cross-validation techniques, our approach avoids sacrificing data for a test set, utilizes all data when training and, hence, is well-suited to settings where data are scarce. We prove bounds on the bias and variance of our estimator for optimization problems with uncertain linear objectives but known, potentially non-convex, feasible regions. For more specialized optimization problems where the feasible region is "weakly-coupled" in a certain sense, we prove stronger results. Specifically, we provide explicit high-probability bounds on the error of our estimator that hold uniformly over a policy class and depends on the problem's dimension and policy class's complexity. Our bounds show that under mild conditions, the error of our estimator vanishes as the dimension of the optimization problem grows, even if the amount of available data remains small and constant. Said differently, we prove our estimator performs well in the small-data, large-scale regime. Finally, we numerically compare our proposed method to state-of-the-art approaches through a case-study on dispatching emergency medical response services using real data. Our method provides more accurate estimates of out-of-sample performance and learns better-performing policies.

A Tractable POMDP for a Class of Sequencing Problems

We consider a partially observable Markov decision problem (POMDP) that models a class of sequencing problems. Although POMDPs are typically intractable, our formulation admits tractable solution. Instead of maintaining a value function over a high-dimensional set of belief states, we reduce the state space to one of smaller dimension, in which grid-based dynamic programming techniques are effective. We develop an error bound for the resulting approximation, and discuss an application of the model to a problem in targeted advertising.

Linearly Parameterized Bandits

We consider bandit problems involving a large (possibly infinite) collection of arms, in which the expected reward of each arm is a linear function of an $r$-dimensional random vector $\mathbf{Z} \in \mathbb{R}^r$, where $r \geq 2$. The objective is to minimize the cumulative regret and Bayes risk. When the set of arms corresponds to the unit sphere, we prove that the regret and Bayes risk is of order $\Theta(r \sqrt{T})$, by establishing a lower bound for an arbitrary policy, and showing that a matching upper bound is obtained through a policy that alternates between exploration and exploitation phases. The phase-based policy is also shown to be effective if the set of arms satisfies a strong convexity condition. For the case of a general set of arms, we describe a near-optimal policy whose regret and Bayes risk admit upper bounds of the form $O(r \sqrt{T} \log^{3/2} T)$.