ASDL: A Unified Interface for Gradient Preconditioning in PyTorch

Gradient preconditioning is a key technique to integrate the second-order information into gradients for improving and extending gradient-based learning algorithms. In deep learning, stochasticity, nonconvexity, and high dimensionality lead to a wide variety of gradient preconditioning methods, with implementation complexity and inconsistent performance and feasibility. We propose the Automatic Second-order Differentiation Library (ASDL), an extension library for PyTorch, which offers various implementations and a plug-and-play unified interface for gradient preconditioning. ASDL enables the study and structured comparison of a range of gradient preconditioning methods.

PipeFisher: Efficient Training of Large Language Models Using Pipelining and Fisher Information Matrices

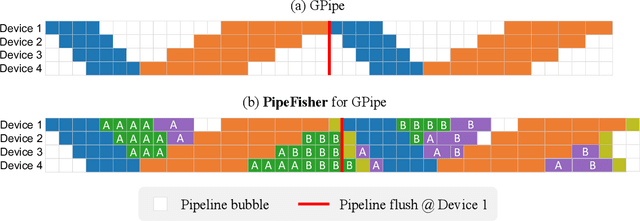
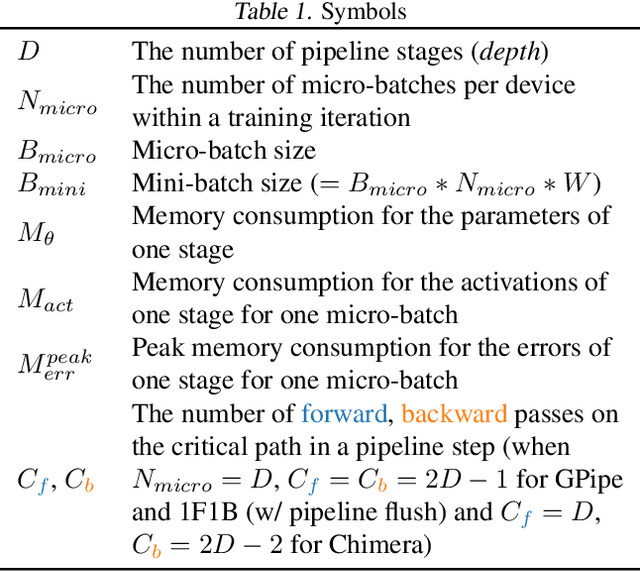
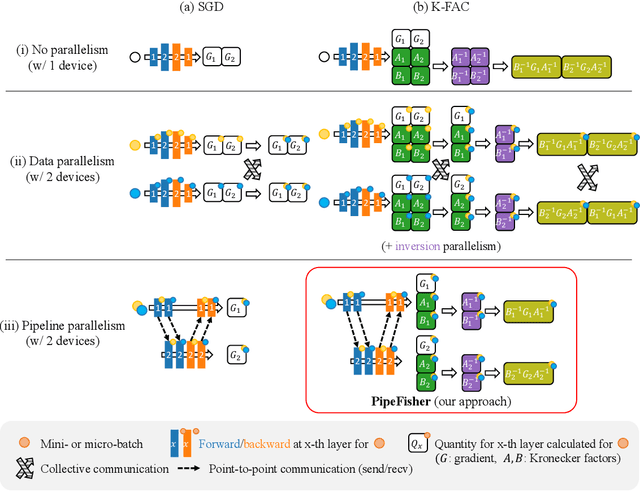
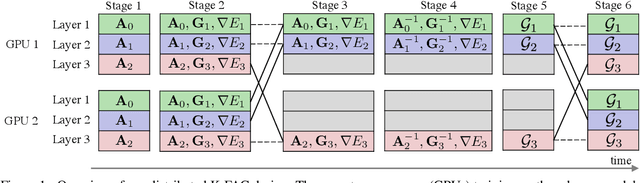
Pipeline parallelism enables efficient training of Large Language Models (LLMs) on large-scale distributed accelerator clusters. Yet, pipeline bubbles during startup and tear-down reduce the utilization of accelerators. Although efficient pipeline schemes with micro-batching and bidirectional pipelines have been proposed to maximize utilization, a significant number of bubbles cannot be filled using synchronous forward and backward passes. To address this problem, we suggest that extra work be assigned to the bubbles to gain auxiliary benefits in LLM training. As an example in this direction, we propose PipeFisher, which assigns the work of K-FAC, a second-order optimization method based on the Fisher information matrix, to the bubbles to accelerate convergence. In Phase 1 pretraining of BERT-Base and -Large models, PipeFisher reduces the (simulated) training time to 50-75% compared to training with a first-order optimizer by greatly improving the accelerator utilization and benefiting from the improved convergence by K-FAC.

Understanding Gradient Regularization in Deep Learning: Efficient Finite-Difference Computation and Implicit Bias

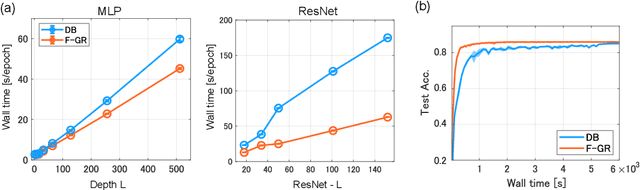
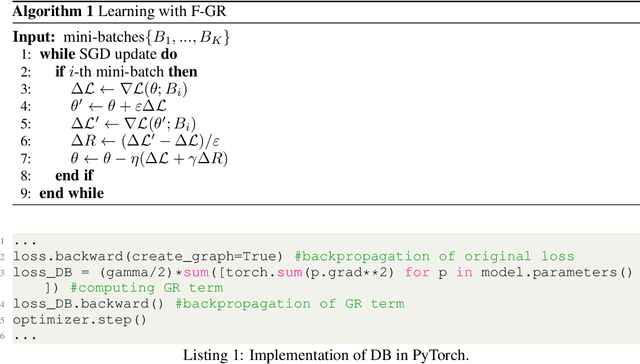
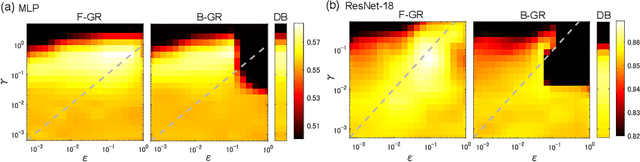
Gradient regularization (GR) is a method that penalizes the gradient norm of the training loss during training. Although some studies have reported that GR improves generalization performance in deep learning, little attention has been paid to it from the algorithmic perspective, that is, the algorithms of GR that efficiently improve performance. In this study, we first reveal that a specific finite-difference computation, composed of both gradient ascent and descent steps, reduces the computational cost for GR. In addition, this computation empirically achieves better generalization performance. Next, we theoretically analyze a solvable model, a diagonal linear network, and clarify that GR has a desirable implicit bias in a certain problem. In particular, learning with the finite-difference GR chooses better minima as the ascent step size becomes larger. Finally, we demonstrate that finite-difference GR is closely related to some other algorithms based on iterative ascent and descent steps for exploring flat minima: sharpness-aware minimization and the flooding method. We reveal that flooding performs finite-difference GR in an implicit way. Thus, this work broadens our understanding of GR in both practice and theory.

Neural Graph Databases

Graph databases (GDBs) enable processing and analysis of unstructured, complex, rich, and usually vast graph datasets. Despite the large significance of GDBs in both academia and industry, little effort has been made into integrating them with the predictive power of graph neural networks (GNNs). In this work, we show how to seamlessly combine nearly any GNN model with the computational capabilities of GDBs. For this, we observe that the majority of these systems are based on, or support, a graph data model called the Labeled Property Graph (LPG), where vertices and edges can have arbitrarily complex sets of labels and properties. We then develop LPG2vec, an encoder that transforms an arbitrary LPG dataset into a representation that can be directly used with a broad class of GNNs, including convolutional, attentional, message-passing, and even higher-order or spectral models. In our evaluation, we show that the rich information represented as LPG labels and properties is properly preserved by LPG2vec, and it increases the accuracy of predictions regardless of the targeted learning task or the used GNN model, by up to 34% compared to graphs with no LPG labels/properties. In general, LPG2vec enables combining predictive power of the most powerful GNNs with the full scope of information encoded in the LPG model, paving the way for neural graph databases, a class of systems where the vast complexity of maintained data will benefit from modern and future graph machine learning methods.

Efficient Quantized Sparse Matrix Operations on Tensor Cores

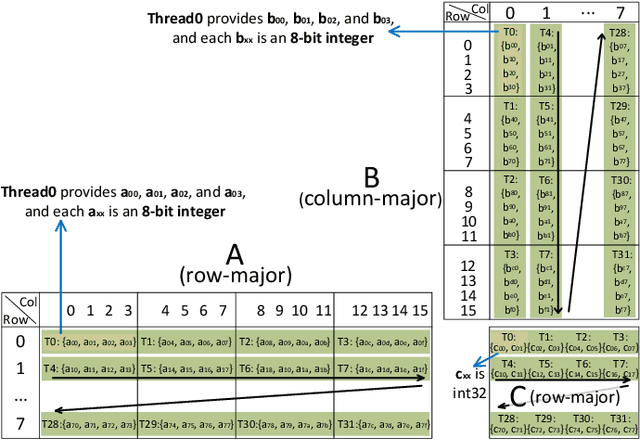
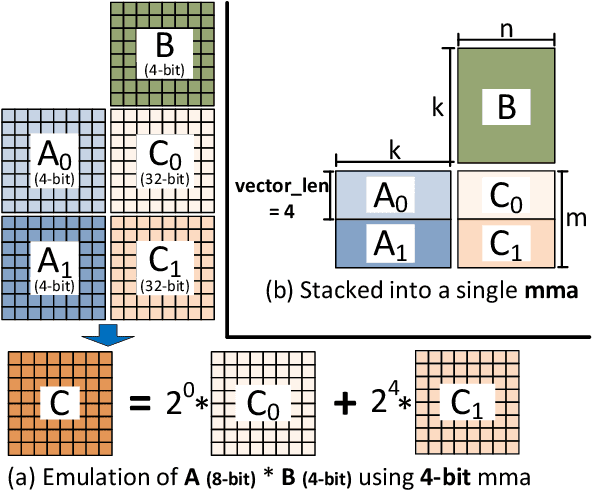
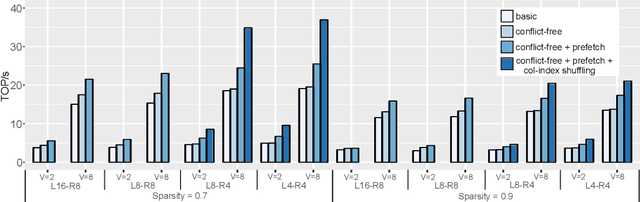
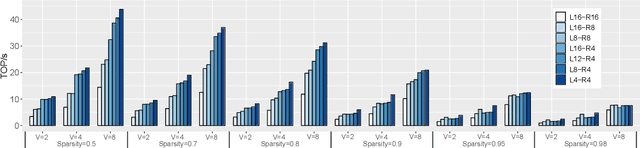
The exponentially growing model size drives the continued success of deep learning, but it brings prohibitive computation and memory cost. From the algorithm perspective, model sparsification and quantization have been studied to alleviate the problem. From the architecture perspective, hardware vendors provide Tensor cores for acceleration. However, it is very challenging to gain practical speedups from sparse, low-precision matrix operations on Tensor cores, because of the strict requirements for data layout and lack of support for efficiently manipulating the low-precision integers. We propose Magicube, a high-performance sparse-matrix library for low-precision integers on Tensor cores. Magicube supports SpMM and SDDMM, two major sparse operations in deep learning with mixed precision. Experimental results on an NVIDIA A100 GPU show that Magicube achieves on average 1.44x (up to 2.37x) speedup over the vendor-optimized library for sparse kernels, and 1.43x speedup over the state-of-the-art with a comparable accuracy for end-to-end sparse Transformer inference.

Understanding Approximate Fisher Information for Fast Convergence of Natural Gradient Descent in Wide Neural Networks

Natural Gradient Descent (NGD) helps to accelerate the convergence of gradient descent dynamics, but it requires approximations in large-scale deep neural networks because of its high computational cost. Empirical studies have confirmed that some NGD methods with approximate Fisher information converge sufficiently fast in practice. Nevertheless, it remains unclear from the theoretical perspective why and under what conditions such heuristic approximations work well. In this work, we reveal that, under specific conditions, NGD with approximate Fisher information achieves the same fast convergence to global minima as exact NGD. We consider deep neural networks in the infinite-width limit, and analyze the asymptotic training dynamics of NGD in function space via the neural tangent kernel. In the function space, the training dynamics with the approximate Fisher information are identical to those with the exact Fisher information, and they converge quickly. The fast convergence holds in layer-wise approximations; for instance, in block diagonal approximation where each block corresponds to a layer as well as in block tri-diagonal and K-FAC approximations. We also find that a unit-wise approximation achieves the same fast convergence under some assumptions. All of these different approximations have an isotropic gradient in the function space, and this plays a fundamental role in achieving the same convergence properties in training. Thus, the current study gives a novel and unified theoretical foundation with which to understand NGD methods in deep learning.

Scalable and Practical Natural Gradient for Large-Scale Deep Learning

Large-scale distributed training of deep neural networks results in models with worse generalization performance as a result of the increase in the effective mini-batch size. Previous approaches attempt to address this problem by varying the learning rate and batch size over epochs and layers, or ad hoc modifications of batch normalization. We propose Scalable and Practical Natural Gradient Descent (SP-NGD), a principled approach for training models that allows them to attain similar generalization performance to models trained with first-order optimization methods, but with accelerated convergence. Furthermore, SP-NGD scales to large mini-batch sizes with a negligible computational overhead as compared to first-order methods. We evaluated SP-NGD on a benchmark task where highly optimized first-order methods are available as references: training a ResNet-50 model for image classification on ImageNet. We demonstrate convergence to a top-1 validation accuracy of 75.4% in 5.5 minutes using a mini-batch size of 32,768 with 1,024 GPUs, as well as an accuracy of 74.9% with an extremely large mini-batch size of 131,072 in 873 steps of SP-NGD.

Practical Deep Learning with Bayesian Principles

Bayesian methods promise to fix many shortcomings of deep learning, but they are impractical and rarely match the performance of standard methods, let alone improve them. In this paper, we demonstrate practical training of deep networks with natural-gradient variational inference. By applying techniques such as batch normalisation, data augmentation, and distributed training, we achieve similar performance in about the same number of epochs as the Adam optimiser, even on large datasets such as ImageNet. Importantly, the benefits of Bayesian principles are preserved: predictive probabilities are well-calibrated and uncertainties on out-of-distribution data are improved. This work enables practical deep learning while preserving benefits of Bayesian principles. A PyTorch implementation will be available as a plug-and-play optimiser.

Second-order Optimization Method for Large Mini-batch: Training ResNet-50 on ImageNet in 35 Epochs

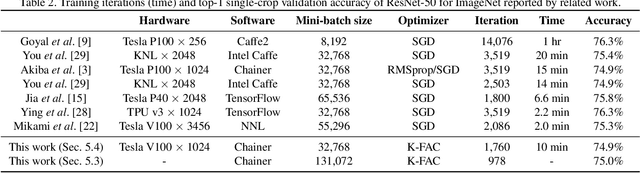
Large-scale distributed training of deep neural networks suffer from the generalization gap caused by the increase in the effective mini-batch size. Previous approaches try to solve this problem by varying the learning rate and batch size over epochs and layers, or some ad hoc modification of the batch normalization. We propose an alternative approach using a second-order optimization method that shows similar generalization capability to first-order methods, but converges faster and can handle larger mini-batches. To test our method on a benchmark where highly optimized first-order methods are available as references, we train ResNet-50 on ImageNet. We converged to 75% Top-1 validation accuracy in 35 epochs for mini-batch sizes under 16,384, and achieved 75% even with a mini-batch size of 131,072, which took 100 epochs.