Optimal Layer Selection for Latent Data Augmentation

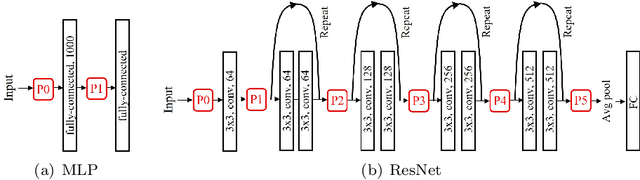
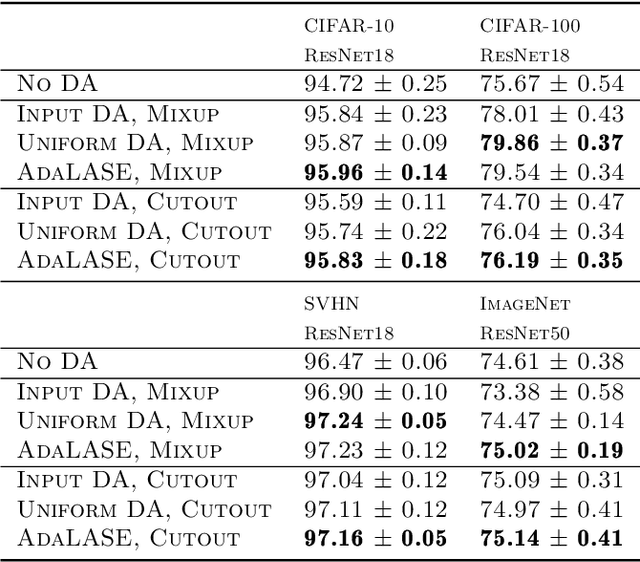
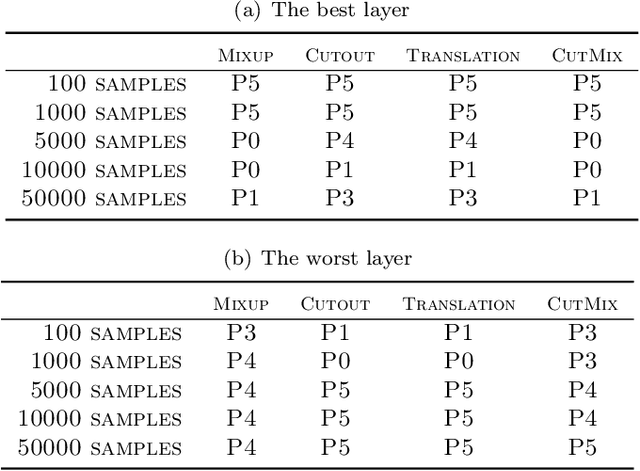
While data augmentation (DA) is generally applied to input data, several studies have reported that applying DA to hidden layers in neural networks, i.e., feature augmentation, can improve performance. However, in previous studies, the layers to which DA is applied have not been carefully considered, often being applied randomly and uniformly or only to a specific layer, leaving room for arbitrariness. Thus, in this study, we investigated the trends of suitable layers for applying DA in various experimental configurations, e.g., training from scratch, transfer learning, various dataset settings, and different models. In addition, to adjust the suitable layers for DA automatically, we propose the adaptive layer selection (AdaLASE) method, which updates the ratio to perform DA for each layer based on the gradient descent method during training. The experimental results obtained on several image classification datasets indicate that the proposed AdaLASE method altered the ratio as expected and achieved high overall test accuracy.

Understanding Gradient Regularization in Deep Learning: Efficient Finite-Difference Computation and Implicit Bias

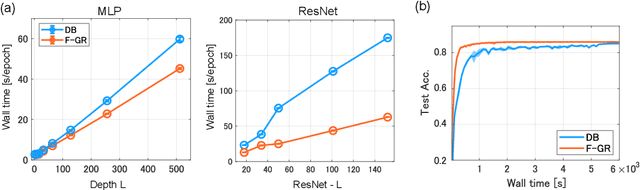
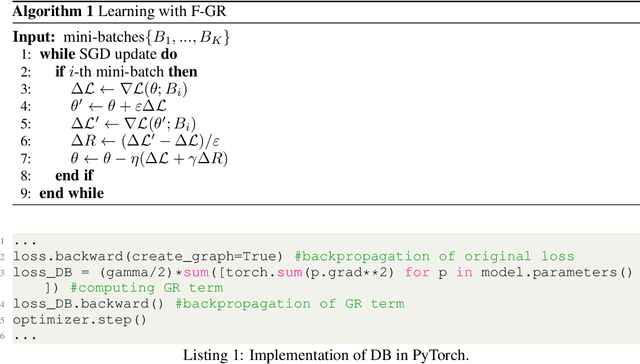
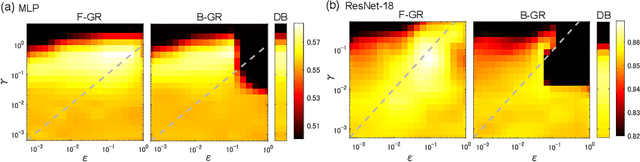
Gradient regularization (GR) is a method that penalizes the gradient norm of the training loss during training. Although some studies have reported that GR improves generalization performance in deep learning, little attention has been paid to it from the algorithmic perspective, that is, the algorithms of GR that efficiently improve performance. In this study, we first reveal that a specific finite-difference computation, composed of both gradient ascent and descent steps, reduces the computational cost for GR. In addition, this computation empirically achieves better generalization performance. Next, we theoretically analyze a solvable model, a diagonal linear network, and clarify that GR has a desirable implicit bias in a certain problem. In particular, learning with the finite-difference GR chooses better minima as the ascent step size becomes larger. Finally, we demonstrate that finite-difference GR is closely related to some other algorithms based on iterative ascent and descent steps for exploring flat minima: sharpness-aware minimization and the flooding method. We reveal that flooding performs finite-difference GR in an implicit way. Thus, this work broadens our understanding of GR in both practice and theory.

Self-paced Data Augmentation for Training Neural Networks

Data augmentation is widely used for machine learning; however, an effective method to apply data augmentation has not been established even though it includes several factors that should be tuned carefully. One such factor is sample suitability, which involves selecting samples that are suitable for data augmentation. A typical method that applies data augmentation to all training samples disregards sample suitability, which may reduce classifier performance. To address this problem, we propose the self-paced augmentation (SPA) to automatically and dynamically select suitable samples for data augmentation when training a neural network. The proposed method mitigates the deterioration of generalization performance caused by ineffective data augmentation. We discuss two reasons the proposed SPA works relative to curriculum learning and desirable changes to loss function instability. Experimental results demonstrate that the proposed SPA can improve the generalization performance, particularly when the number of training samples is small. In addition, the proposed SPA outperforms the state-of-the-art RandAugment method.