Understanding Gradient Regularization in Deep Learning: Efficient Finite-Difference Computation and Implicit Bias
Paper and Code
Oct 06, 2022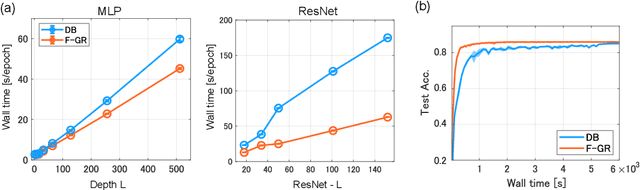
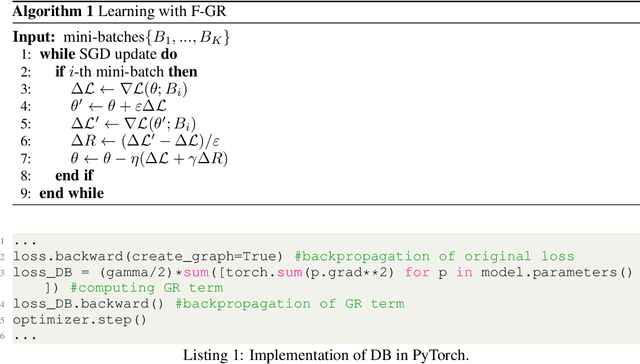

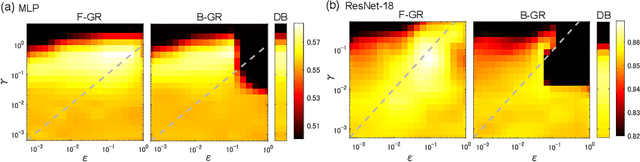
Gradient regularization (GR) is a method that penalizes the gradient norm of the training loss during training. Although some studies have reported that GR improves generalization performance in deep learning, little attention has been paid to it from the algorithmic perspective, that is, the algorithms of GR that efficiently improve performance. In this study, we first reveal that a specific finite-difference computation, composed of both gradient ascent and descent steps, reduces the computational cost for GR. In addition, this computation empirically achieves better generalization performance. Next, we theoretically analyze a solvable model, a diagonal linear network, and clarify that GR has a desirable implicit bias in a certain problem. In particular, learning with the finite-difference GR chooses better minima as the ascent step size becomes larger. Finally, we demonstrate that finite-difference GR is closely related to some other algorithms based on iterative ascent and descent steps for exploring flat minima: sharpness-aware minimization and the flooding method. We reveal that flooding performs finite-difference GR in an implicit way. Thus, this work broadens our understanding of GR in both practice and theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge