PanoTree: Autonomous Photo-Spot Explorer in Virtual Reality Scenes

Social VR platforms enable social, economic, and creative activities by allowing users to create and share their own virtual spaces. In social VR, photography within a VR scene is an important indicator of visitors' activities. Although automatic identification of photo spots within a VR scene can facilitate the process of creating a VR scene and enhance the visitor experience, there are challenges in quantitatively evaluating photos taken in the VR scene and efficiently exploring the large VR scene. We propose PanoTree, an automated photo-spot explorer in VR scenes. To assess the aesthetics of images captured in VR scenes, a deep scoring network is trained on a large dataset of photos collected by a social VR platform to determine whether humans are likely to take similar photos. Furthermore, we propose a Hierarchical Optimistic Optimization (HOO)-based search algorithm to efficiently explore 3D VR spaces with the reward from the scoring network. Our user study shows that the scoring network achieves human-level performance in distinguishing randomly taken images from those taken by humans. In addition, we show applications using the explored photo spots, such as automatic thumbnail generation, support for VR world creation, and visitor flow planning within a VR scene.

MLP-Mixer as a Wide and Sparse MLP

Multi-layer perceptron (MLP) is a fundamental component of deep learning that has been extensively employed for various problems. However, recent empirical successes in MLP-based architectures, particularly the progress of the MLP-Mixer, have revealed that there is still hidden potential in improving MLPs to achieve better performance. In this study, we reveal that the MLP-Mixer works effectively as a wide MLP with certain sparse weights. Initially, we clarify that the mixing layer of the Mixer has an effective expression as a wider MLP whose weights are sparse and represented by the Kronecker product. This expression naturally defines a permuted-Kronecker (PK) family, which can be regarded as a general class of mixing layers and is also regarded as an approximation of Monarch matrices. Subsequently, because the PK family effectively constitutes a wide MLP with sparse weights, one can apply the hypothesis proposed by Golubeva, Neyshabur and Gur-Ari (2021) that the prediction performance improves as the width (sparsity) increases when the number of weights is fixed. We empirically verify this hypothesis by maximizing the effective width of the MLP-Mixer, which enables us to determine the appropriate size of the mixing layers quantitatively.

Understanding Gradient Regularization in Deep Learning: Efficient Finite-Difference Computation and Implicit Bias

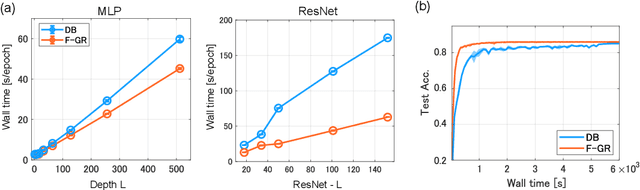
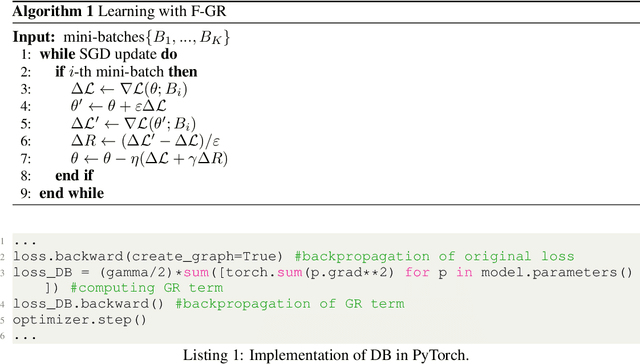
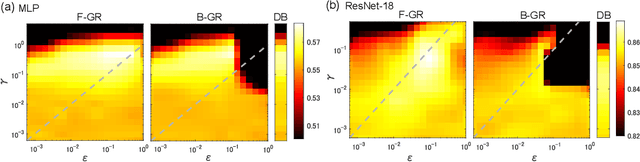
Gradient regularization (GR) is a method that penalizes the gradient norm of the training loss during training. Although some studies have reported that GR improves generalization performance in deep learning, little attention has been paid to it from the algorithmic perspective, that is, the algorithms of GR that efficiently improve performance. In this study, we first reveal that a specific finite-difference computation, composed of both gradient ascent and descent steps, reduces the computational cost for GR. In addition, this computation empirically achieves better generalization performance. Next, we theoretically analyze a solvable model, a diagonal linear network, and clarify that GR has a desirable implicit bias in a certain problem. In particular, learning with the finite-difference GR chooses better minima as the ascent step size becomes larger. Finally, we demonstrate that finite-difference GR is closely related to some other algorithms based on iterative ascent and descent steps for exploring flat minima: sharpness-aware minimization and the flooding method. We reveal that flooding performs finite-difference GR in an implicit way. Thus, this work broadens our understanding of GR in both practice and theory.

Asymptotic Freeness of Layerwise Jacobians Caused by Invariance of Multilayer Perceptron: The Haar Orthogonal Case

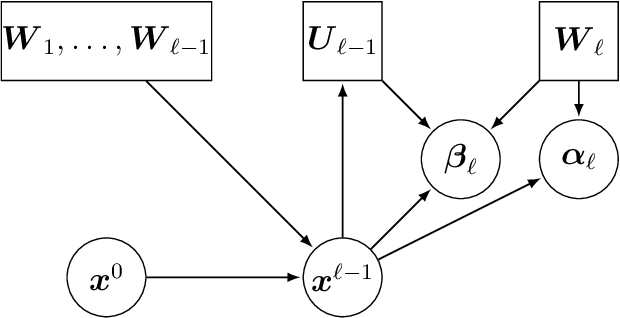
Free Probability Theory (FPT) provides rich knowledge for handling mathematical difficulties caused by random matrices that appear in research related to deep neural networks (DNNs), such as the dynamical isometry, Fisher information matrix, and training dynamics. FPT suits these researches because the DNN's parameter-Jacobian and input-Jacobian are polynomials of layerwise Jacobians. However, the critical assumption of asymptotic freenss of the layerwise Jacobian has not been proven completely so far. The asymptotic freeness assumption plays a fundamental role when propagating spectral distributions through the layers. Haar distributed orthogonal matrices are essential for achieving dynamical isometry. In this work, we prove asymptotic freeness of layerwise Jacobian of multilayer perceptrons in this case.

Layer-Wise Interpretation of Deep Neural Networks Using Identity Initialization

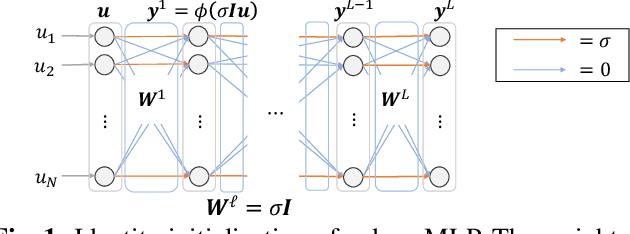
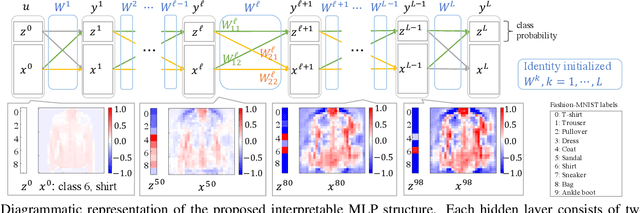
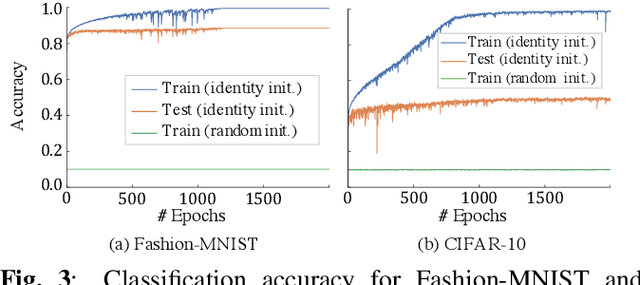
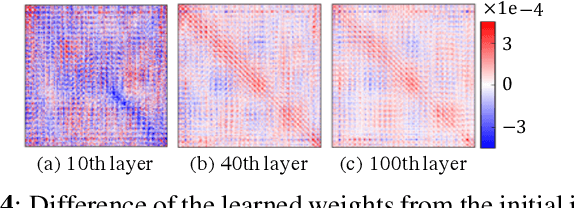
The interpretability of neural networks (NNs) is a challenging but essential topic for transparency in the decision-making process using machine learning. One of the reasons for the lack of interpretability is random weight initialization, where the input is randomly embedded into a different feature space in each layer. In this paper, we propose an interpretation method for a deep multilayer perceptron, which is the most general architecture of NNs, based on identity initialization (namely, initialization using identity matrices). The proposed method allows us to analyze the contribution of each neuron to classification and class likelihood in each hidden layer. As a property of the identity-initialized perceptron, the weight matrices remain near the identity matrices even after learning. This property enables us to treat the change of features from the input to each hidden layer as the contribution to classification. Furthermore, we can separate the output of each hidden layer into a contribution map that depicts the contribution to classification and class likelihood, by adding extra dimensions to each layer according to the number of classes, thereby allowing the calculation of the recognition accuracy in each layer and thus revealing the roles of independent layers, such as feature extraction and classification.

Selective Forgetting of Deep Networks at a Finer Level than Samples

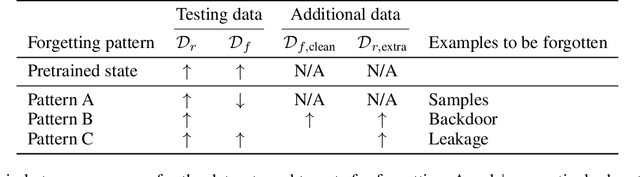
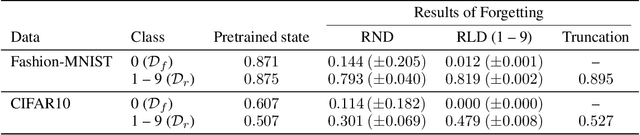
Selective forgetting or removing information from deep neural networks (DNNs) is essential for continual learning and is challenging in controlling the DNNs. Such forgetting is crucial also in a practical sense since the deployed DNNs may be trained on the data with outliers, poisoned by attackers, or with leaked/sensitive information. In this paper, we formulate selective forgetting for classification tasks at a finer level than the samples' level. We specify the finer level based on four datasets distinguished by two conditions: whether they contain information to be forgotten and whether they are available for the forgetting procedure. Additionally, we reveal the need for such formulation with the datasets by showing concrete and practical situations. Moreover, we introduce the forgetting procedure as an optimization problem on three criteria; the forgetting, the correction, and the remembering term. Experimental results show that the proposed methods can make the model forget to use specific information for classification. Notably, in specific cases, our methods improved the model's accuracy on the datasets, which contains information to be forgotten but is unavailable in the forgetting procedure. Such data are unexpectedly found and misclassified in actual situations.

The Spectrum of Fisher Information of Deep Networks Achieving Dynamical Isometry

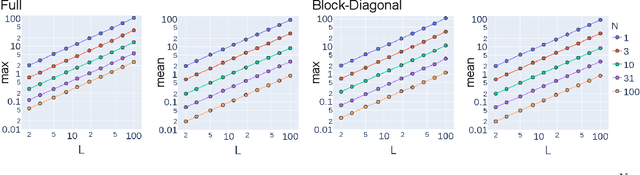
The Fisher information matrix (FIM) is fundamental for understanding the trainability of deep neural networks (DNN) since it describes the local metric of the parameter space. We investigate the spectral distribution of the FIM given a single input by focusing on fully-connected networks achieving dynamical isometry. Then, while dynamical isometry is known to keep specific backpropagated signals independent of the depth, we find that the parameter space's local metric depends on the depth. In particular, we obtain an exact expression of the spectrum of the FIM given a single input and reveal that it concentrates around the depth point. Here, considering random initialization and the wide limit, we construct an algebraic methodology to examine the spectrum based on free probability theory, which is the algebraic wrapper of random matrix theory. As a byproduct, we provide the solvable spectral distribution in the two-hidden-layer case. Lastly, we empirically confirm that the spectrum of FIM with small batch-size has the same property as the single-input version. An experimental result shows that FIM's dependence on the depth determines the appropriate size of the learning rate for convergence at the initial phase of the online training of DNNs.

Almost Surely Asymptotic Freeness for Jacobian Spectrum of Deep Network

Free probability theory helps us to understand Jacobian spectrum of deep neural networks. We rigorously show almost surely asymptotic freeness of layer-wise Jacobians.

Cauchy noise loss for stochastic optimization of random matrix models via free deterministic equivalents

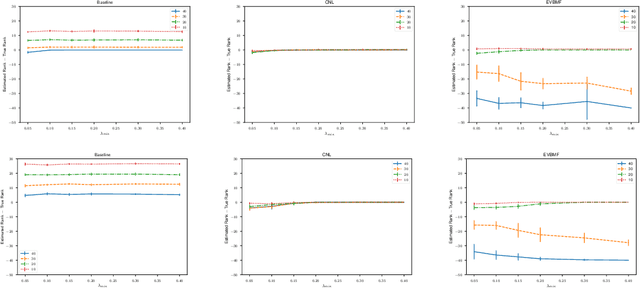
For random matrix models, the parameter estimation based on the traditional likelihood is not straightforward in particular when there is only one sample matrix. We introduce a new parameter optimization method of random matrix models which works even in such a case not based on the traditional likelihood, instead based on the spectral distribution. We use the spectral distribution perturbed by Cauchy noises because the free deterministic equivalent, which is a tool in free probability theory, allows us to approximate it by a smooth and accessible density function. Moreover, we study an asymptotic property of a determination gap, which has a similar role as the generalization gap. In addition, we propose a new dimensionality recovery method for the signal-plus-noise model, and experimentally demonstrate that it recovers the rank of the signal part even if the rank is not low. It is a simultaneous rank selection and parameter estimation procedure.