Free Random Projection for In-Context Reinforcement Learning

Hierarchical inductive biases are hypothesized to promote generalizable policies in reinforcement learning, as demonstrated by explicit hyperbolic latent representations and architectures. Therefore, a more flexible approach is to have these biases emerge naturally from the algorithm. We introduce Free Random Projection, an input mapping grounded in free probability theory that constructs random orthogonal matrices where hierarchical structure arises inherently. The free random projection integrates seamlessly into existing in-context reinforcement learning frameworks by encoding hierarchical organization within the input space without requiring explicit architectural modifications. Empirical results on multi-environment benchmarks show that free random projection consistently outperforms the standard random projection, leading to improvements in generalization. Furthermore, analyses within linearly solvable Markov decision processes and investigations of the spectrum of kernel random matrices reveal the theoretical underpinnings of free random projection's enhanced performance, highlighting its capacity for effective adaptation in hierarchically structured state spaces.

Universal consistency of the $k$-NN rule in metric spaces and Nagata dimension

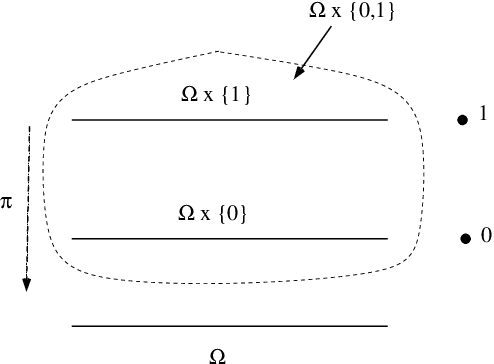
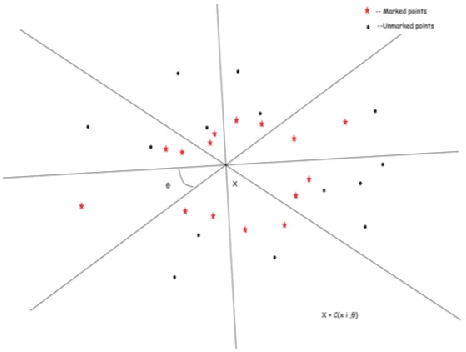
The $k$ nearest neighbour learning rule (under the uniform distance tie breaking) is universally consistent in every metric space $X$ that is sigma-finite dimensional in the sense of Nagata. This was pointed out by C\'erou and Guyader (2006) as a consequence of the main result by those authors, combined with a theorem in real analysis sketched by D. Preiss (1971) (and elaborated in detail by Assouad and Quentin de Gromard (2006)). We show that it is possible to give a direct proof along the same lines as the original theorem of Charles J. Stone (1977) about the universal consistency of the $k$-NN classifier in the finite dimensional Euclidean space. The generalization is non-trivial because of the distance ties being more prevalent in the non-euclidean setting, and on the way we investigate the relevant geometric properties of the metrics and the limitations of the Stone argument, by constructing various examples.