Universal consistency of the $k$-NN rule in metric spaces and Nagata dimension. II

We continue to investigate the $k$ nearest neighbour learning rule in separable metric spaces. Thanks to the results of C\'erou and Guyader (2006) and Preiss (1983), this rule is known to be universally consistent in every metric space $X$ that is sigma-finite dimensional in the sense of Nagata. Here we show that the rule is strongly universally consistent in such spaces in the absence of ties. Under the tie-breaking strategy applied by Devroye, Gy\"{o}rfi, Krzy\.{z}ak, and Lugosi (1994) in the Euclidean setting, we manage to show the strong universal consistency in non-Archimedian metric spaces (that is, those of Nagata dimension zero). Combining the theorem of C\'erou and Guyader with results of Assouad and Quentin de Gromard (2006), one deduces that the $k$-NN rule is universally consistent in metric spaces having finite dimension in the sense of de Groot. In particular, the $k$-NN rule is universally consistent in the Heisenberg group which is not sigma-finite dimensional in the sense of Nagata as follows from an example independently constructed by Kor\'anyi and Reimann (1995) and Sawyer and Wheeden (1992).

A learning problem whose consistency is equivalent to the non-existence of real-valued measurable cardinals

We show that the $k$-nearest neighbour learning rule is universally consistent in a metric space $X$ if and only if it is universally consistent in every separable subspace of $X$ and the density of $X$ is less than every real-measurable cardinal. In particular, the $k$-NN classifier is universally consistent in every metric space whose separable subspaces are sigma-finite dimensional in the sense of Nagata and Preiss if and only if there are no real-valued measurable cardinals. The latter assumption is relatively consistent with ZFC, however the consistency of the existence of such cardinals cannot be proved within ZFC. Our results were inspired by an example sketched by C\'erou and Guyader in 2006 at an intuitive level of rigour.

Universal consistency of the $k$-NN rule in metric spaces and Nagata dimension

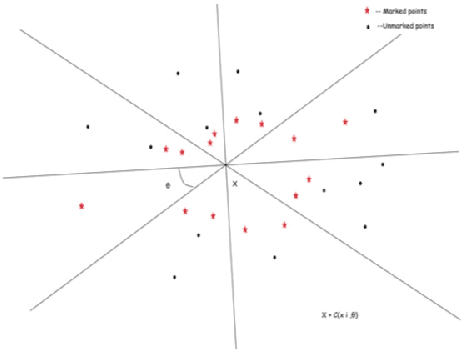
The $k$ nearest neighbour learning rule (under the uniform distance tie breaking) is universally consistent in every metric space $X$ that is sigma-finite dimensional in the sense of Nagata. This was pointed out by C\'erou and Guyader (2006) as a consequence of the main result by those authors, combined with a theorem in real analysis sketched by D. Preiss (1971) (and elaborated in detail by Assouad and Quentin de Gromard (2006)). We show that it is possible to give a direct proof along the same lines as the original theorem of Charles J. Stone (1977) about the universal consistency of the $k$-NN classifier in the finite dimensional Euclidean space. The generalization is non-trivial because of the distance ties being more prevalent in the non-euclidean setting, and on the way we investigate the relevant geometric properties of the metrics and the limitations of the Stone argument, by constructing various examples.

Elementos da teoria de aprendizagem de máquina supervisionada

This is a set of lecture notes for an introductory course (advanced undergaduates or the 1st graduate course) on foundations of supervised machine learning (in Portuguese). The topics include: the geometry of the Hamming cube, concentration of measure, shattering and VC dimension, Glivenko-Cantelli classes, PAC learnability, universal consistency and the k-NN classifier in metric spaces, dimensionality reduction, universal approximation, sample compression. There are appendices on metric and normed spaces, measure theory, etc., making the notes self-contained. Este \'e um conjunto de notas de aula para um curso introdut\'orio (curso de gradua\c{c}\~ao avan\c{c}ado ou o 1o curso de p\'os) sobre fundamentos da aprendizagem de m\'aquina supervisionada (em Portugu\^es). Os t\'opicos incluem: a geometria do cubo de Hamming, concentra\c{c}\~ao de medida, fragmenta\c{c}\~ao e dimens\~ao de Vapnik-Chervonenkis, classes de Glivenko-Cantelli, aprendizabilidade PAC, consist\^encia universal e o classificador k-NN em espa\c{c}os m\'etricos, redu\c{c}\~ao de dimensionalidade, aproxima\c{c}\~ao universal, compress\~ao amostral. H\'a ap\^endices sobre espa\c{c}os m\'etricos e normados, teoria de medida, etc., tornando as notas autosuficientes.