Universal consistency of the $k$-NN rule in metric spaces and Nagata dimension. II

We continue to investigate the $k$ nearest neighbour learning rule in separable metric spaces. Thanks to the results of C\'erou and Guyader (2006) and Preiss (1983), this rule is known to be universally consistent in every metric space $X$ that is sigma-finite dimensional in the sense of Nagata. Here we show that the rule is strongly universally consistent in such spaces in the absence of ties. Under the tie-breaking strategy applied by Devroye, Gy\"{o}rfi, Krzy\.{z}ak, and Lugosi (1994) in the Euclidean setting, we manage to show the strong universal consistency in non-Archimedian metric spaces (that is, those of Nagata dimension zero). Combining the theorem of C\'erou and Guyader with results of Assouad and Quentin de Gromard (2006), one deduces that the $k$-NN rule is universally consistent in metric spaces having finite dimension in the sense of de Groot. In particular, the $k$-NN rule is universally consistent in the Heisenberg group which is not sigma-finite dimensional in the sense of Nagata as follows from an example independently constructed by Kor\'anyi and Reimann (1995) and Sawyer and Wheeden (1992).

NoFake at CheckThat! 2021: Fake News Detection Using BERT

Much research has been done for debunking and analysing fake news. Many researchers study fake news detection in the last year, but many are limited to social media data. Currently, multiples fact-checkers are publishing their results in various formats. Also, multiple fact-checkers use different labels for the fake news, making it difficult to make a generalisable classifier. With the merge classes, the performance of the machine model can be enhanced. This domain categorisation will help group the article, which will help save the manual effort in assigning the claim verification. In this paper, we have presented BERT based classification model to predict the domain and classification. We have also used additional data from fact-checked articles. We have achieved a macro F1 score of 83.76 % for Task 3Aand 85.55 % for Task 3B using the additional training data.

Universal consistency of the $k$-NN rule in metric spaces and Nagata dimension

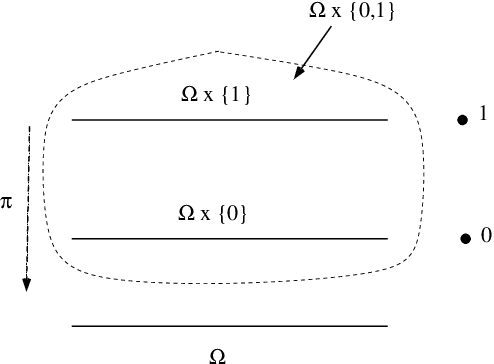
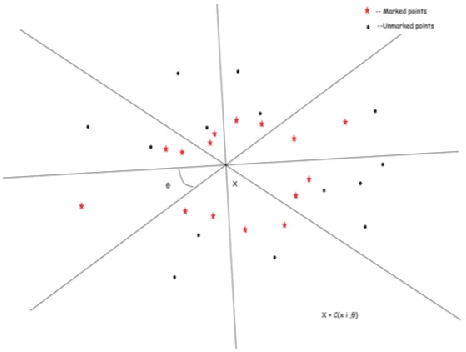
The $k$ nearest neighbour learning rule (under the uniform distance tie breaking) is universally consistent in every metric space $X$ that is sigma-finite dimensional in the sense of Nagata. This was pointed out by C\'erou and Guyader (2006) as a consequence of the main result by those authors, combined with a theorem in real analysis sketched by D. Preiss (1971) (and elaborated in detail by Assouad and Quentin de Gromard (2006)). We show that it is possible to give a direct proof along the same lines as the original theorem of Charles J. Stone (1977) about the universal consistency of the $k$-NN classifier in the finite dimensional Euclidean space. The generalization is non-trivial because of the distance ties being more prevalent in the non-euclidean setting, and on the way we investigate the relevant geometric properties of the metrics and the limitations of the Stone argument, by constructing various examples.

Topics in Random Matrices and Statistical Machine Learning

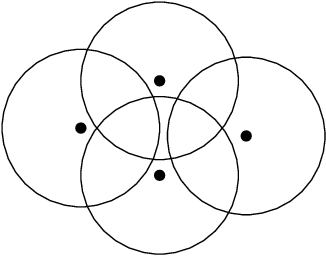
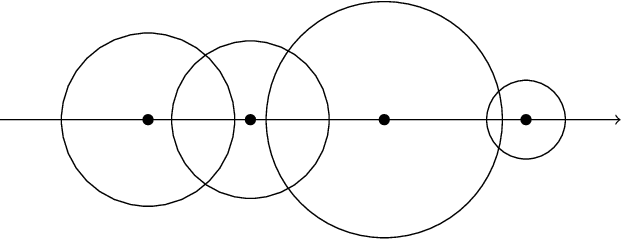
This thesis consists of two independent parts: random matrices, which form the first one-third of this thesis, and machine learning, which constitutes the remaining part. The main results of this thesis are as follows: a necessary and sufficient condition for the inverse moments of $(m,n,\beta)$-Laguerre matrices and compound Wishart matrices to be finite; the universal weak consistency and the strong consistency of the $k$-nearest neighbor rule in metrically sigma-finite dimensional spaces and metrically finite dimensional spaces respectively. In Part I, the Chapter 1 introduces the $(m,n,\beta)$-Laguerre matrix, Wishart and compound Wishart matrix and their joint eigenvalue distribution. While in Chapter 2, a necessary and sufficient condition to have finite inverse moments has been derived. In Part II, the Chapter 1 introduces the various notions of metric dimension and differentiation property followed by our proof for the necessary part of Preiss' result. Further, Chapter 2 gives an introduction to the mathematical concepts in statistical machine learning and then the $k$-nearest neighbor rule is presented in Chapter 3 with a proof of Stone's theorem. In chapters 4 and 5, we present our main results and some possible future directions based on it.