Cauchy noise loss for stochastic optimization of random matrix models via free deterministic equivalents
Paper and Code
Aug 05, 2018

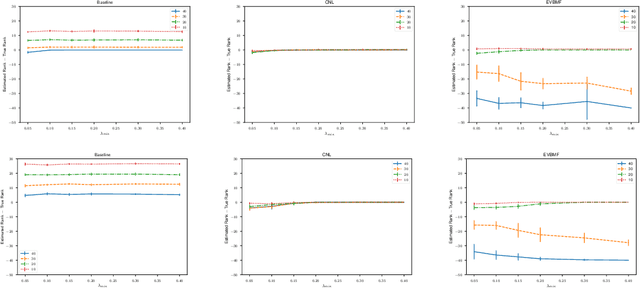

For random matrix models, the parameter estimation based on the traditional likelihood is not straightforward in particular when there is only one sample matrix. We introduce a new parameter optimization method of random matrix models which works even in such a case not based on the traditional likelihood, instead based on the spectral distribution. We use the spectral distribution perturbed by Cauchy noises because the free deterministic equivalent, which is a tool in free probability theory, allows us to approximate it by a smooth and accessible density function. Moreover, we study an asymptotic property of a determination gap, which has a similar role as the generalization gap. In addition, we propose a new dimensionality recovery method for the signal-plus-noise model, and experimentally demonstrate that it recovers the rank of the signal part even if the rank is not low. It is a simultaneous rank selection and parameter estimation procedure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge