The Spectrum of Fisher Information of Deep Networks Achieving Dynamical Isometry
Paper and Code
Jul 07, 2020

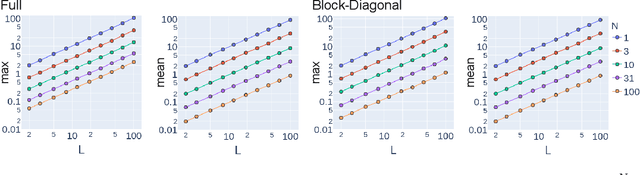

The Fisher information matrix (FIM) is fundamental for understanding the trainability of deep neural networks (DNN) since it describes the local metric of the parameter space. We investigate the spectral distribution of the FIM given a single input by focusing on fully-connected networks achieving dynamical isometry. Then, while dynamical isometry is known to keep specific backpropagated signals independent of the depth, we find that the parameter space's local metric depends on the depth. In particular, we obtain an exact expression of the spectrum of the FIM given a single input and reveal that it concentrates around the depth point. Here, considering random initialization and the wide limit, we construct an algebraic methodology to examine the spectrum based on free probability theory, which is the algebraic wrapper of random matrix theory. As a byproduct, we provide the solvable spectral distribution in the two-hidden-layer case. Lastly, we empirically confirm that the spectrum of FIM with small batch-size has the same property as the single-input version. An experimental result shows that FIM's dependence on the depth determines the appropriate size of the learning rate for convergence at the initial phase of the online training of DNNs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge