Layer-Wise Interpretation of Deep Neural Networks Using Identity Initialization
Paper and Code
Feb 26, 2021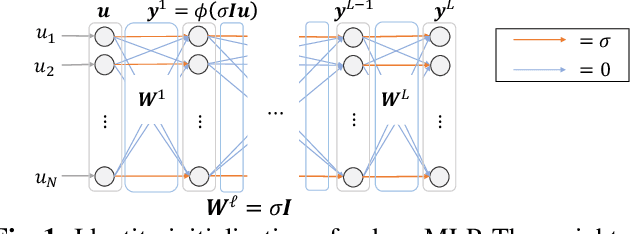
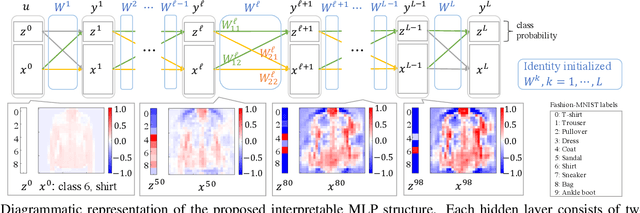
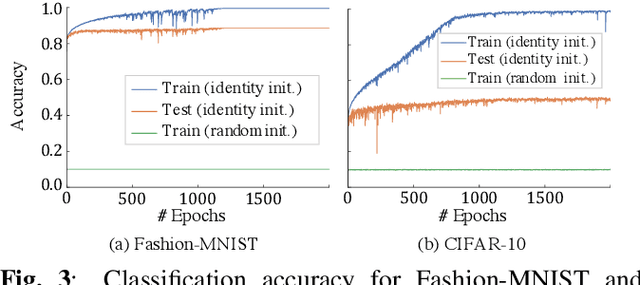
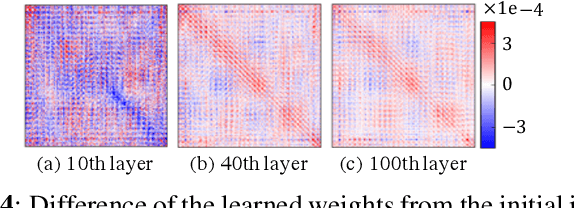
The interpretability of neural networks (NNs) is a challenging but essential topic for transparency in the decision-making process using machine learning. One of the reasons for the lack of interpretability is random weight initialization, where the input is randomly embedded into a different feature space in each layer. In this paper, we propose an interpretation method for a deep multilayer perceptron, which is the most general architecture of NNs, based on identity initialization (namely, initialization using identity matrices). The proposed method allows us to analyze the contribution of each neuron to classification and class likelihood in each hidden layer. As a property of the identity-initialized perceptron, the weight matrices remain near the identity matrices even after learning. This property enables us to treat the change of features from the input to each hidden layer as the contribution to classification. Furthermore, we can separate the output of each hidden layer into a contribution map that depicts the contribution to classification and class likelihood, by adding extra dimensions to each layer according to the number of classes, thereby allowing the calculation of the recognition accuracy in each layer and thus revealing the roles of independent layers, such as feature extraction and classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge