The ParClusterers Benchmark Suite (PCBS): A Fine-Grained Analysis of Scalable Graph Clustering

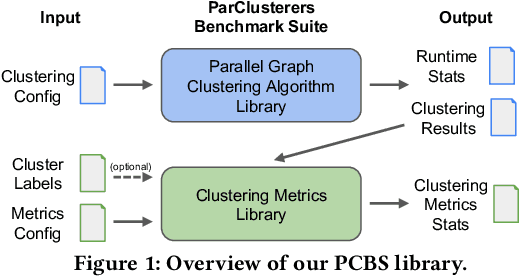
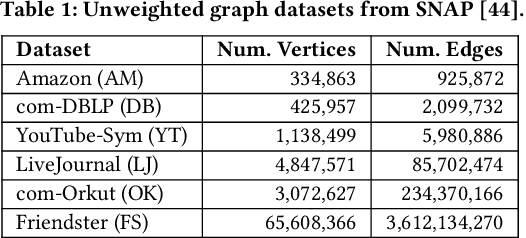
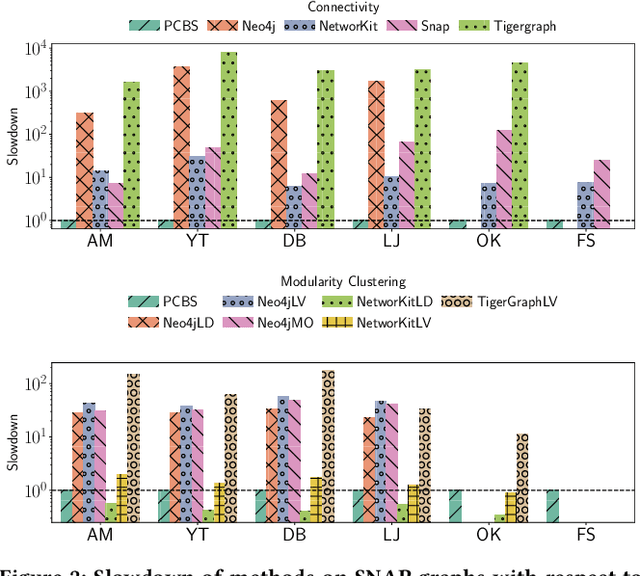
We introduce the ParClusterers Benchmark Suite (PCBS) -- a collection of highly scalable parallel graph clustering algorithms and benchmarking tools that streamline comparing different graph clustering algorithms and implementations. The benchmark includes clustering algorithms that target a wide range of modern clustering use cases, including community detection, classification, and dense subgraph mining. The benchmark toolkit makes it easy to run and evaluate multiple instances of different clustering algorithms, which can be useful for fine-tuning the performance of clustering on a given task, and for comparing different clustering algorithms based on different metrics of interest, including clustering quality and running time. Using PCBS, we evaluate a broad collection of real-world graph clustering datasets. Somewhat surprisingly, we find that the best quality results are obtained by algorithms that not included in many popular graph clustering toolkits. The PCBS provides a standardized way to evaluate and judge the quality-performance tradeoffs of the active research area of scalable graph clustering algorithms. We believe it will help enable fair, accurate, and nuanced evaluation of graph clustering algorithms in the future.

When Heterophily Meets Heterogeneity: New Graph Benchmarks and Effective Methods

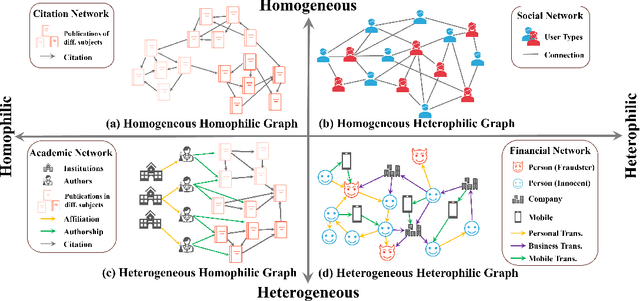
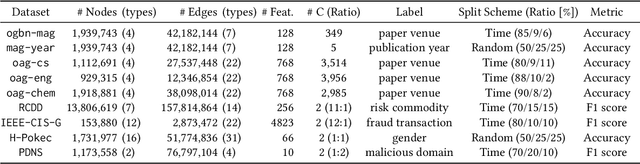
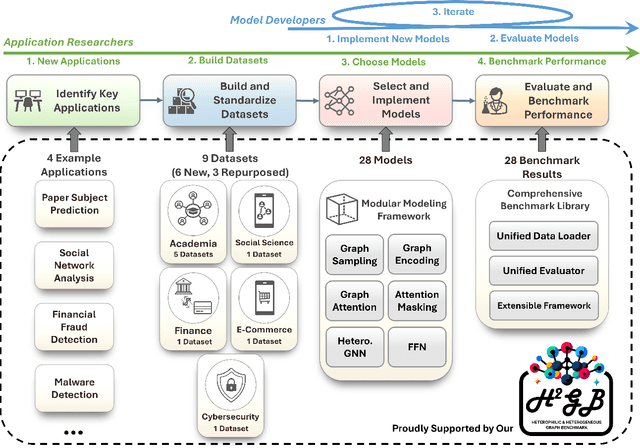
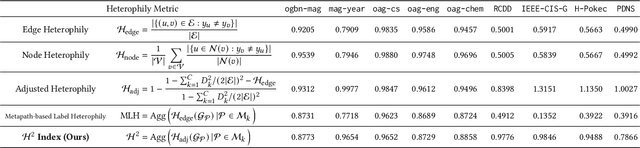
Many real-world graphs frequently present challenges for graph learning due to the presence of both heterophily and heterogeneity. However, existing benchmarks for graph learning often focus on heterogeneous graphs with homophily or homogeneous graphs with heterophily, leaving a gap in understanding how methods perform on graphs that are both heterogeneous and heterophilic. To bridge this gap, we introduce H2GB, a novel graph benchmark that brings together the complexities of both the heterophily and heterogeneity properties of graphs. Our benchmark encompasses 9 diverse real-world datasets across 5 domains, 28 baseline model implementations, and 26 benchmark results. In addition, we present a modular graph transformer framework UnifiedGT and a new model variant, H2G-former, that excels at this challenging benchmark. By integrating masked label embeddings, cross-type heterogeneous attention, and type-specific FFNs, H2G-former effectively tackles graph heterophily and heterogeneity. Extensive experiments across 26 baselines on H2GB reveal inadequacies of current models on heterogeneous heterophilic graph learning, and demonstrate the superiority of our H2G-former over existing solutions. Both the benchmark and the framework are available on GitHub (https://github.com/junhongmit/H2GB) and PyPI (https://pypi.org/project/H2GB), and documentation can be found at https://junhongmit.github.io/H2GB/.

Approximate Nearest Neighbor Search with Window Filters

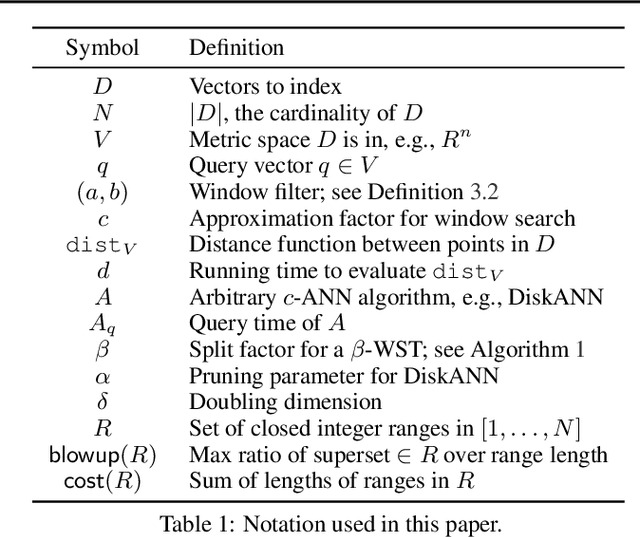
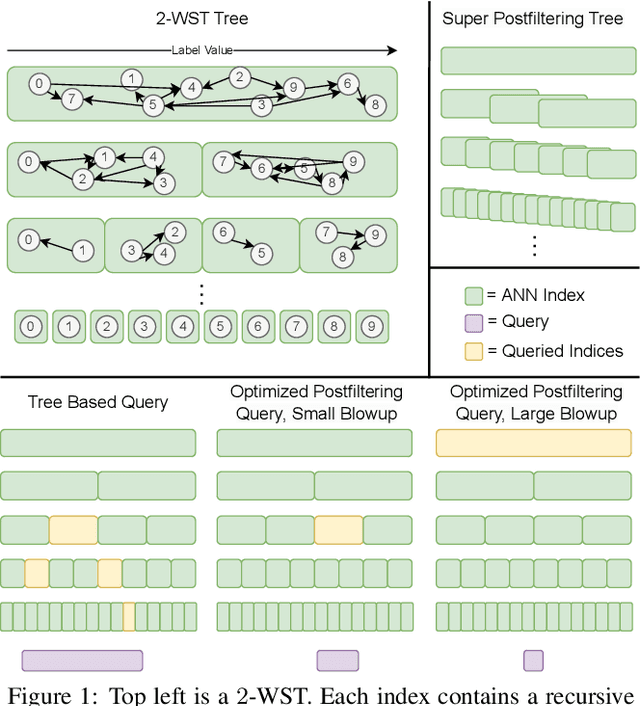
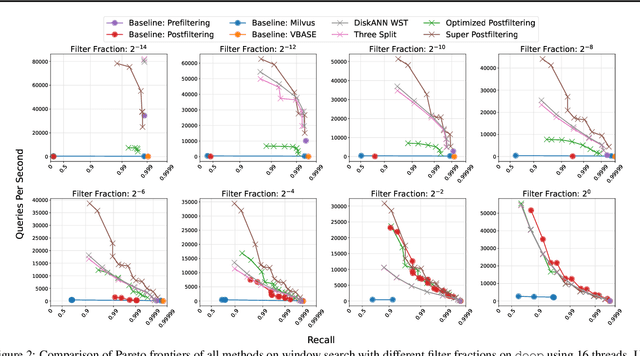
We define and investigate the problem of $\textit{c-approximate window search}$: approximate nearest neighbor search where each point in the dataset has a numeric label, and the goal is to find nearest neighbors to queries within arbitrary label ranges. Many semantic search problems, such as image and document search with timestamp filters, or product search with cost filters, are natural examples of this problem. We propose and theoretically analyze a modular tree-based framework for transforming an index that solves the traditional c-approximate nearest neighbor problem into a data structure that solves window search. On standard nearest neighbor benchmark datasets equipped with random label values, adversarially constructed embeddings, and image search embeddings with real timestamps, we obtain up to a $75\times$ speedup over existing solutions at the same level of recall.

PECANN: Parallel Efficient Clustering with Graph-Based Approximate Nearest Neighbor Search

This paper studies density-based clustering of point sets. These methods use dense regions of points to detect clusters of arbitrary shapes. In particular, we study variants of density peaks clustering, a popular type of algorithm that has been shown to work well in practice. Our goal is to cluster large high-dimensional datasets, which are prevalent in practice. Prior solutions are either sequential, and cannot scale to large data, or are specialized for low-dimensional data. This paper unifies the different variants of density peaks clustering into a single framework, PECANN, by abstracting out several key steps common to this class of algorithms. One such key step is to find nearest neighbors that satisfy a predicate function, and one of the main contributions of this paper is an efficient way to do this predicate search using graph-based approximate nearest neighbor search (ANNS). To provide ample parallelism, we propose a doubling search technique that enables points to find an approximate nearest neighbor satisfying the predicate in a small number of rounds. Our technique can be applied to many existing graph-based ANNS algorithms, which can all be plugged into PECANN. We implement five clustering algorithms with PECANN and evaluate them on synthetic and real-world datasets with up to 1.28 million points and up to 1024 dimensions on a 30-core machine with two-way hyper-threading. Compared to the state-of-the-art FASTDP algorithm for high-dimensional density peaks clustering, which is sequential, our best algorithm is 45x-734x faster while achieving competitive ARI scores. Compared to the state-of-the-art parallel DPC-based algorithm, which is optimized for low dimensions, we show that PECANN is two orders of magnitude faster. As far as we know, our work is the first to evaluate DPC variants on large high-dimensional real-world image and text embedding datasets.

ParChain: A Framework for Parallel Hierarchical Agglomerative Clustering using Nearest-Neighbor Chain

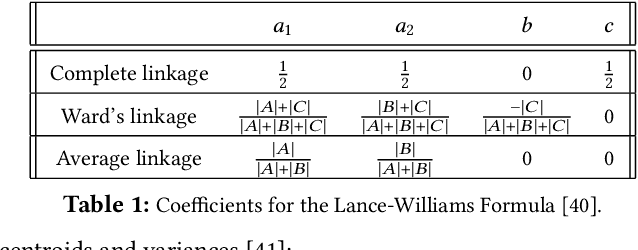
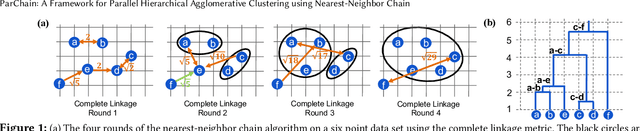
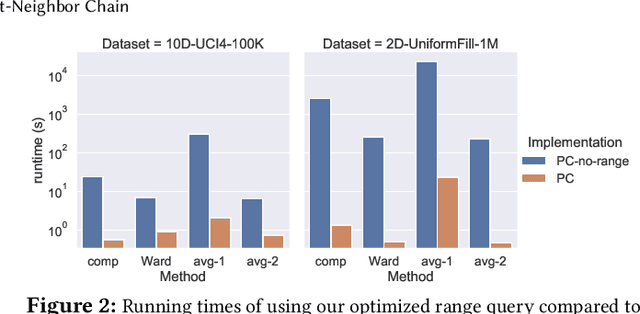
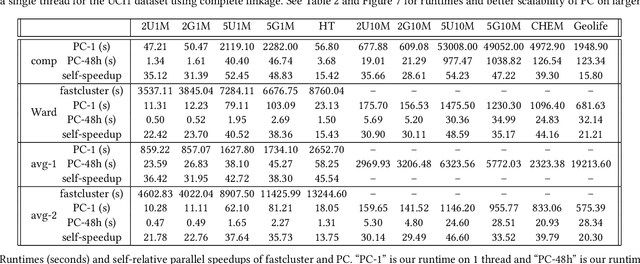
This paper studies the hierarchical clustering problem, where the goal is to produce a dendrogram that represents clusters at varying scales of a data set. We propose the ParChain framework for designing parallel hierarchical agglomerative clustering (HAC) algorithms, and using the framework we obtain novel parallel algorithms for the complete linkage, average linkage, and Ward's linkage criteria. Compared to most previous parallel HAC algorithms, which require quadratic memory, our new algorithms require only linear memory, and are scalable to large data sets. ParChain is based on our parallelization of the nearest-neighbor chain algorithm, and enables multiple clusters to be merged on every round. We introduce two key optimizations that are critical for efficiency: a range query optimization that reduces the number of distance computations required when finding nearest neighbors of clusters, and a caching optimization that stores a subset of previously computed distances, which are likely to be reused. Experimentally, we show that our highly-optimized implementations using 48 cores with two-way hyper-threading achieve 5.8--110.1x speedup over state-of-the-art parallel HAC algorithms and achieve 13.75--54.23x self-relative speedup. Compared to state-of-the-art algorithms, our algorithms require up to 237.3x less space. Our algorithms are able to scale to data set sizes with tens of millions of points, which existing algorithms are not able to handle.

Fast Parallel Algorithms for Euclidean Minimum Spanning Tree and Hierarchical Spatial Clustering

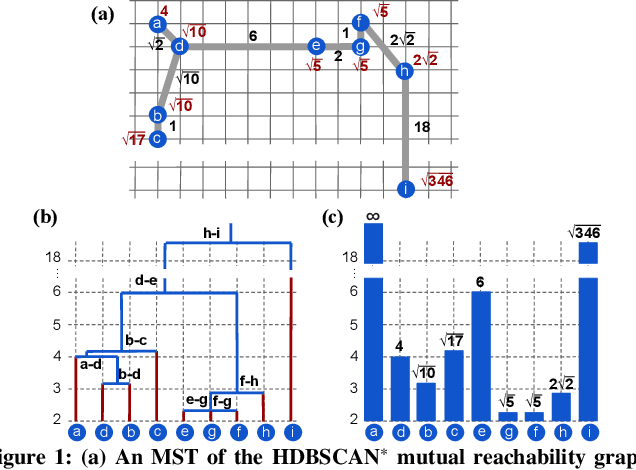
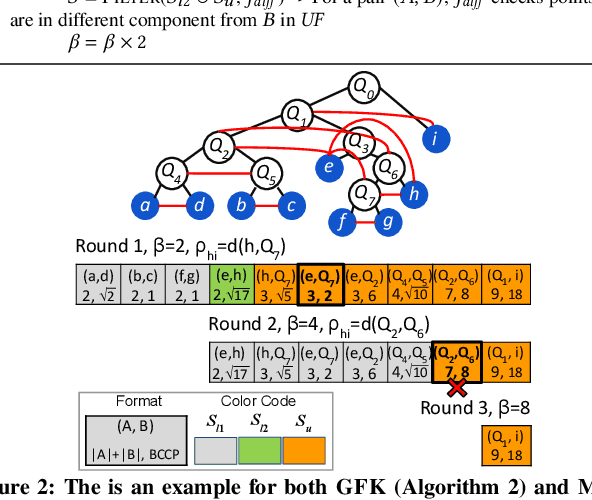
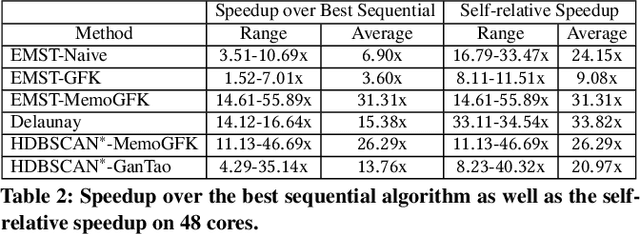
This paper presents new parallel algorithms for generating Euclidean minimum spanning trees and spatial clustering hierarchies (known as HDBSCAN$^*$). Our approach is based on generating a well-separated pair decomposition followed by using Kruskal's minimum spanning tree algorithm and bichromatic closest pair computations. We introduce a new notion of well-separation to reduce the work and space of our algorithm for HDBSCAN$^*$. We also present a parallel approximate algorithm for OPTICS based on a recent sequential algorithm by Gan and Tao. Finally, we give a new parallel divide-and-conquer algorithm for computing the dendrogram and reachability plots, which are used in visualizing clusters of different scale that arise for both EMST and HDBSCAN$^*$. We show that our algorithms are theoretically efficient: they have work (number of operations) matching their sequential counterparts, and polylogarithmic depth (parallel time). We implement our algorithms and propose a memory optimization that requires only a subset of well-separated pairs to be computed and materialized, leading to savings in both space (up to 10x) and time (up to 8x). Our experiments on large real-world and synthetic data sets using a 48-core machine show that our fastest algorithms outperform the best serial algorithms for the problems by 11.13--55.89x, and existing parallel algorithms by at least an order of magnitude.

Theoretically-Efficient and Practical Parallel DBSCAN

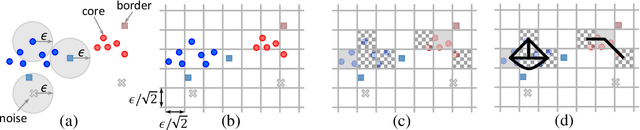
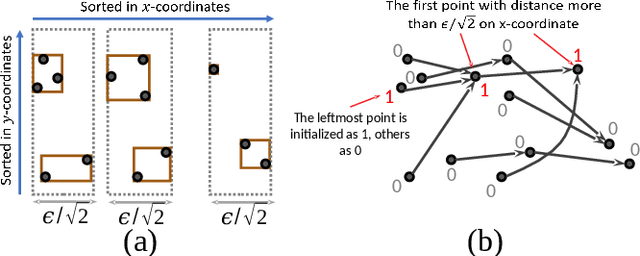
The DBSCAN method for spatial clustering has received significant attention due to its applicability in a variety of data analysis tasks. There are fast sequential algorithms for DBSCAN in Euclidean space that take $O(n\log n)$ work for two dimensions, sub-quadratic work for three or more dimensions, and can be computed approximately in linear work for any constant number of dimensions. However, existing parallel DBSCAN algorithms require quadratic work in the worst case, making them inefficient for large datasets. This paper bridges the gap between theory and practice of parallel DBSCAN by presenting new parallel algorithms for Euclidean exact DBSCAN and approximate DBSCAN that match the work bounds of their sequential counterparts, and are highly parallel (polylogarithmic depth). We present implementations of our algorithms along with optimizations that improve their practical performance. We perform a comprehensive experimental evaluation of our algorithms on a variety of datasets and parameter settings. Our experiments on a 36-core machine with hyper-threading show that we outperform existing parallel DBSCAN implementations by up to several orders of magnitude, and achieve speedups by up to 33x over the best sequential algorithms.