Chamfer-Linkage for Hierarchical Agglomerative Clustering

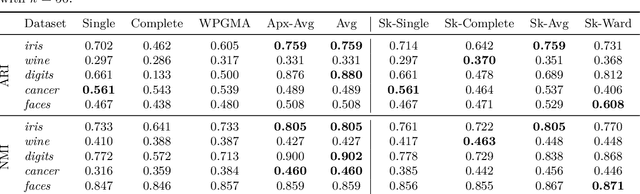
Hierarchical Agglomerative Clustering (HAC) is a widely-used clustering method based on repeatedly merging the closest pair of clusters, where inter-cluster distances are determined by a linkage function. Unlike many clustering methods, HAC does not optimize a single explicit global objective; clustering quality is therefore primarily evaluated empirically, and the choice of linkage function plays a crucial role in practice. However, popular classical linkages, such as single-linkage, average-linkage and Ward's method show high variability across real-world datasets and do not consistently produce high-quality clusterings in practice. In this paper, we propose \emph{Chamfer-linkage}, a novel linkage function that measures the distance between clusters using the Chamfer distance, a popular notion of distance between point-clouds in machine learning and computer vision. We argue that Chamfer-linkage satisfies desirable concept representation properties that other popular measures struggle to satisfy. Theoretically, we show that Chamfer-linkage HAC can be implemented in $O(n^2)$ time, matching the efficiency of classical linkage functions. Experimentally, we find that Chamfer-linkage consistently yields higher-quality clusterings than classical linkages such as average-linkage and Ward's method across a diverse collection of datasets. Our results establish Chamfer-linkage as a practical drop-in replacement for classical linkage functions, broadening the toolkit for hierarchical clustering in both theory and practice.

JAG: Joint Attribute Graphs for Filtered Nearest Neighbor Search

Despite filtered nearest neighbor search being a fundamental task in modern vector search systems, the performance of existing algorithms is highly sensitive to query selectivity and filter type. In particular, existing solutions excel either at specific filter categories (e.g., label equality) or within narrow selectivity bands (e.g., pre-filtering for low selectivity) and are therefore a poor fit for practical deployments that demand generalization to new filter types and unknown query selectivities. In this paper, we propose JAG (Joint Attribute Graphs), a graph-based algorithm designed to deliver robust performance across the entire selectivity spectrum and support diverse filter types. Our key innovation is the introduction of attribute and filter distances, which transform binary filter constraints into continuous navigational guidance. By constructing a proximity graph that jointly optimizes for both vector similarity and attribute proximity, JAG prevents navigational dead-ends and allows JAG to consistently outperform prior graph-based filtered nearest neighbor search methods. Our experimental results across five datasets and four filter types (Label, Range, Subset, Boolean) demonstrate that JAG significantly outperforms existing state-of-the-art baselines in both throughput and recall robustness.

The ParClusterers Benchmark Suite (PCBS): A Fine-Grained Analysis of Scalable Graph Clustering

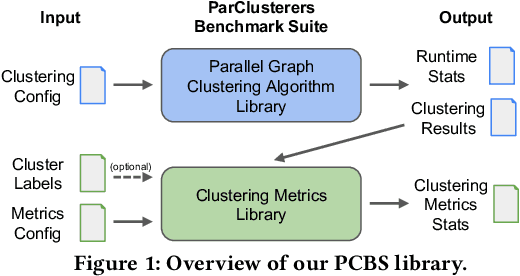
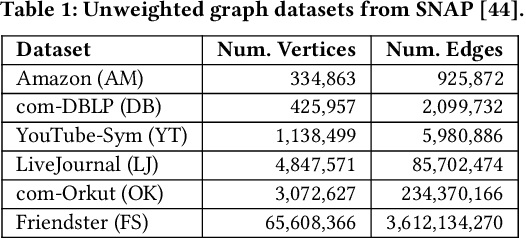
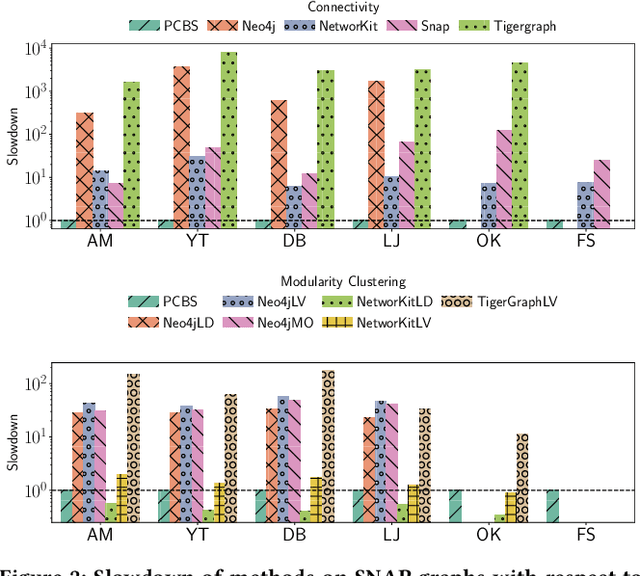
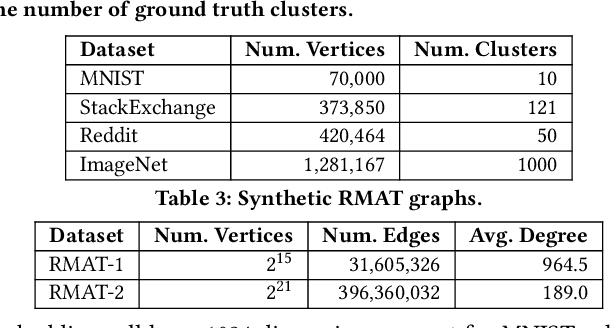
We introduce the ParClusterers Benchmark Suite (PCBS) -- a collection of highly scalable parallel graph clustering algorithms and benchmarking tools that streamline comparing different graph clustering algorithms and implementations. The benchmark includes clustering algorithms that target a wide range of modern clustering use cases, including community detection, classification, and dense subgraph mining. The benchmark toolkit makes it easy to run and evaluate multiple instances of different clustering algorithms, which can be useful for fine-tuning the performance of clustering on a given task, and for comparing different clustering algorithms based on different metrics of interest, including clustering quality and running time. Using PCBS, we evaluate a broad collection of real-world graph clustering datasets. Somewhat surprisingly, we find that the best quality results are obtained by algorithms that not included in many popular graph clustering toolkits. The PCBS provides a standardized way to evaluate and judge the quality-performance tradeoffs of the active research area of scalable graph clustering algorithms. We believe it will help enable fair, accurate, and nuanced evaluation of graph clustering algorithms in the future.

TeraHAC: Hierarchical Agglomerative Clustering of Trillion-Edge Graphs

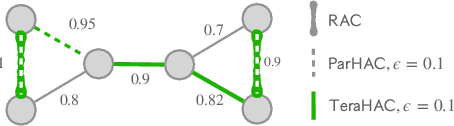
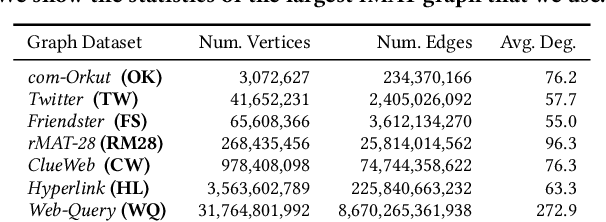
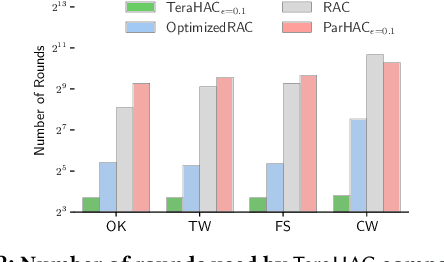
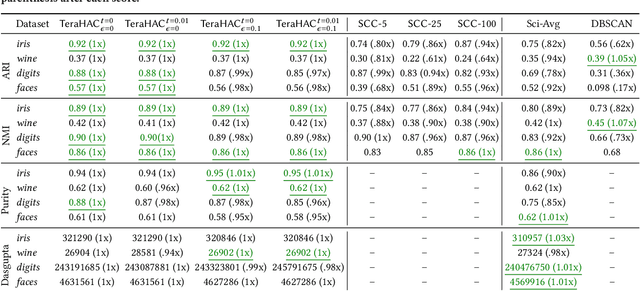
We introduce TeraHAC, a $(1+\epsilon)$-approximate hierarchical agglomerative clustering (HAC) algorithm which scales to trillion-edge graphs. Our algorithm is based on a new approach to computing $(1+\epsilon)$-approximate HAC, which is a novel combination of the nearest-neighbor chain algorithm and the notion of $(1+\epsilon)$-approximate HAC. Our approach allows us to partition the graph among multiple machines and make significant progress in computing the clustering within each partition before any communication with other partitions is needed. We evaluate TeraHAC on a number of real-world and synthetic graphs of up to 8 trillion edges. We show that TeraHAC requires over 100x fewer rounds compared to previously known approaches for computing HAC. It is up to 8.3x faster than SCC, the state-of-the-art distributed algorithm for hierarchical clustering, while achieving 1.16x higher quality. In fact, TeraHAC essentially retains the quality of the celebrated HAC algorithm while significantly improving the running time.

Constant Approximation for Normalized Modularity and Associations Clustering

We study the problem of graph clustering under a broad class of objectives in which the quality of a cluster is defined based on the ratio between the number of edges in the cluster, and the total weight of vertices in the cluster. We show that our definition is closely related to popular clustering measures, namely normalized associations, which is a dual of the normalized cut objective, and normalized modularity. We give a linear time constant-approximate algorithm for our objective, which implies the first constant-factor approximation algorithms for normalized modularity and normalized associations.

Scalable Community Detection via Parallel Correlation Clustering

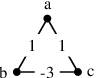
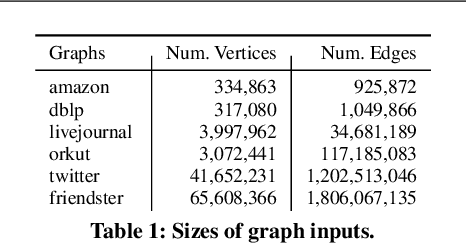
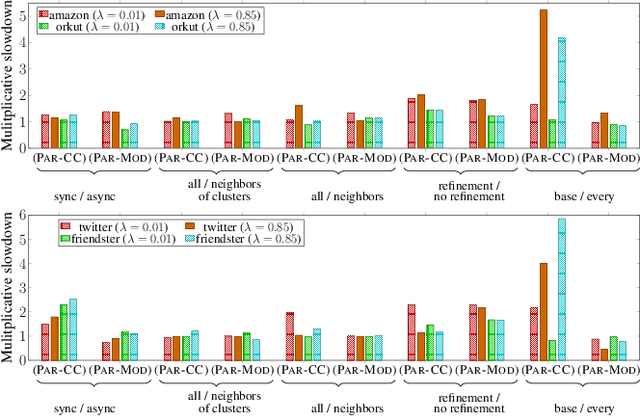
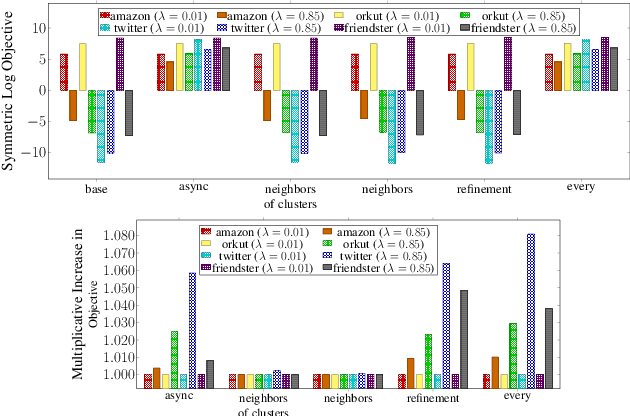
Graph clustering and community detection are central problems in modern data mining. The increasing need for analyzing billion-scale data calls for faster and more scalable algorithms for these problems. There are certain trade-offs between the quality and speed of such clustering algorithms. In this paper, we design scalable algorithms that achieve high quality when evaluated based on ground truth. We develop a generalized sequential and shared-memory parallel framework based on the LambdaCC objective (introduced by Veldt et al.), which encompasses modularity and correlation clustering. Our framework consists of highly-optimized implementations that scale to large data sets of billions of edges and that obtain high-quality clusters compared to ground-truth data, on both unweighted and weighted graphs. Our empirical evaluation shows that this framework improves the state-of-the-art trade-offs between speed and quality of scalable community detection. For example, on a 30-core machine with two-way hyper-threading, our implementations achieve orders of magnitude speedups over other correlation clustering baselines, and up to 28.44x speedups over our own sequential baselines while maintaining or improving quality.

Hierarchical Agglomerative Graph Clustering in Nearly-Linear Time

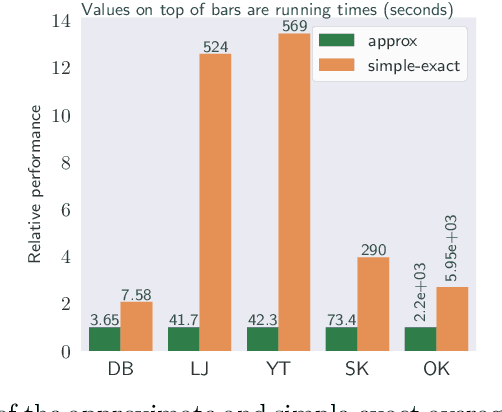
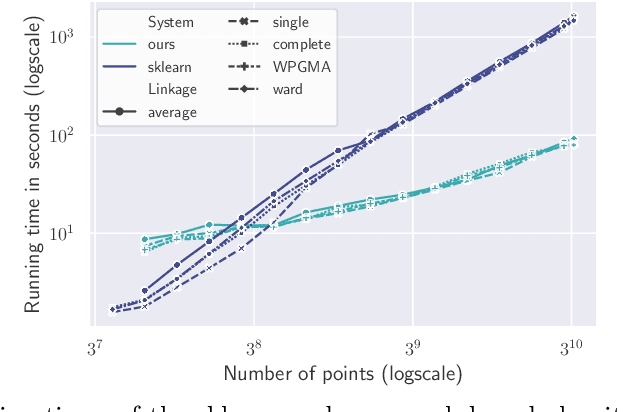
We study the widely used hierarchical agglomerative clustering (HAC) algorithm on edge-weighted graphs. We define an algorithmic framework for hierarchical agglomerative graph clustering that provides the first efficient $\tilde{O}(m)$ time exact algorithms for classic linkage measures, such as complete- and WPGMA-linkage, as well as other measures. Furthermore, for average-linkage, arguably the most popular variant of HAC, we provide an algorithm that runs in $\tilde{O}(n\sqrt{m})$ time. For this variant, this is the first exact algorithm that runs in subquadratic time, as long as $m=n^{2-\epsilon}$ for some constant $\epsilon > 0$. We complement this result with a simple $\epsilon$-close approximation algorithm for average-linkage in our framework that runs in $\tilde{O}(m)$ time. As an application of our algorithms, we consider clustering points in a metric space by first using $k$-NN to generate a graph from the point set, and then running our algorithms on the resulting weighted graph. We validate the performance of our algorithms on publicly available datasets, and show that our approach can speed up clustering of point datasets by a factor of 20.7--76.5x.

Faster DBSCAN via subsampled similarity queries

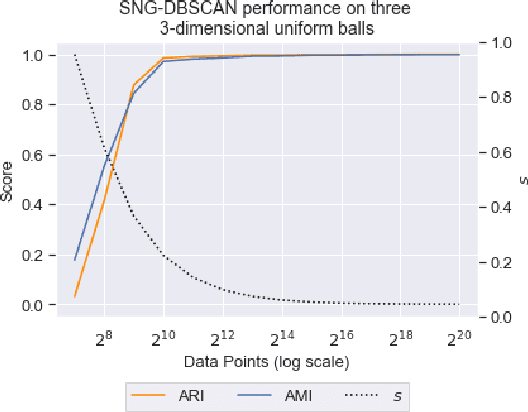
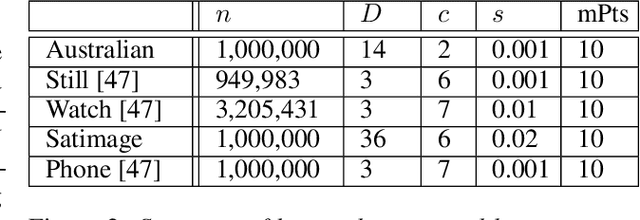
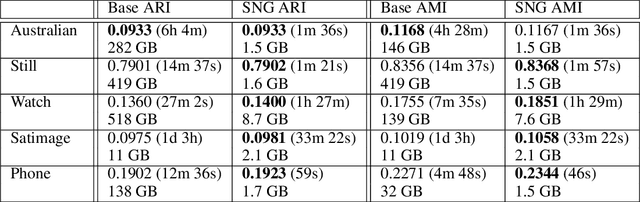
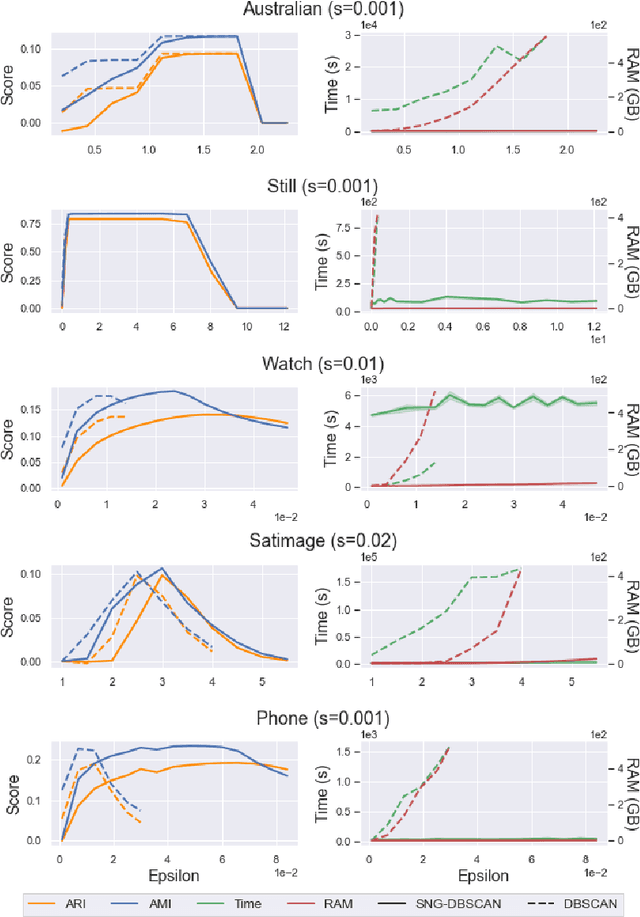
DBSCAN is a popular density-based clustering algorithm. It computes the $\epsilon$-neighborhood graph of a dataset and uses the connected components of the high-degree nodes to decide the clusters. However, the full neighborhood graph may be too costly to compute with a worst-case complexity of $O(n^2)$. In this paper, we propose a simple variant called SNG-DBSCAN, which clusters based on a subsampled $\epsilon$-neighborhood graph, only requires access to similarity queries for pairs of points and in particular avoids any complex data structures which need the embeddings of the data points themselves. The runtime of the procedure is $O(sn^2)$, where $s$ is the sampling rate. We show under some natural theoretical assumptions that $s \approx \log n/n$ is sufficient for statistical cluster recovery guarantees leading to an $O(n\log n)$ complexity. We provide an extensive experimental analysis showing that on large datasets, one can subsample as little as $0.1\%$ of the neighborhood graph, leading to as much as over 200x speedup and 250x reduction in RAM consumption compared to scikit-learn's implementation of DBSCAN, while still maintaining competitive clustering performance.