Jessica Shi
The ParClusterers Benchmark Suite (PCBS): A Fine-Grained Analysis of Scalable Graph Clustering
Nov 15, 2024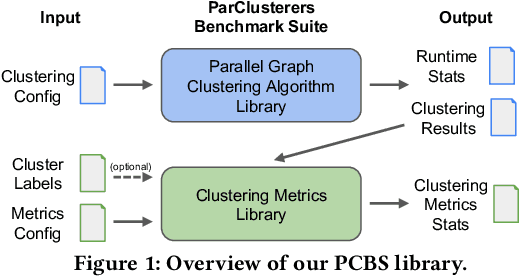
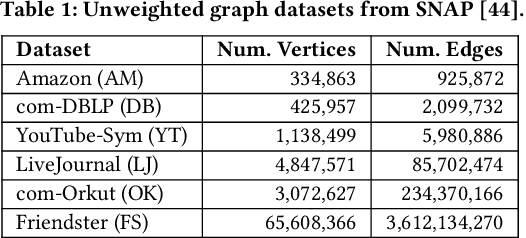
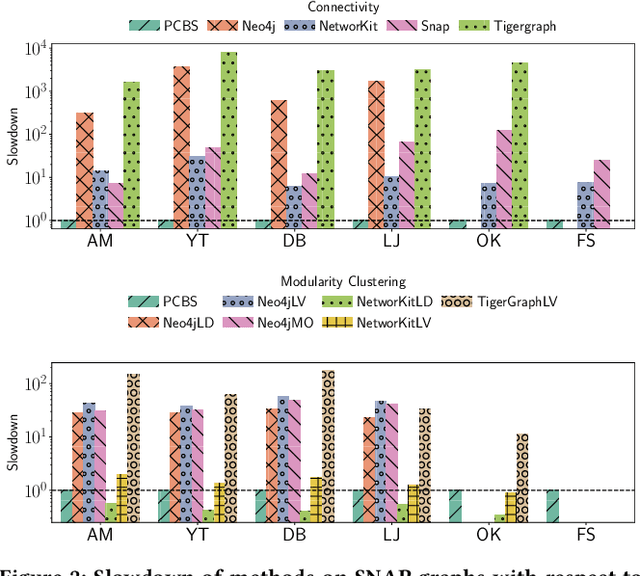
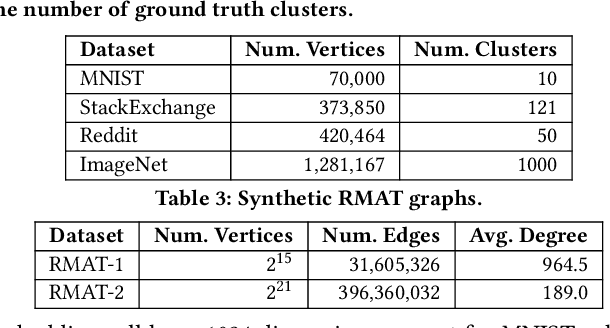
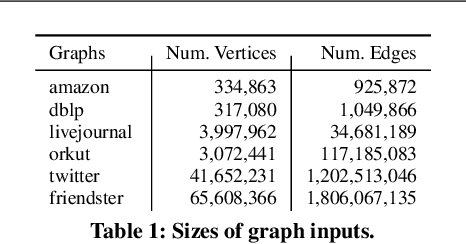
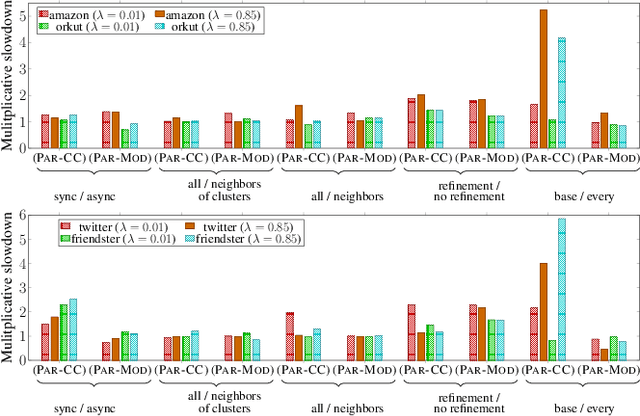
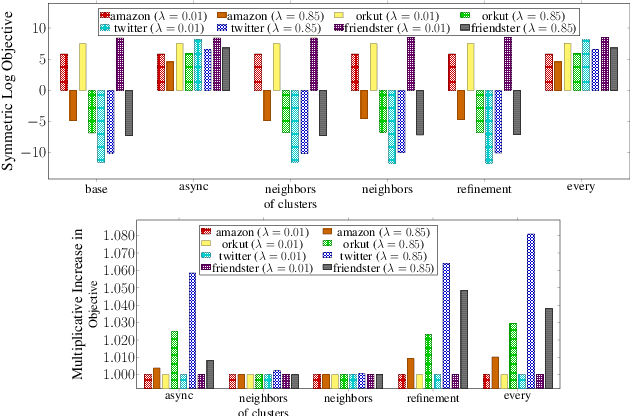
Abstract:We introduce the ParClusterers Benchmark Suite (PCBS) -- a collection of highly scalable parallel graph clustering algorithms and benchmarking tools that streamline comparing different graph clustering algorithms and implementations. The benchmark includes clustering algorithms that target a wide range of modern clustering use cases, including community detection, classification, and dense subgraph mining. The benchmark toolkit makes it easy to run and evaluate multiple instances of different clustering algorithms, which can be useful for fine-tuning the performance of clustering on a given task, and for comparing different clustering algorithms based on different metrics of interest, including clustering quality and running time. Using PCBS, we evaluate a broad collection of real-world graph clustering datasets. Somewhat surprisingly, we find that the best quality results are obtained by algorithms that not included in many popular graph clustering toolkits. The PCBS provides a standardized way to evaluate and judge the quality-performance tradeoffs of the active research area of scalable graph clustering algorithms. We believe it will help enable fair, accurate, and nuanced evaluation of graph clustering algorithms in the future.
Scalable Community Detection via Parallel Correlation Clustering
Jul 27, 2021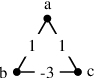
Abstract:Graph clustering and community detection are central problems in modern data mining. The increasing need for analyzing billion-scale data calls for faster and more scalable algorithms for these problems. There are certain trade-offs between the quality and speed of such clustering algorithms. In this paper, we design scalable algorithms that achieve high quality when evaluated based on ground truth. We develop a generalized sequential and shared-memory parallel framework based on the LambdaCC objective (introduced by Veldt et al.), which encompasses modularity and correlation clustering. Our framework consists of highly-optimized implementations that scale to large data sets of billions of edges and that obtain high-quality clusters compared to ground-truth data, on both unweighted and weighted graphs. Our empirical evaluation shows that this framework improves the state-of-the-art trade-offs between speed and quality of scalable community detection. For example, on a 30-core machine with two-way hyper-threading, our implementations achieve orders of magnitude speedups over other correlation clustering baselines, and up to 28.44x speedups over our own sequential baselines while maintaining or improving quality.
Hierarchical Agglomerative Graph Clustering in Nearly-Linear Time
Jun 10, 2021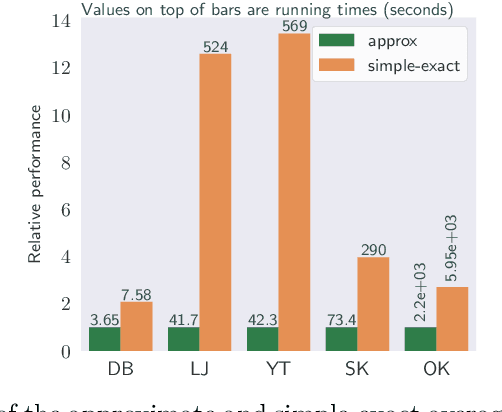

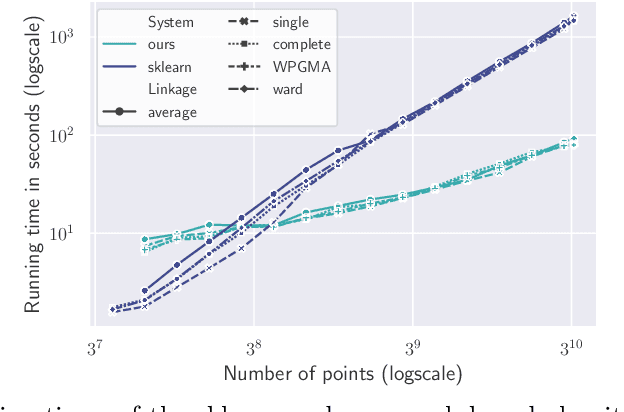
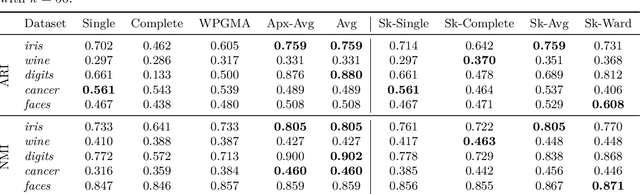
Abstract:We study the widely used hierarchical agglomerative clustering (HAC) algorithm on edge-weighted graphs. We define an algorithmic framework for hierarchical agglomerative graph clustering that provides the first efficient $\tilde{O}(m)$ time exact algorithms for classic linkage measures, such as complete- and WPGMA-linkage, as well as other measures. Furthermore, for average-linkage, arguably the most popular variant of HAC, we provide an algorithm that runs in $\tilde{O}(n\sqrt{m})$ time. For this variant, this is the first exact algorithm that runs in subquadratic time, as long as $m=n^{2-\epsilon}$ for some constant $\epsilon > 0$. We complement this result with a simple $\epsilon$-close approximation algorithm for average-linkage in our framework that runs in $\tilde{O}(m)$ time. As an application of our algorithms, we consider clustering points in a metric space by first using $k$-NN to generate a graph from the point set, and then running our algorithms on the resulting weighted graph. We validate the performance of our algorithms on publicly available datasets, and show that our approach can speed up clustering of point datasets by a factor of 20.7--76.5x.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge