MeanShift++: Extremely Fast Mode-Seeking With Applications to Segmentation and Object Tracking

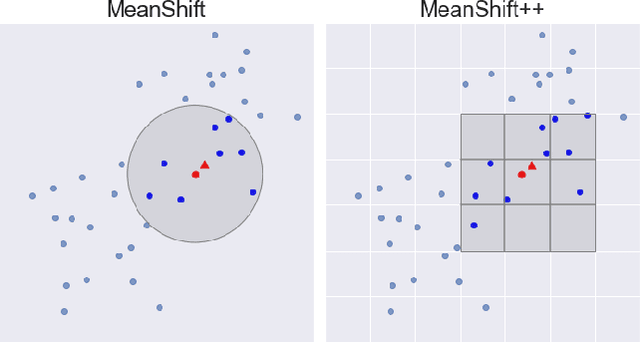
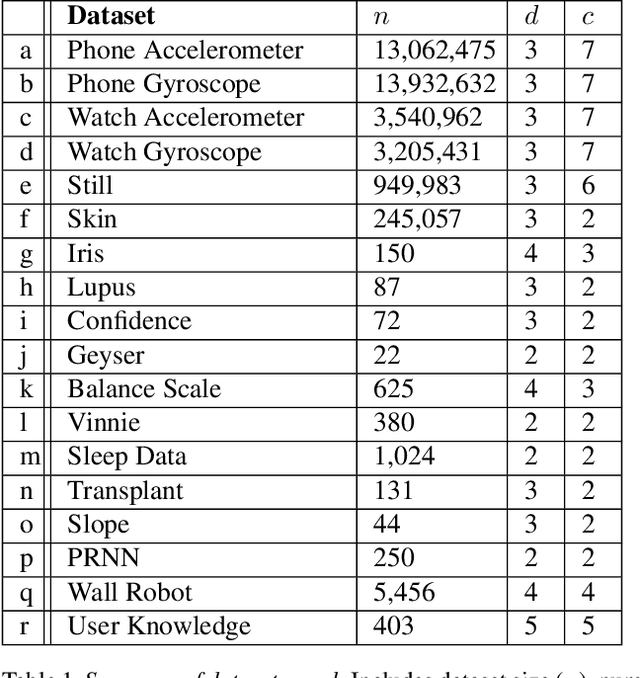
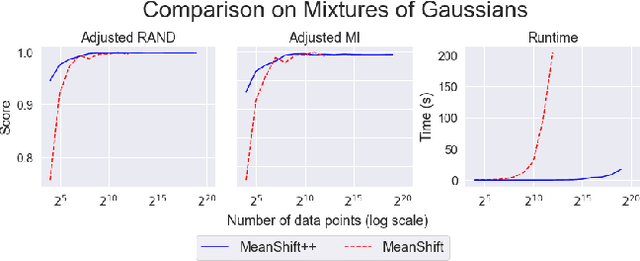
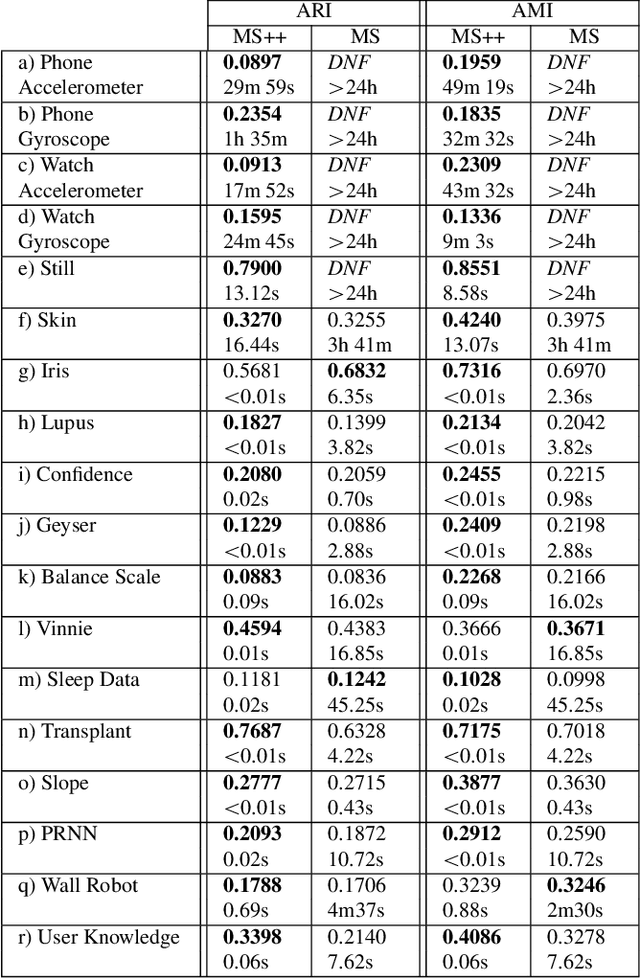
MeanShift is a popular mode-seeking clustering algorithm used in a wide range of applications in machine learning. However, it is known to be prohibitively slow, with quadratic runtime per iteration. We propose MeanShift++, an extremely fast mode-seeking algorithm based on MeanShift that uses a grid-based approach to speed up the mean shift step, replacing the computationally expensive neighbors search with a density-weighted mean of adjacent grid cells. In addition, we show that this grid-based technique for density estimation comes with theoretical guarantees. The runtime is linear in the number of points and exponential in dimension, which makes MeanShift++ ideal on low-dimensional applications such as image segmentation and object tracking. We provide extensive experimental analysis showing that MeanShift++ can be more than 10,000x faster than MeanShift with competitive clustering results on benchmark datasets and nearly identical image segmentations as MeanShift. Finally, we show promising results for object tracking.

Faster DBSCAN via subsampled similarity queries

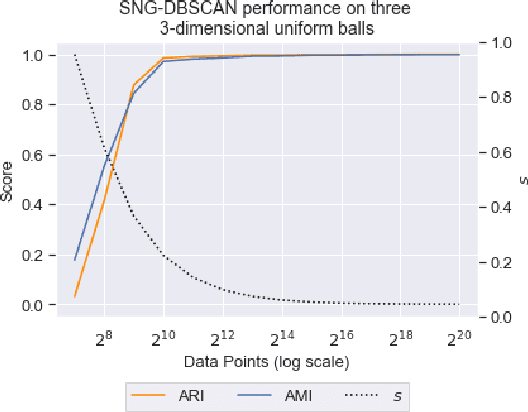
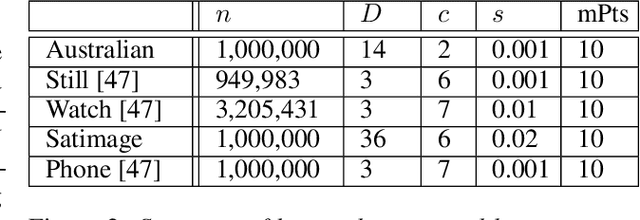
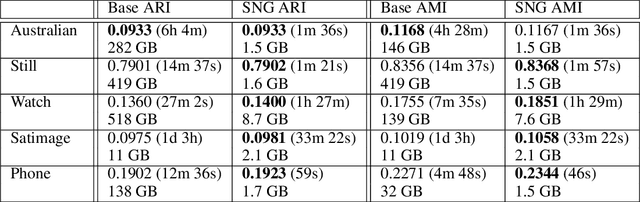
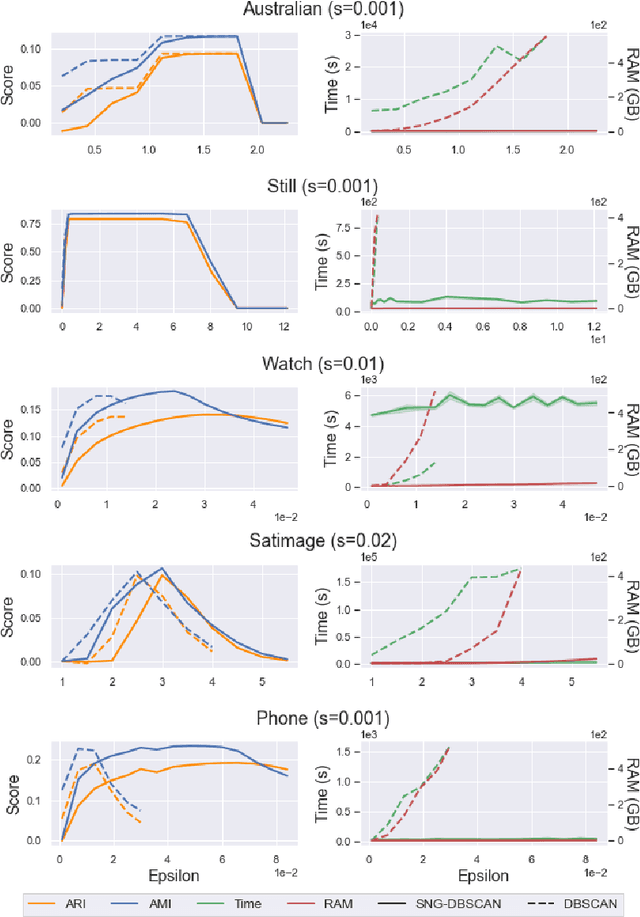
DBSCAN is a popular density-based clustering algorithm. It computes the $\epsilon$-neighborhood graph of a dataset and uses the connected components of the high-degree nodes to decide the clusters. However, the full neighborhood graph may be too costly to compute with a worst-case complexity of $O(n^2)$. In this paper, we propose a simple variant called SNG-DBSCAN, which clusters based on a subsampled $\epsilon$-neighborhood graph, only requires access to similarity queries for pairs of points and in particular avoids any complex data structures which need the embeddings of the data points themselves. The runtime of the procedure is $O(sn^2)$, where $s$ is the sampling rate. We show under some natural theoretical assumptions that $s \approx \log n/n$ is sufficient for statistical cluster recovery guarantees leading to an $O(n\log n)$ complexity. We provide an extensive experimental analysis showing that on large datasets, one can subsample as little as $0.1\%$ of the neighborhood graph, leading to as much as over 200x speedup and 250x reduction in RAM consumption compared to scikit-learn's implementation of DBSCAN, while still maintaining competitive clustering performance.

DBSCAN++: Towards fast and scalable density clustering

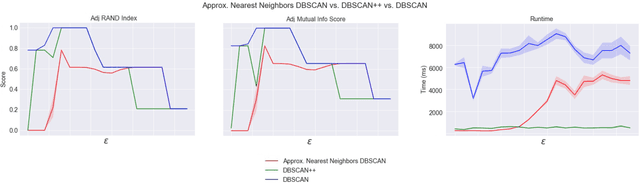
DBSCAN is a classical density-based clustering procedure which has had tremendous practical relevance. However, it implicitly needs to compute the empirical density for each sample point, leading to a quadratic worst-case time complexity, which may be too slow on large datasets. We propose DBSCAN++, a simple modification of DBSCAN which only requires computing the densities for a subset of the points. We show empirically that, compared to traditional DBSCAN, DBSCAN++ can provide not only competitive performance but also added robustness in the bandwidth hyperparameter while taking a fraction of the runtime. We also present statistical consistency guarantees showing the trade-off between computational cost and estimation rates. Surprisingly, up to a certain point, we can enjoy the same estimation rates while lowering computational cost, showing that DBSCAN++ is a sub-quadratic algorithm that attains minimax optimal rates for level-set estimation, a quality that may be of independent interest.

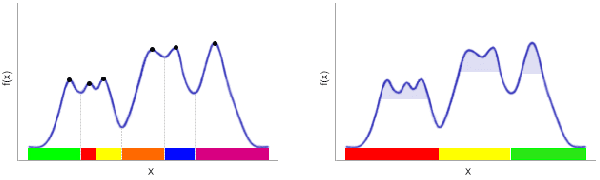
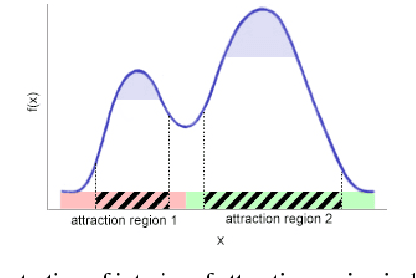
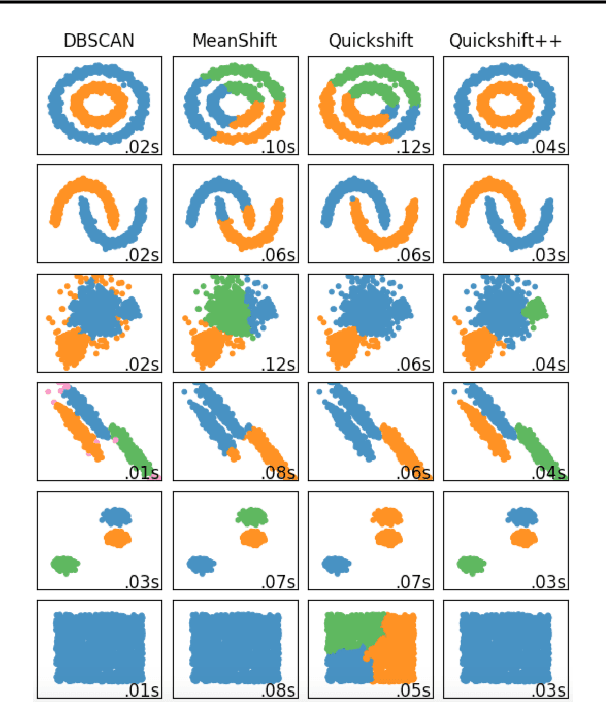
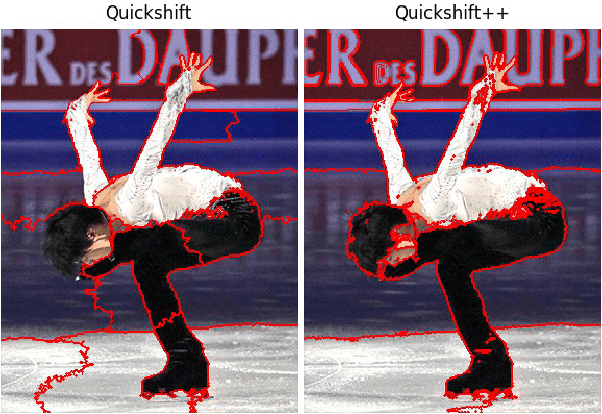
Quickshift++: Provably Good Initializations for Sample-Based Mean Shift

We provide initial seedings to the Quick Shift clustering algorithm, which approximate the locally high-density regions of the data. Such seedings act as more stable and expressive cluster-cores than the singleton modes found by Quick Shift. We establish statistical consistency guarantees for this modification. We then show strong clustering performance on real datasets as well as promising applications to image segmentation.