DBSCAN++: Towards fast and scalable density clustering

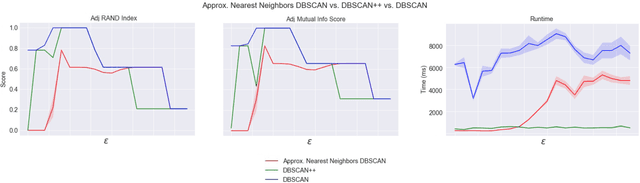
DBSCAN is a classical density-based clustering procedure which has had tremendous practical relevance. However, it implicitly needs to compute the empirical density for each sample point, leading to a quadratic worst-case time complexity, which may be too slow on large datasets. We propose DBSCAN++, a simple modification of DBSCAN which only requires computing the densities for a subset of the points. We show empirically that, compared to traditional DBSCAN, DBSCAN++ can provide not only competitive performance but also added robustness in the bandwidth hyperparameter while taking a fraction of the runtime. We also present statistical consistency guarantees showing the trade-off between computational cost and estimation rates. Surprisingly, up to a certain point, we can enjoy the same estimation rates while lowering computational cost, showing that DBSCAN++ is a sub-quadratic algorithm that attains minimax optimal rates for level-set estimation, a quality that may be of independent interest.