Fast Parallel Algorithms for Euclidean Minimum Spanning Tree and Hierarchical Spatial Clustering
Paper and Code
Apr 02, 2021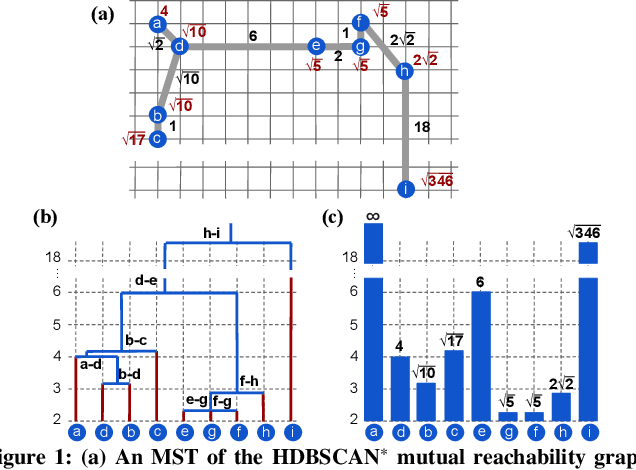

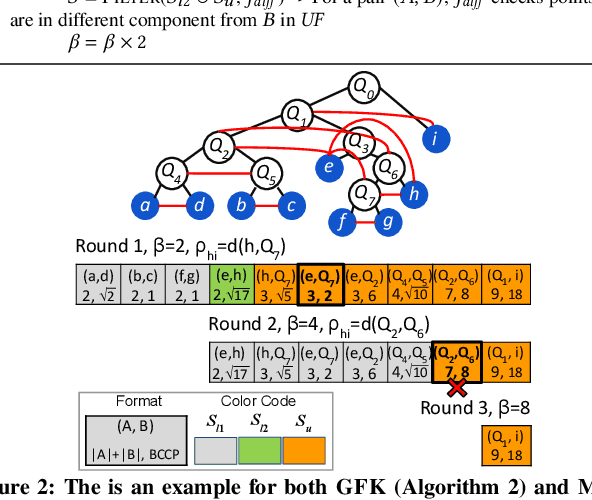
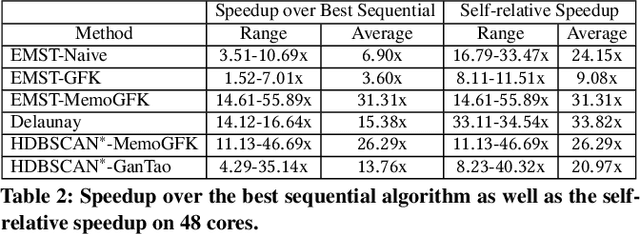
This paper presents new parallel algorithms for generating Euclidean minimum spanning trees and spatial clustering hierarchies (known as HDBSCAN$^*$). Our approach is based on generating a well-separated pair decomposition followed by using Kruskal's minimum spanning tree algorithm and bichromatic closest pair computations. We introduce a new notion of well-separation to reduce the work and space of our algorithm for HDBSCAN$^*$. We also present a parallel approximate algorithm for OPTICS based on a recent sequential algorithm by Gan and Tao. Finally, we give a new parallel divide-and-conquer algorithm for computing the dendrogram and reachability plots, which are used in visualizing clusters of different scale that arise for both EMST and HDBSCAN$^*$. We show that our algorithms are theoretically efficient: they have work (number of operations) matching their sequential counterparts, and polylogarithmic depth (parallel time). We implement our algorithms and propose a memory optimization that requires only a subset of well-separated pairs to be computed and materialized, leading to savings in both space (up to 10x) and time (up to 8x). Our experiments on large real-world and synthetic data sets using a 48-core machine show that our fastest algorithms outperform the best serial algorithms for the problems by 11.13--55.89x, and existing parallel algorithms by at least an order of magnitude.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge