GeoPT: Scaling Physics Simulation via Lifted Geometric Pre-Training

Neural simulators promise efficient surrogates for physics simulation, but scaling them is bottlenecked by the prohibitive cost of generating high-fidelity training data. Pre-training on abundant off-the-shelf geometries offers a natural alternative, yet faces a fundamental gap: supervision on static geometry alone ignores dynamics and can lead to negative transfer on physics tasks. We present GeoPT, a unified pre-trained model for general physics simulation based on lifted geometric pre-training. The core idea is to augment geometry with synthetic dynamics, enabling dynamics-aware self-supervision without physics labels. Pre-trained on over one million samples, GeoPT consistently improves industrial-fidelity benchmarks spanning fluid mechanics for cars, aircraft, and ships, and solid mechanics in crash simulation, reducing labeled data requirements by 20-60% and accelerating convergence by 2$\times$. These results show that lifting with synthetic dynamics bridges the geometry-physics gap, unlocking a scalable path for neural simulation and potentially beyond. Code is available at https://github.com/Physics-Scaling/GeoPT.

Latent Generative Solvers for Generalizable Long-Term Physics Simulation

We study long-horizon surrogate simulation across heterogeneous PDE systems. We introduce Latent Generative Solvers (LGS), a two-stage framework that (i) maps diverse PDE states into a shared latent physics space with a pretrained VAE, and (ii) learns probabilistic latent dynamics with a Transformer trained by flow matching. Our key mechanism is an uncertainty knob that perturbs latent inputs during training and inference, teaching the solver to correct off-manifold rollout drift and stabilizing autoregressive prediction. We further use flow forcing to update a system descriptor (context) from model-generated trajectories, aligning train/test conditioning and improving long-term stability. We pretrain on a curated corpus of $\sim$2.5M trajectories at $128^2$ resolution spanning 12 PDE families. LGS matches strong deterministic neural-operator baselines on short horizons while substantially reducing rollout drift on long horizons. Learning in latent space plus efficient architectural choices yields up to \textbf{70$\times$} lower FLOPs than non-generative baselines, enabling scalable pretraining. We also show efficient adaptation to an out-of-distribution $256^2$ Kolmogorov flow dataset under limited finetuning budgets. Overall, LGS provides a practical route toward generalizable, uncertainty-aware neural PDE solvers that are more reliable for long-term forecasting and downstream scientific workflows.

Brep2Shape: Boundary and Shape Representation Alignment via Self-Supervised Transformers

Boundary representation (B-rep) is the industry standard for computer-aided design (CAD). While deep learning shows promise in processing B-rep models, existing methods suffer from a representation gap: continuous approaches offer analytical precision but are visually abstract, whereas discrete methods provide intuitive clarity at the expense of geometric precision. To bridge this gap, we introduce Brep2Shape, a novel self-supervised pre-training method designed to align abstract boundary representations with intuitive shape representations. Our method employs a geometry-aware task where the model learns to predict dense spatial points from parametric Bézier control points, enabling the network to better understand physical manifolds derived from abstract coefficients. To enhance this alignment, we propose a Dual Transformer backbone with parallel streams that independently encode surface and curve tokens to capture their distinct geometric properties. Moreover, the topology attention is integrated to model the interdependencies between surfaces and curves, thereby maintaining topological consistency. Experimental results demonstrate that Brep2Shape offers significant scalability, achieving state-of-the-art accuracy and faster convergence across various downstream tasks.

Transolver-3: Scaling Up Transformer Solvers to Industrial-Scale Geometries

Deep learning has emerged as a transformative tool for the neural surrogate modeling of partial differential equations (PDEs), known as neural PDE solvers. However, scaling these solvers to industrial-scale geometries with over $10^8$ cells remains a fundamental challenge due to the prohibitive memory complexity of processing high-resolution meshes. We present Transolver-3, a new member of the Transolver family as a highly scalable framework designed for high-fidelity physics simulations. To bridge the gap between limited GPU capacity and the resolution requirements of complex engineering tasks, we introduce two key architectural optimizations: faster slice and deslice by exploiting matrix multiplication associative property and geometry slice tiling to partition the computation of physical states. Combined with an amortized training strategy by learning on random subsets of original high-resolution meshes and a physical state caching technique during inference, Transolver-3 enables high-fidelity field prediction on industrial-scale meshes. Extensive experiments demonstrate that Transolver-3 is capable of handling meshes with over 160 million cells, achieving impressive performance across three challenging simulation benchmarks, including aircraft and automotive design tasks.

Neural Modular Physics for Elastic Simulation

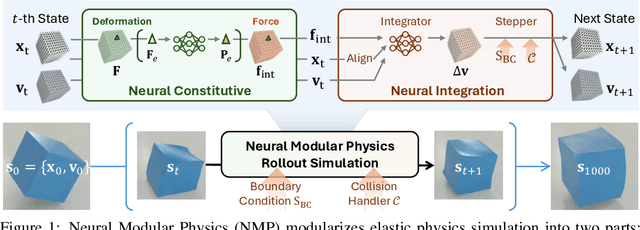
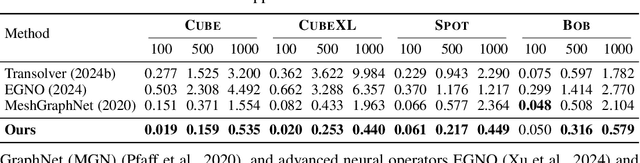
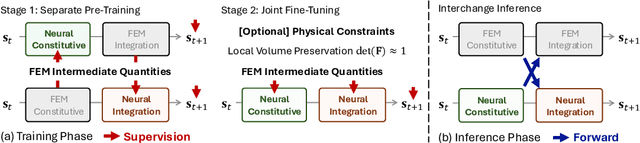
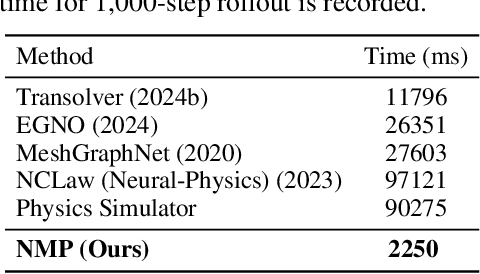
Learning-based methods have made significant progress in physics simulation, typically approximating dynamics with a monolithic end-to-end optimized neural network. Although these models offer an effective way to simulation, they may lose essential features compared to traditional numerical simulators, such as physical interpretability and reliability. Drawing inspiration from classical simulators that operate in a modular fashion, this paper presents Neural Modular Physics (NMP) for elastic simulation, which combines the approximation capacity of neural networks with the physical reliability of traditional simulators. Beyond the previous monolithic learning paradigm, NMP enables direct supervision of intermediate quantities and physical constraints by decomposing elastic dynamics into physically meaningful neural modules connected through intermediate physical quantities. With a specialized architecture and training strategy, our method transforms the numerical computation flow into a modular neural simulator, achieving improved physical consistency and generalizability. Experimentally, NMP demonstrates superior generalization to unseen initial conditions and resolutions, stable long-horizon simulation, better preservation of physical properties compared to other neural simulators, and greater feasibility in scenarios with unknown underlying dynamics than traditional simulators.

FlashBias: Fast Computation of Attention with Bias

Attention mechanism has emerged as a foundation module of modern deep learning models and has also empowered many milestones in various domains. Moreover, FlashAttention with IO-aware speedup resolves the efficiency issue of standard attention, further promoting its practicality. Beyond canonical attention, attention with bias also widely exists, such as relative position bias in vision and language models and pair representation bias in AlphaFold. In these works, prior knowledge is introduced as an additive bias term of attention weights to guide the learning process, which has been proven essential for model performance. Surprisingly, despite the common usage of attention with bias, its targeted efficiency optimization is still absent, which seriously hinders its wide applications in complex tasks. Diving into the computation of FlashAttention, we prove that its optimal efficiency is determined by the rank of the attention weight matrix. Inspired by this theoretical result, this paper presents FlashBias based on the low-rank compressed sensing theory, which can provide fast-exact computation for many widely used attention biases and a fast-accurate approximation for biases in general formalization. FlashBias can fully take advantage of the extremely optimized matrix multiplication operation in modern GPUs, achieving 1.5$\times$ speedup for AlphaFold, and over 2$\times$ speedup for attention with bias in vision and language models without loss of accuracy.

Transolver++: An Accurate Neural Solver for PDEs on Million-Scale Geometries

Although deep models have been widely explored in solving partial differential equations (PDEs), previous works are primarily limited to data only with up to tens of thousands of mesh points, far from the million-point scale required by industrial simulations that involve complex geometries. In the spirit of advancing neural PDE solvers to real industrial applications, we present Transolver++, a highly parallel and efficient neural solver that can accurately solve PDEs on million-scale geometries. Building upon previous advancements in solving PDEs by learning physical states via Transolver, Transolver++ is further equipped with an extremely optimized parallelism framework and a local adaptive mechanism to efficiently capture eidetic physical states from massive mesh points, successfully tackling the thorny challenges in computation and physics learning when scaling up input mesh size. Transolver++ increases the single-GPU input capacity to million-scale points for the first time and is capable of continuously scaling input size in linear complexity by increasing GPUs. Experimentally, Transolver++ yields 13% relative promotion across six standard PDE benchmarks and achieves over 20% performance gain in million-scale high-fidelity industrial simulations, whose sizes are 100$\times$ larger than previous benchmarks, covering car and 3D aircraft designs.

ProPINN: Demystifying Propagation Failures in Physics-Informed Neural Networks

Physics-informed neural networks (PINNs) have earned high expectations in solving partial differential equations (PDEs), but their optimization usually faces thorny challenges due to the unique derivative-dependent loss function. By analyzing the loss distribution, previous research observed the propagation failure phenomenon of PINNs, intuitively described as the correct supervision for model outputs cannot ``propagate'' from initial states or boundaries to the interior domain. Going beyond intuitive understanding, this paper provides the first formal and in-depth study of propagation failure and its root cause. Based on a detailed comparison with classical finite element methods, we ascribe the failure to the conventional single-point-processing architecture of PINNs and further prove that propagation failure is essentially caused by the lower gradient correlation of PINN models on nearby collocation points. Compared to superficial loss maps, this new perspective provides a more precise quantitative criterion to identify where and why PINN fails. The theoretical finding also inspires us to present a new PINN architecture, named ProPINN, which can effectively unite the gradient of region points for better propagation. ProPINN can reliably resolve PINN failure modes and significantly surpass advanced Transformer-based models with 46% relative promotion.

Metadata Matters for Time Series: Informative Forecasting with Transformers

Time series forecasting is prevalent in extensive real-world applications, such as financial analysis and energy planning. Previous studies primarily focus on time series modality, endeavoring to capture the intricate variations and dependencies inherent in time series. Beyond numerical time series data, we notice that metadata (e.g.~dataset and variate descriptions) also carries valuable information essential for forecasting, which can be used to identify the application scenario and provide more interpretable knowledge than digit sequences. Inspired by this observation, we propose a Metadata-informed Time Series Transformer (MetaTST), which incorporates multiple levels of context-specific metadata into Transformer forecasting models to enable informative time series forecasting. To tackle the unstructured nature of metadata, MetaTST formalizes them into natural languages by pre-designed templates and leverages large language models (LLMs) to encode these texts into metadata tokens as a supplement to classic series tokens, resulting in an informative embedding. Further, a Transformer encoder is employed to communicate series and metadata tokens, which can extend series representations by metadata information for more accurate forecasting. This design also allows the model to adaptively learn context-specific patterns across various scenarios, which is particularly effective in handling large-scale, diverse-scenario forecasting tasks. Experimentally, MetaTST achieves state-of-the-art compared to advanced time series models and LLM-based methods on widely acknowledged short- and long-term forecasting benchmarks, covering both single-dataset individual and multi-dataset joint training settings.

Deep Time Series Models: A Comprehensive Survey and Benchmark

Time series, characterized by a sequence of data points arranged in a discrete-time order, are ubiquitous in real-world applications. Different from other modalities, time series present unique challenges due to their complex and dynamic nature, including the entanglement of nonlinear patterns and time-variant trends. Analyzing time series data is of great significance in real-world scenarios and has been widely studied over centuries. Recent years have witnessed remarkable breakthroughs in the time series community, with techniques shifting from traditional statistical methods to advanced deep learning models. In this paper, we delve into the design of deep time series models across various analysis tasks and review the existing literature from two perspectives: basic modules and model architectures. Further, we develop and release Time Series Library (TSLib) as a fair benchmark of deep time series models for diverse analysis tasks, which implements 24 mainstream models, covers 30 datasets from different domains, and supports five prevalent analysis tasks. Based on TSLib, we thoroughly evaluate 12 advanced deep time series models on different tasks. Empirical results indicate that models with specific structures are well-suited for distinct analytical tasks, which offers insights for research and adoption of deep time series models. Code is available at https://github.com/thuml/Time-Series-Library.