EuLagNet: Eulerian Fluid Prediction with Lagrangian Dynamics

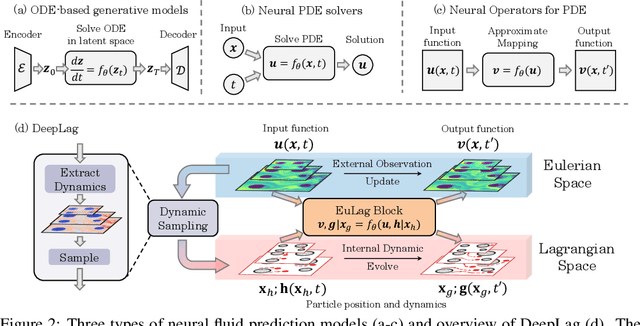
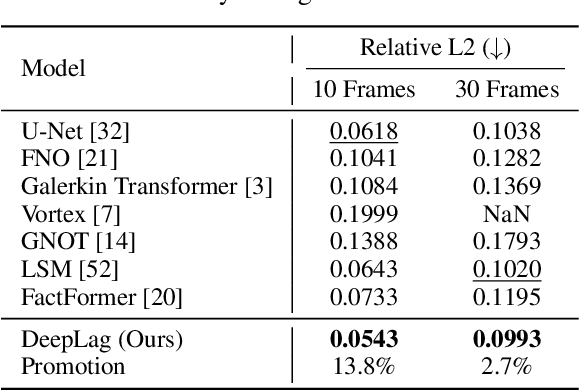
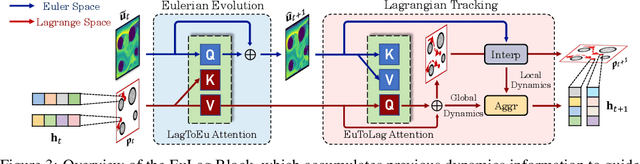
Accurately predicting the future fluid is important to extensive areas, such as meteorology, oceanology and aerodynamics. However, since the fluid is usually observed from an Eulerian perspective, its active and intricate dynamics are seriously obscured and confounded in static grids, bringing horny challenges to the prediction. This paper introduces a new Lagrangian-guided paradigm to tackle the tanglesome fluid dynamics. Instead of solely predicting the future based on Eulerian observations, we propose the Eulerian-Lagrangian Dual Recurrent Network (EuLagNet), which captures multiscale fluid dynamics by tracking movements of adaptively sampled key particles on multiple scales and integrating dynamics information over time. Concretely, a EuLag Block is presented to communicate the learned Eulerian and Lagrangian features at each moment and scale, where the motion of tracked particles is inferred from Eulerian observations and their accumulated dynamics information is incorporated into Eulerian fields to guide future prediction. Tracking key particles not only provides a clear and interpretable clue for fluid dynamics but also makes our model free from modeling complex correlations among massive grids for better efficiency. Experimentally, EuLagNet excels in three challenging fluid prediction tasks, covering both 2D and 3D, simulated and real-world fluids.

HelmSim: Learning Helmholtz Dynamics for Interpretable Fluid Simulation

Fluid simulation is a long-standing challenge due to the intrinsic high-dimensional non-linear dynamics. Previous methods usually utilize the non-linear modeling capability of deep models to directly estimate velocity fields for future prediction. However, skipping over inherent physical properties but directly learning superficial velocity fields will overwhelm the model from generating precise or physics-reliable results. In this paper, we propose the HelmSim toward an accurate and interpretable simulator for fluid. Inspired by the Helmholtz theorem, we design a HelmDynamic block to learn the Helmholtz dynamics, which decomposes fluid dynamics into more solvable curl-free and divergence-free parts, physically corresponding to potential and stream functions of fluid. By embedding the HelmDynamic block into a Multiscale Integration Network, HelmSim can integrate learned Helmholtz dynamics along temporal dimension in multiple spatial scales to yield future fluid. Comparing with previous velocity estimating methods, HelmSim is faithfully derived from Helmholtz theorem and ravels out complex fluid dynamics with physically interpretable evidence. Experimentally, our proposed HelmSim achieves the consistent state-of-the-art in both numerical simulated and real-world observed benchmarks, even for scenarios with complex boundaries.