Feiping Nie
The University of Texas at Arlington
FusAD: Time-Frequency Fusion with Adaptive Denoising for General Time Series Analysis
Dec 16, 2025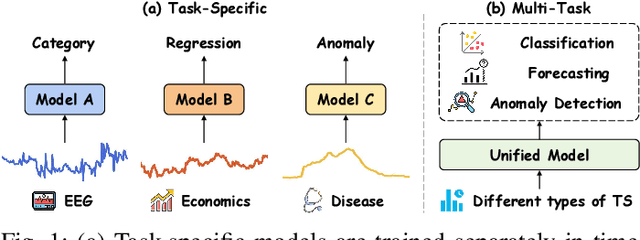
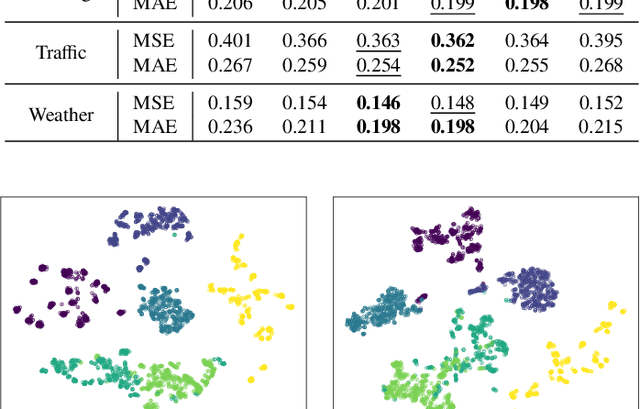


Abstract:Time series analysis plays a vital role in fields such as finance, healthcare, industry, and meteorology, underpinning key tasks including classification, forecasting, and anomaly detection. Although deep learning models have achieved remarkable progress in these areas in recent years, constructing an efficient, multi-task compatible, and generalizable unified framework for time series analysis remains a significant challenge. Existing approaches are often tailored to single tasks or specific data types, making it difficult to simultaneously handle multi-task modeling and effectively integrate information across diverse time series types. Moreover, real-world data are often affected by noise, complex frequency components, and multi-scale dynamic patterns, which further complicate robust feature extraction and analysis. To ameliorate these challenges, we propose FusAD, a unified analysis framework designed for diverse time series tasks. FusAD features an adaptive time-frequency fusion mechanism, integrating both Fourier and Wavelet transforms to efficiently capture global-local and multi-scale dynamic features. With an adaptive denoising mechanism, FusAD automatically senses and filters various types of noise, highlighting crucial sequence variations and enabling robust feature extraction in complex environments. In addition, the framework integrates a general information fusion and decoding structure, combined with masked pre-training, to promote efficient learning and transfer of multi-granularity representations. Extensive experiments demonstrate that FusAD consistently outperforms state-of-the-art models on mainstream time series benchmarks for classification, forecasting, and anomaly detection tasks, while maintaining high efficiency and scalability. Code is available at https://github.com/zhangda1018/FusAD.
Towards Federated Clustering: A Client-wise Private Graph Aggregation Framework
Nov 14, 2025



Abstract:Federated clustering addresses the critical challenge of extracting patterns from decentralized, unlabeled data. However, it is hampered by the flaw that current approaches are forced to accept a compromise between performance and privacy: \textit{transmitting embedding representations risks sensitive data leakage, while sharing only abstract cluster prototypes leads to diminished model accuracy}. To resolve this dilemma, we propose Structural Privacy-Preserving Federated Graph Clustering (SPP-FGC), a novel algorithm that innovatively leverages local structural graphs as the primary medium for privacy-preserving knowledge sharing, thus moving beyond the limitations of conventional techniques. Our framework operates on a clear client-server logic; on the client-side, each participant constructs a private structural graph that captures intrinsic data relationships, which the server then securely aggregates and aligns to form a comprehensive global graph from which a unified clustering structure is derived. The framework offers two distinct modes to suit different needs. SPP-FGC is designed as an efficient one-shot method that completes its task in a single communication round, ideal for rapid analysis. For more complex, unstructured data like images, SPP-FGC+ employs an iterative process where clients and the server collaboratively refine feature representations to achieve superior downstream performance. Extensive experiments demonstrate that our framework achieves state-of-the-art performance, improving clustering accuracy by up to 10\% (NMI) over federated baselines while maintaining provable privacy guarantees.
Dynamic Manipulation of Deformable Objects in 3D: Simulation, Benchmark and Learning Strategy
May 23, 2025Abstract:Goal-conditioned dynamic manipulation is inherently challenging due to complex system dynamics and stringent task constraints, particularly in deformable object scenarios characterized by high degrees of freedom and underactuation. Prior methods often simplify the problem to low-speed or 2D settings, limiting their applicability to real-world 3D tasks. In this work, we explore 3D goal-conditioned rope manipulation as a representative challenge. To mitigate data scarcity, we introduce a novel simulation framework and benchmark grounded in reduced-order dynamics, which enables compact state representation and facilitates efficient policy learning. Building on this, we propose Dynamics Informed Diffusion Policy (DIDP), a framework that integrates imitation pretraining with physics-informed test-time adaptation. First, we design a diffusion policy that learns inverse dynamics within the reduced-order space, enabling imitation learning to move beyond na\"ive data fitting and capture the underlying physical structure. Second, we propose a physics-informed test-time adaptation scheme that imposes kinematic boundary conditions and structured dynamics priors on the diffusion process, ensuring consistency and reliability in manipulation execution. Extensive experiments validate the proposed approach, demonstrating strong performance in terms of accuracy and robustness in the learned policy.
Riemannian Optimization on Relaxed Indicator Matrix Manifold
Mar 26, 2025Abstract:The indicator matrix plays an important role in machine learning, but optimizing it is an NP-hard problem. We propose a new relaxation of the indicator matrix and prove that this relaxation forms a manifold, which we call the Relaxed Indicator Matrix Manifold (RIM manifold). Based on Riemannian geometry, we develop a Riemannian toolbox for optimization on the RIM manifold. Specifically, we provide several methods of Retraction, including a fast Retraction method to obtain geodesics. We point out that the RIM manifold is a generalization of the double stochastic manifold, and it is much faster than existing methods on the double stochastic manifold, which has a complexity of \( \mathcal{O}(n^3) \), while RIM manifold optimization is \( \mathcal{O}(n) \) and often yields better results. We conducted extensive experiments, including image denoising, with millions of variables to support our conclusion, and applied the RIM manifold to Ratio Cut, achieving clustering results that outperform the state-of-the-art methods. Our Code in \href{https://github.com/Yuan-Jinghui/Riemannian-Optimization-on-Relaxed-Indicator-Matrix-Manifold}{https://github.com/Yuan-Jinghui/Riemannian-Optimization-on-Relaxed-Indicator-Matrix-Manifold}.
Dual-Bounded Nonlinear Optimal Transport for Size Constrained Min Cut Clustering
Jan 30, 2025



Abstract:Min cut is an important graph partitioning method. However, current solutions to the min cut problem suffer from slow speeds, difficulty in solving, and often converge to simple solutions. To address these issues, we relax the min cut problem into a dual-bounded constraint and, for the first time, treat the min cut problem as a dual-bounded nonlinear optimal transport problem. Additionally, we develop a method for solving dual-bounded nonlinear optimal transport based on the Frank-Wolfe method (abbreviated as DNF). Notably, DNF not only solves the size constrained min cut problem but is also applicable to all dual-bounded nonlinear optimal transport problems. We prove that for convex problems satisfying Lipschitz smoothness, the DNF method can achieve a convergence rate of \(\mathcal{O}(\frac{1}{t})\). We apply the DNF method to the min cut problem and find that it achieves state-of-the-art performance in terms of both the loss function and clustering accuracy at the fastest speed, with a convergence rate of \(\mathcal{O}(\frac{1}{\sqrt{t}})\). Moreover, the DNF method for the size constrained min cut problem requires no parameters and exhibits better stability.
A Greedy Strategy for Graph Cut
Dec 28, 2024



Abstract:We propose a Greedy strategy to solve the problem of Graph Cut, called GGC. It starts from the state where each data sample is regarded as a cluster and dynamically merges the two clusters which reduces the value of the global objective function the most until the required number of clusters is obtained, and the monotonicity of the sequence of objective function values is proved. To reduce the computational complexity of GGC, only mergers between clusters and their neighbors are considered. Therefore, GGC has a nearly linear computational complexity with respect to the number of samples. Also, unlike other algorithms, due to the greedy strategy, the solution of the proposed algorithm is unique. In other words, its performance is not affected by randomness. We apply the proposed method to solve the problem of normalized cut which is a widely concerned graph cut problem. Extensive experiments show that better solutions can often be achieved compared to the traditional two-stage optimization algorithm (eigendecomposition + k-means), on the normalized cut problem. In addition, the performance of GGC also has advantages compared to several state-of-the-art clustering algorithms.
Clustering Based on Density Propagation and Subcluster Merging
Nov 04, 2024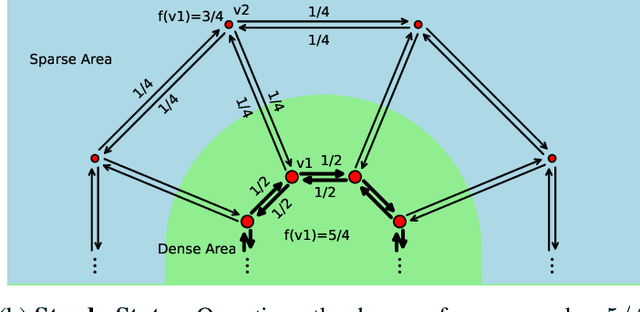
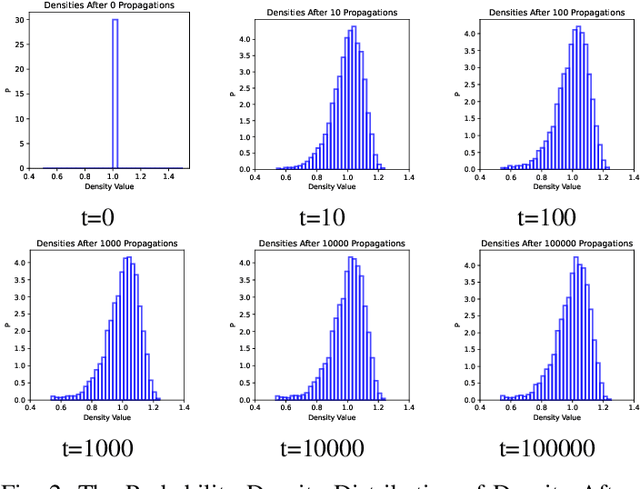
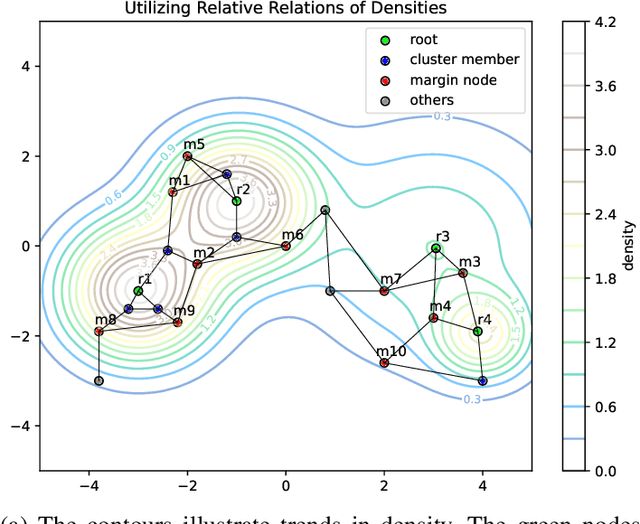
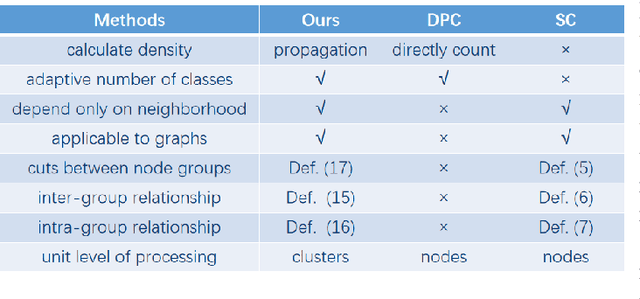
Abstract:We propose the DPSM method, a density-based node clustering approach that automatically determines the number of clusters and can be applied in both data space and graph space. Unlike traditional density-based clustering methods, which necessitate calculating the distance between any two nodes, our proposed technique determines density through a propagation process, thereby making it suitable for a graph space. In DPSM, nodes are partitioned into small clusters based on propagated density. The partitioning technique has been proved to be sound and complete. We then extend the concept of spectral clustering from individual nodes to these small clusters, while introducing the CluCut measure to guide cluster merging. This measure is modified in various ways to account for cluster properties, thus provides guidance on when to terminate the merging process. Various experiments have validated the effectiveness of DOSM and the accuracy of these conclusions.
Fast Semi-supervised Learning on Large Graphs: An Improved Green-function Method
Nov 04, 2024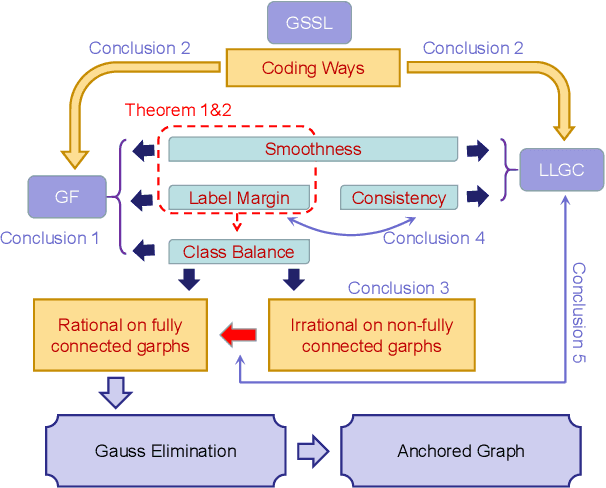

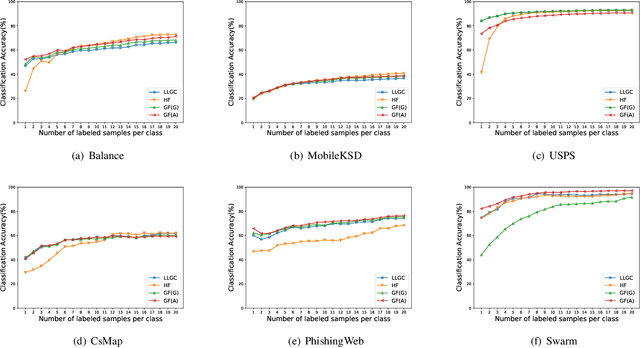
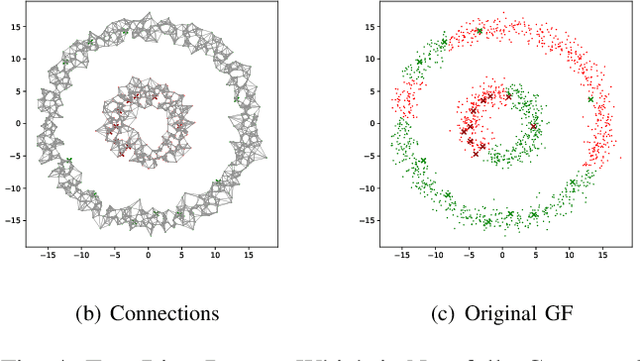
Abstract:In the graph-based semi-supervised learning, the Green-function method is a classical method that works by computing the Green's function in the graph space. However, when applied to large graphs, especially those sparse ones, this method performs unstably and unsatisfactorily. We make a detailed analysis on it and propose a novel method from the perspective of optimization. On fully connected graphs, the method is equivalent to the Green-function method and can be seen as another interpretation with physical meanings, while on non-fully connected graphs, it helps to explain why the Green-function method causes a mess on large sparse graphs. To solve this dilemma, we propose a workable approach to improve our proposed method. Unlike the original method, our improved method can also apply two accelerating techniques, Gaussian Elimination, and Anchored Graphs to become more efficient on large graphs. Finally, the extensive experiments prove our conclusions and the efficiency, accuracy, and stability of our improved Green's function method.
PRformer: Pyramidal Recurrent Transformer for Multivariate Time Series Forecasting
Aug 20, 2024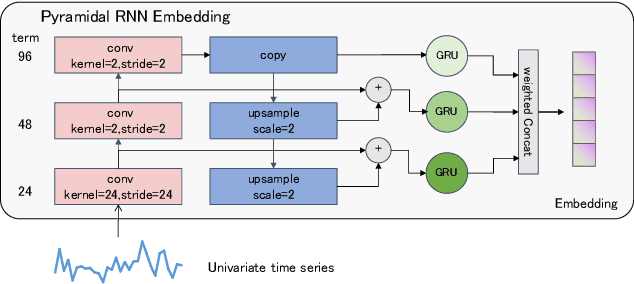
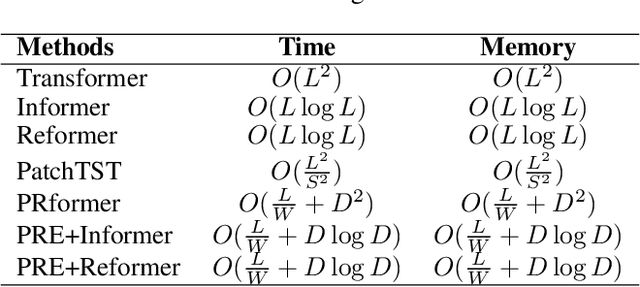
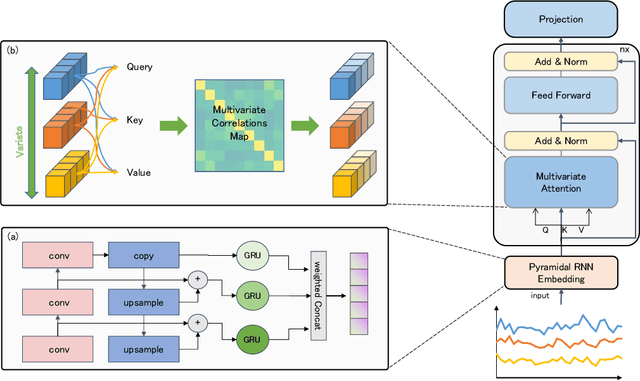

Abstract:The self-attention mechanism in Transformer architecture, invariant to sequence order, necessitates positional embeddings to encode temporal order in time series prediction. We argue that this reliance on positional embeddings restricts the Transformer's ability to effectively represent temporal sequences, particularly when employing longer lookback windows. To address this, we introduce an innovative approach that combines Pyramid RNN embeddings(PRE) for univariate time series with the Transformer's capability to model multivariate dependencies. PRE, utilizing pyramidal one-dimensional convolutional layers, constructs multiscale convolutional features that preserve temporal order. Additionally, RNNs, layered atop these features, learn multiscale time series representations sensitive to sequence order. This integration into Transformer models with attention mechanisms results in significant performance enhancements. We present the PRformer, a model integrating PRE with a standard Transformer encoder, demonstrating state-of-the-art performance on various real-world datasets. This performance highlights the effectiveness of our approach in leveraging longer lookback windows and underscores the critical role of robust temporal representations in maximizing Transformer's potential for prediction tasks. Code is available at this repository: \url{https://github.com/usualheart/PRformer}.
Doubly Stochastic Adaptive Neighbors Clustering via the Marcus Mapping
Aug 06, 2024

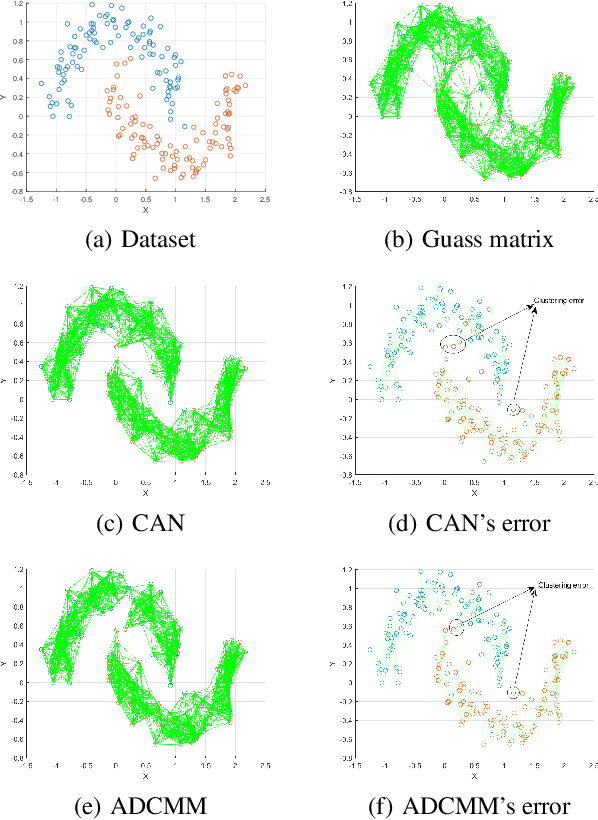
Abstract:Clustering is a fundamental task in machine learning and data science, and similarity graph-based clustering is an important approach within this domain. Doubly stochastic symmetric similarity graphs provide numerous benefits for clustering problems and downstream tasks, yet learning such graphs remains a significant challenge. Marcus theorem states that a strictly positive symmetric matrix can be transformed into a doubly stochastic symmetric matrix by diagonal matrices. However, in clustering, learning sparse matrices is crucial for computational efficiency. We extend Marcus theorem by proposing the Marcus mapping, which indicates that certain sparse matrices can also be transformed into doubly stochastic symmetric matrices via diagonal matrices. Additionally, we introduce rank constraints into the clustering problem and propose the Doubly Stochastic Adaptive Neighbors Clustering algorithm based on the Marcus Mapping (ANCMM). This ensures that the learned graph naturally divides into the desired number of clusters. We validate the effectiveness of our algorithm through extensive comparisons with state-of-the-art algorithms. Finally, we explore the relationship between the Marcus mapping and optimal transport. We prove that the Marcus mapping solves a specific type of optimal transport problem and demonstrate that solving this problem through Marcus mapping is more efficient than directly applying optimal transport methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge