Anup Teejo Mathew
Dynamic Manipulation of Deformable Objects in 3D: Simulation, Benchmark and Learning Strategy
May 23, 2025Abstract:Goal-conditioned dynamic manipulation is inherently challenging due to complex system dynamics and stringent task constraints, particularly in deformable object scenarios characterized by high degrees of freedom and underactuation. Prior methods often simplify the problem to low-speed or 2D settings, limiting their applicability to real-world 3D tasks. In this work, we explore 3D goal-conditioned rope manipulation as a representative challenge. To mitigate data scarcity, we introduce a novel simulation framework and benchmark grounded in reduced-order dynamics, which enables compact state representation and facilitates efficient policy learning. Building on this, we propose Dynamics Informed Diffusion Policy (DIDP), a framework that integrates imitation pretraining with physics-informed test-time adaptation. First, we design a diffusion policy that learns inverse dynamics within the reduced-order space, enabling imitation learning to move beyond na\"ive data fitting and capture the underlying physical structure. Second, we propose a physics-informed test-time adaptation scheme that imposes kinematic boundary conditions and structured dynamics priors on the diffusion process, ensuring consistency and reliability in manipulation execution. Extensive experiments validate the proposed approach, demonstrating strong performance in terms of accuracy and robustness in the learned policy.
ZodiAq: An Isotropic Flagella-Inspired Soft Underwater Drone for Safe Marine Exploration
Mar 25, 2025

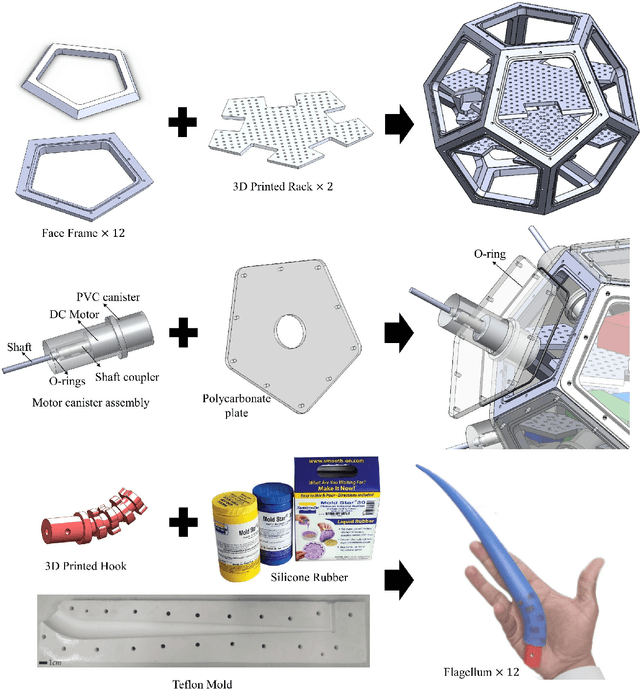

Abstract:The inherent challenges of robotic underwater exploration, such as hydrodynamic effects, the complexity of dynamic coupling, and the necessity for sensitive interaction with marine life, call for the adoption of soft robotic approaches in marine exploration. To address this, we present a novel prototype, ZodiAq, a soft underwater drone inspired by prokaryotic bacterial flagella. ZodiAq's unique dodecahedral structure, equipped with 12 flagella-like arms, ensures design redundancy and compliance, ideal for navigating complex underwater terrains. The prototype features a central unit based on a Raspberry Pi, connected to a sensory system for inertial, depth, and vision detection, and an acoustic modem for communication. Combined with the implemented control law, it renders ZodiAq an intelligent system. This paper details the design and fabrication process of ZodiAq, highlighting design choices and prototype capabilities. Based on the strain-based modeling of Cosserat rods, we have developed a digital twin of the prototype within a simulation toolbox to ease analysis and control. To optimize its operation in dynamic aquatic conditions, a simplified model-based controller has been developed and implemented, facilitating intelligent and adaptive movement in the hydrodynamic environment. Extensive experimental demonstrations highlight the drone's potential, showcasing its design redundancy, embodied intelligence, crawling gait, and practical applications in diverse underwater settings. This research contributes significantly to the field of underwater soft robotics, offering a promising new avenue for safe, efficient, and environmentally conscious underwater exploration.
Real-time Dynamics of Soft Manipulators with Cross-section Inflation: Application to the Octopus Muscular Hydrostat
Dec 04, 2024Abstract:Inspired by the embodied intelligence of biological creatures like the octopus, the soft robotic arm utilizes its highly flexible structure to perform various tasks in the complex environment. While the classic Cosserat rod theory investigates the bending, twisting, shearing, and stretching of the soft arm, it fails to capture the in-plane deformation that occurs during certain tasks, particularly those involving active lateral traction. This paper introduces an extended Cosserat rod theory addressing these limitations by incorporating an extra strain variable reflecting the in-plane inflation ratio. To accurately describe the viscoelasticity effect of the soft body in dynamics, the proposed model enhances the constitutive law by integrating the Saint-Venant Kirchhoff hyperelastic and Kelvin-Voigt viscous models. The active and environmental loads are accounted for the equations of motion, which are numerically solved by adapting the Geometric Variable Strain (GVS) approach to balance the accuracy and computational efficiency. Our contributions include the derivation of the extended Cosserat rod theory in dynamic context, and the development of a reduced-order numerical method that enables rapid and precise solutions. We demonstrate applications of the model in stiffness tuning of a soft robotic arm and the study of complex octopus' arm motions.
Analytical Derivatives for Efficient Mechanical Simulations of Hybrid Soft Rigid Robots
Nov 07, 2024Abstract:Algorithms that use derivatives of governing equations have accelerated rigid robot simulations and improved their accuracy, enabling the modeling of complex, real-world capabilities. However, extending these methods to soft and hybrid soft-rigid robots is significantly more challenging due to the complexities in modeling continuous deformations inherent in soft bodies. A considerable number of soft robots and the deformable links of hybrid robots can be effectively modeled as slender rods. The Geometric Variable Strain (GVS) model, which employs the screw theory and the strain parameterization of the Cosserat rod, extends the rod theory to model hybrid soft-rigid robots within the same mathematical framework. Using the Recursive Newton-Euler Algorithm, we developed the analytical derivatives of the governing equations of the GVS model. These derivatives facilitate the implicit integration of dynamics and provide the analytical Jacobian of the statics residue, ensuring fast and accurate computations. We applied these derivatives to the mechanical simulations of six common robotic systems: a soft cable-driven manipulator, a hybrid serial robot, a fin-ray finger, a hybrid parallel robot, a contact scenario, and an underwater hybrid mobile robot. Simulation results demonstrate substantial improvements in computational efficiency, with speed-ups of up to three orders of magnitude. We validate the model by comparing simulations done with and without analytical derivatives. Beyond static and dynamic simulations, the techniques discussed in this paper hold the potential to revolutionize the analysis, control, and optimization of hybrid robotic systems for real-world applications.
Soft Synergies: Model Order Reduction of Hybrid Soft-Rigid Robots via Optimal Strain Parameterization
May 21, 2024



Abstract:Soft robots offer remarkable adaptability and safety advantages over rigid robots, but modeling their complex, nonlinear dynamics remains challenging. Strain-based models have recently emerged as a promising candidate to describe such systems, however, they tend to be high-dimensional and time consuming. This paper presents a novel model order reduction approach for soft and hybrid robots by combining strain-based modeling with Proper Orthogonal Decomposition (POD). The method identifies optimal coupled strain basis functions -- or mechanical synergies -- from simulation data, enabling the description of soft robot configurations with a minimal number of generalized coordinates. The reduced order model (ROM) achieves substantial dimensionality reduction while preserving accuracy. Rigorous testing demonstrates the interpolation and extrapolation capabilities of the ROM for soft manipulators under static and dynamic conditions. The approach is further validated on a snake-like hyper-redundant rigid manipulator and a closed-chain system with soft and rigid components, illustrating its broad applicability. Finally, the approach is leveraged for shape estimation of a real six-actuator soft manipulator using only two position markers, showcasing its practical utility. This POD-based ROM offers significant computational speed-ups, paving the way for real-time simulation and control of complex soft and hybrid robots.
Soft Robots Modeling: a Literature Unwinding
Dec 07, 2021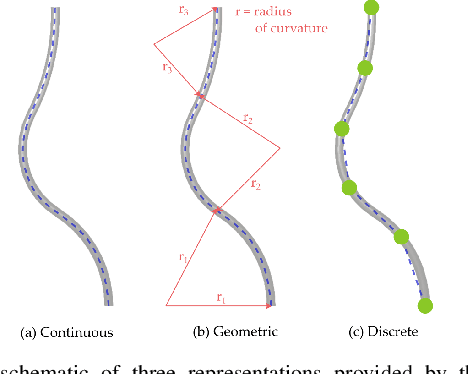

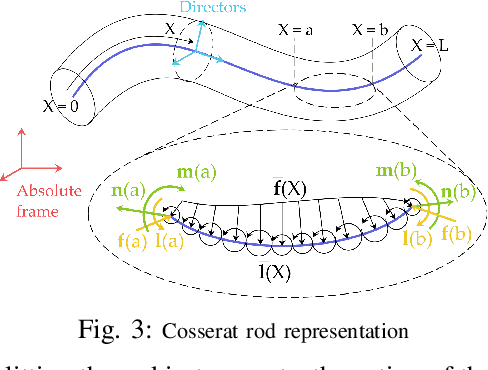
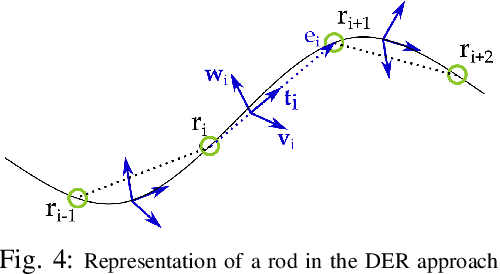
Abstract:The robotics community has seen an exponential growth in the level of complexity of the theoretical tools presented for the modeling of soft robotics devices. Different solutions have been presented to overcome the difficulties related to the modeling of soft robots, often leveraging on other scientific disciplines, such as continuum mechanics and computer graphics. These theoretical foundations are often taken for granted and this lead to an intricate literature that, consequently, has never been the subject of a complete review. Withing this scenario, the objective of the presented paper is twofold. The common theoretical roots that relate the different families of modeling techniques are highlighted, employing a unifying language that ease the analysis of their main connections and differences. Thus, the listing of the approaches naturally follows and a complete, untangled, review of the main works on the field is finally provided.
SoRoSim: a MATLAB Toolbox for Soft Robotics Based on the Geometric Variable-strain Approach
Jul 12, 2021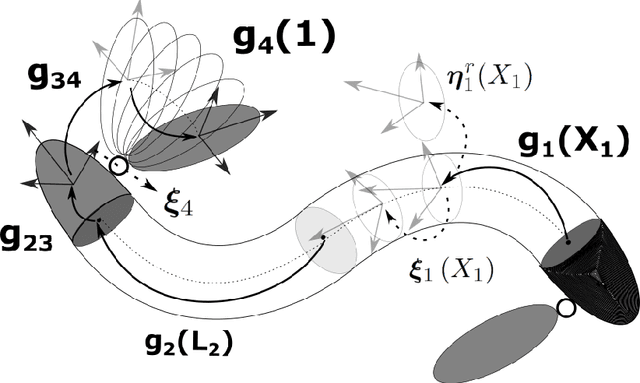



Abstract:Soft robotics has been a trending topic within the robotics community for almost two decades. However, the available tools for the community to model and analyze soft robotics artifacts are still limited. This paper presents the development of a user-friendly MATLAB toolbox, SoRoSim, that integrates the Geometric Variable Strain model to facilitate the modeling, analysis, and simulation of hybrid rigid-soft open-chain robotic systems. The toolbox implements a recursive, two-level nested quadrature scheme to solve the model. We demonstrate several examples and applications to validate the toolbox and explore the toolbox's capabilities to efficiently model a vast range of robotic systems, considering different actuators and external loads, including the fluid-structure interactions. We think that the soft-robotics research community will benefit from the SoRoSim toolbox for a wide variety of applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge