Analytical Derivatives for Efficient Mechanical Simulations of Hybrid Soft Rigid Robots

Algorithms that use derivatives of governing equations have accelerated rigid robot simulations and improved their accuracy, enabling the modeling of complex, real-world capabilities. However, extending these methods to soft and hybrid soft-rigid robots is significantly more challenging due to the complexities in modeling continuous deformations inherent in soft bodies. A considerable number of soft robots and the deformable links of hybrid robots can be effectively modeled as slender rods. The Geometric Variable Strain (GVS) model, which employs the screw theory and the strain parameterization of the Cosserat rod, extends the rod theory to model hybrid soft-rigid robots within the same mathematical framework. Using the Recursive Newton-Euler Algorithm, we developed the analytical derivatives of the governing equations of the GVS model. These derivatives facilitate the implicit integration of dynamics and provide the analytical Jacobian of the statics residue, ensuring fast and accurate computations. We applied these derivatives to the mechanical simulations of six common robotic systems: a soft cable-driven manipulator, a hybrid serial robot, a fin-ray finger, a hybrid parallel robot, a contact scenario, and an underwater hybrid mobile robot. Simulation results demonstrate substantial improvements in computational efficiency, with speed-ups of up to three orders of magnitude. We validate the model by comparing simulations done with and without analytical derivatives. Beyond static and dynamic simulations, the techniques discussed in this paper hold the potential to revolutionize the analysis, control, and optimization of hybrid robotic systems for real-world applications.

SoRoSim: a MATLAB Toolbox for Soft Robotics Based on the Geometric Variable-strain Approach

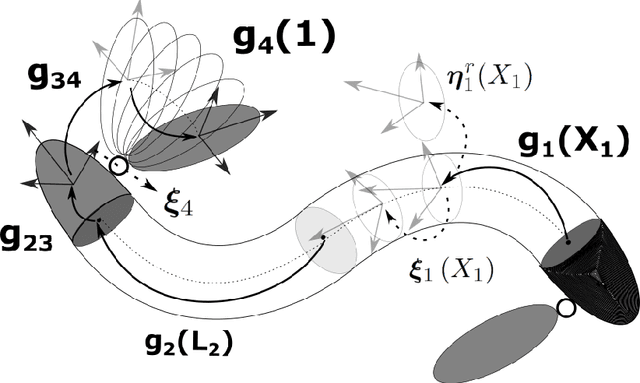
Soft robotics has been a trending topic within the robotics community for almost two decades. However, the available tools for the community to model and analyze soft robotics artifacts are still limited. This paper presents the development of a user-friendly MATLAB toolbox, SoRoSim, that integrates the Geometric Variable Strain model to facilitate the modeling, analysis, and simulation of hybrid rigid-soft open-chain robotic systems. The toolbox implements a recursive, two-level nested quadrature scheme to solve the model. We demonstrate several examples and applications to validate the toolbox and explore the toolbox's capabilities to efficiently model a vast range of robotic systems, considering different actuators and external loads, including the fluid-structure interactions. We think that the soft-robotics research community will benefit from the SoRoSim toolbox for a wide variety of applications.

Discrete Cosserat Approach for Multi-Section Soft Robots Dynamics

In spite of recent progress, soft robotics still suffers from a lack of unified modeling framework. Nowadays, the most adopted model for the design and control of soft robots is the piece-wise constant curvature model, with its consolidated benefits and drawbacks. In this work, an alternative model for multisection soft robots dynamics is presented based on a discrete Cosserat approach, which, not only takes into account shear and torsional deformations, essentials to cope with out-of-plane external loads, but also inherits the geometrical and mechanical properties of the continuous Cosserat model, making it the natural soft robotics counterpart of the traditional rigid robotics dynamics model. The soundness of the model is demonstrated through extensive simulation and experimental results for both plane and out-of-plane motions.