Riemannian Optimization on Relaxed Indicator Matrix Manifold

The indicator matrix plays an important role in machine learning, but optimizing it is an NP-hard problem. We propose a new relaxation of the indicator matrix and prove that this relaxation forms a manifold, which we call the Relaxed Indicator Matrix Manifold (RIM manifold). Based on Riemannian geometry, we develop a Riemannian toolbox for optimization on the RIM manifold. Specifically, we provide several methods of Retraction, including a fast Retraction method to obtain geodesics. We point out that the RIM manifold is a generalization of the double stochastic manifold, and it is much faster than existing methods on the double stochastic manifold, which has a complexity of \( \mathcal{O}(n^3) \), while RIM manifold optimization is \( \mathcal{O}(n) \) and often yields better results. We conducted extensive experiments, including image denoising, with millions of variables to support our conclusion, and applied the RIM manifold to Ratio Cut, achieving clustering results that outperform the state-of-the-art methods. Our Code in \href{https://github.com/Yuan-Jinghui/Riemannian-Optimization-on-Relaxed-Indicator-Matrix-Manifold}{https://github.com/Yuan-Jinghui/Riemannian-Optimization-on-Relaxed-Indicator-Matrix-Manifold}.

Dual-Bounded Nonlinear Optimal Transport for Size Constrained Min Cut Clustering

Min cut is an important graph partitioning method. However, current solutions to the min cut problem suffer from slow speeds, difficulty in solving, and often converge to simple solutions. To address these issues, we relax the min cut problem into a dual-bounded constraint and, for the first time, treat the min cut problem as a dual-bounded nonlinear optimal transport problem. Additionally, we develop a method for solving dual-bounded nonlinear optimal transport based on the Frank-Wolfe method (abbreviated as DNF). Notably, DNF not only solves the size constrained min cut problem but is also applicable to all dual-bounded nonlinear optimal transport problems. We prove that for convex problems satisfying Lipschitz smoothness, the DNF method can achieve a convergence rate of \(\mathcal{O}(\frac{1}{t})\). We apply the DNF method to the min cut problem and find that it achieves state-of-the-art performance in terms of both the loss function and clustering accuracy at the fastest speed, with a convergence rate of \(\mathcal{O}(\frac{1}{\sqrt{t}})\). Moreover, the DNF method for the size constrained min cut problem requires no parameters and exhibits better stability.

Doubly Stochastic Adaptive Neighbors Clustering via the Marcus Mapping

Clustering is a fundamental task in machine learning and data science, and similarity graph-based clustering is an important approach within this domain. Doubly stochastic symmetric similarity graphs provide numerous benefits for clustering problems and downstream tasks, yet learning such graphs remains a significant challenge. Marcus theorem states that a strictly positive symmetric matrix can be transformed into a doubly stochastic symmetric matrix by diagonal matrices. However, in clustering, learning sparse matrices is crucial for computational efficiency. We extend Marcus theorem by proposing the Marcus mapping, which indicates that certain sparse matrices can also be transformed into doubly stochastic symmetric matrices via diagonal matrices. Additionally, we introduce rank constraints into the clustering problem and propose the Doubly Stochastic Adaptive Neighbors Clustering algorithm based on the Marcus Mapping (ANCMM). This ensures that the learned graph naturally divides into the desired number of clusters. We validate the effectiveness of our algorithm through extensive comparisons with state-of-the-art algorithms. Finally, we explore the relationship between the Marcus mapping and optimal transport. We prove that the Marcus mapping solves a specific type of optimal transport problem and demonstrate that solving this problem through Marcus mapping is more efficient than directly applying optimal transport methods.

Achieving More with Less: A Tensor-Optimization-Powered Ensemble Method

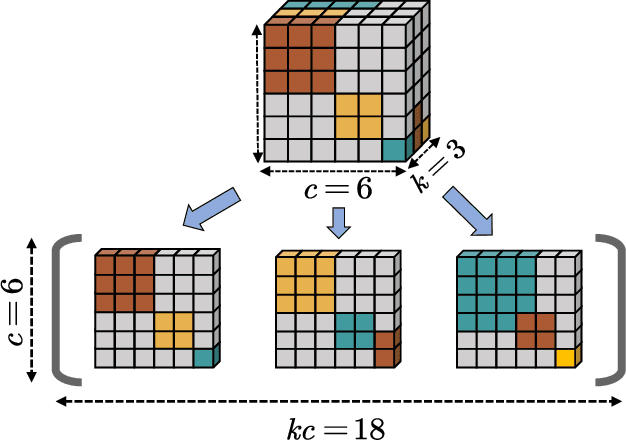
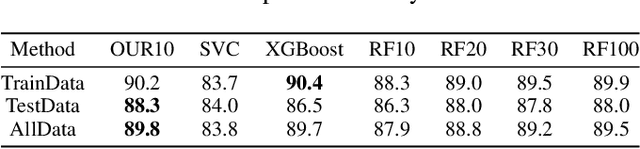
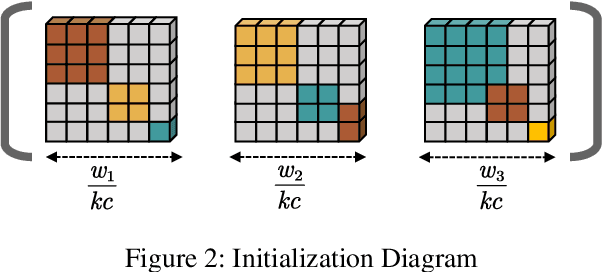
Ensemble learning is a method that leverages weak learners to produce a strong learner. However, obtaining a large number of base learners requires substantial time and computational resources. Therefore, it is meaningful to study how to achieve the performance typically obtained with many base learners using only a few. We argue that to achieve this, it is essential to enhance both classification performance and generalization ability during the ensemble process. To increase model accuracy, each weak base learner needs to be more efficiently integrated. It is observed that different base learners exhibit varying levels of accuracy in predicting different classes. To capitalize on this, we introduce confidence tensors $\tilde{\mathbf{\Theta}}$ and $\tilde{\mathbf{\Theta}}_{rst}$ signifies that the $t$-th base classifier assigns the sample to class $r$ while it actually belongs to class $s$. To the best of our knowledge, this is the first time an evaluation of the performance of base classifiers across different classes has been proposed. The proposed confidence tensor compensates for the strengths and weaknesses of each base classifier in different classes, enabling the method to achieve superior results with a smaller number of base learners. To enhance generalization performance, we design a smooth and convex objective function that leverages the concept of margin, making the strong learner more discriminative. Furthermore, it is proved that in gradient matrix of the loss function, the sum of each column's elements is zero, allowing us to solve a constrained optimization problem using gradient-based methods. We then compare our algorithm with random forests of ten times the size and other classical methods across numerous datasets, demonstrating the superiority of our approach.