Achieving More with Less: A Tensor-Optimization-Powered Ensemble Method
Paper and Code
Aug 06, 2024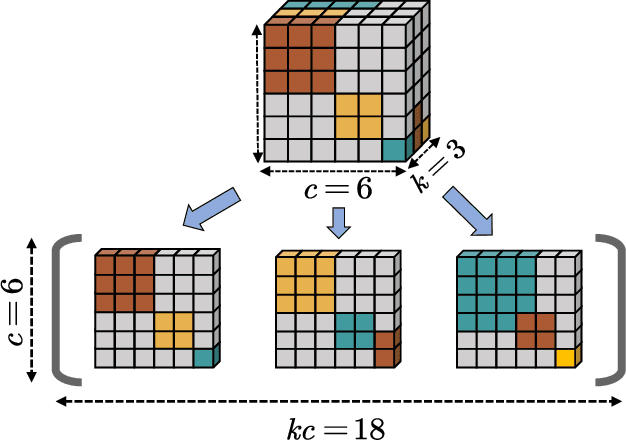
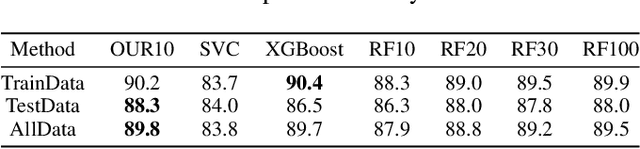
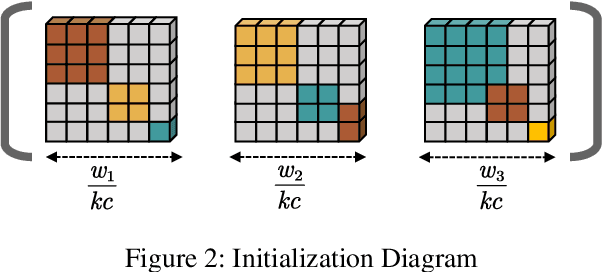
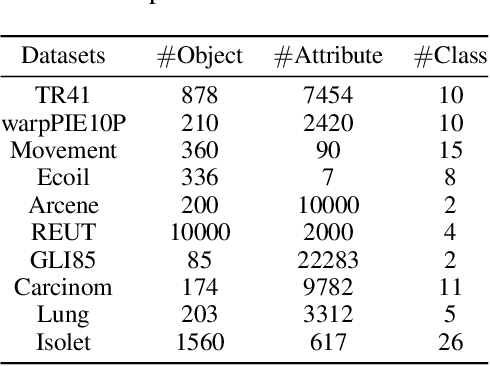
Ensemble learning is a method that leverages weak learners to produce a strong learner. However, obtaining a large number of base learners requires substantial time and computational resources. Therefore, it is meaningful to study how to achieve the performance typically obtained with many base learners using only a few. We argue that to achieve this, it is essential to enhance both classification performance and generalization ability during the ensemble process. To increase model accuracy, each weak base learner needs to be more efficiently integrated. It is observed that different base learners exhibit varying levels of accuracy in predicting different classes. To capitalize on this, we introduce confidence tensors $\tilde{\mathbf{\Theta}}$ and $\tilde{\mathbf{\Theta}}_{rst}$ signifies that the $t$-th base classifier assigns the sample to class $r$ while it actually belongs to class $s$. To the best of our knowledge, this is the first time an evaluation of the performance of base classifiers across different classes has been proposed. The proposed confidence tensor compensates for the strengths and weaknesses of each base classifier in different classes, enabling the method to achieve superior results with a smaller number of base learners. To enhance generalization performance, we design a smooth and convex objective function that leverages the concept of margin, making the strong learner more discriminative. Furthermore, it is proved that in gradient matrix of the loss function, the sum of each column's elements is zero, allowing us to solve a constrained optimization problem using gradient-based methods. We then compare our algorithm with random forests of ten times the size and other classical methods across numerous datasets, demonstrating the superiority of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge