Fast Semi-supervised Learning on Large Graphs: An Improved Green-function Method

In the graph-based semi-supervised learning, the Green-function method is a classical method that works by computing the Green's function in the graph space. However, when applied to large graphs, especially those sparse ones, this method performs unstably and unsatisfactorily. We make a detailed analysis on it and propose a novel method from the perspective of optimization. On fully connected graphs, the method is equivalent to the Green-function method and can be seen as another interpretation with physical meanings, while on non-fully connected graphs, it helps to explain why the Green-function method causes a mess on large sparse graphs. To solve this dilemma, we propose a workable approach to improve our proposed method. Unlike the original method, our improved method can also apply two accelerating techniques, Gaussian Elimination, and Anchored Graphs to become more efficient on large graphs. Finally, the extensive experiments prove our conclusions and the efficiency, accuracy, and stability of our improved Green's function method.

Clustering Based on Density Propagation and Subcluster Merging

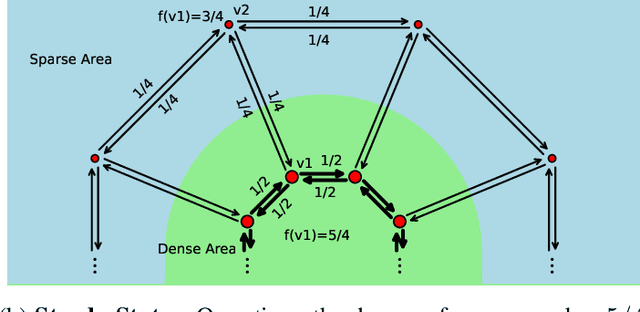
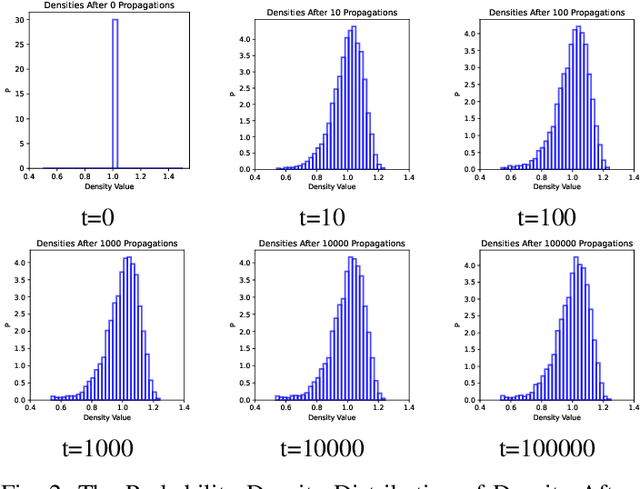
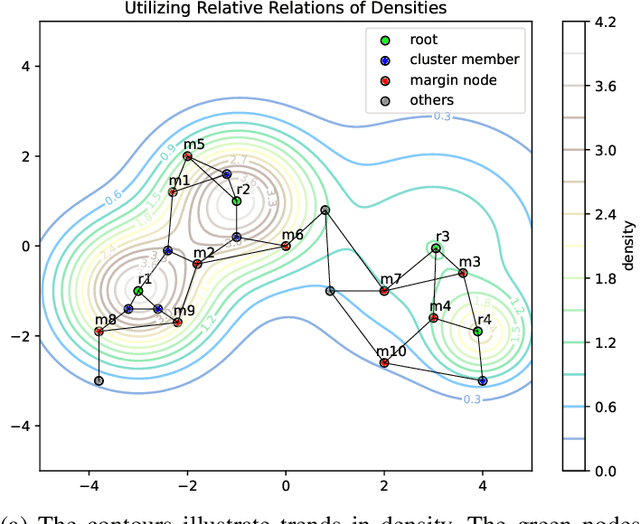
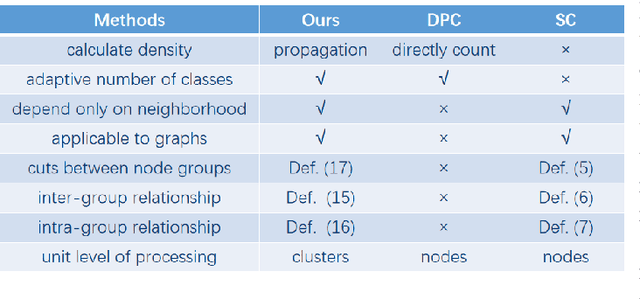
We propose the DPSM method, a density-based node clustering approach that automatically determines the number of clusters and can be applied in both data space and graph space. Unlike traditional density-based clustering methods, which necessitate calculating the distance between any two nodes, our proposed technique determines density through a propagation process, thereby making it suitable for a graph space. In DPSM, nodes are partitioned into small clusters based on propagated density. The partitioning technique has been proved to be sound and complete. We then extend the concept of spectral clustering from individual nodes to these small clusters, while introducing the CluCut measure to guide cluster merging. This measure is modified in various ways to account for cluster properties, thus provides guidance on when to terminate the merging process. Various experiments have validated the effectiveness of DOSM and the accuracy of these conclusions.