Fahira Afzal Maken
GS-2DGS: Geometrically Supervised 2DGS for Reflective Object Reconstruction
Jun 16, 2025Abstract:3D modeling of highly reflective objects remains challenging due to strong view-dependent appearances. While previous SDF-based methods can recover high-quality meshes, they are often time-consuming and tend to produce over-smoothed surfaces. In contrast, 3D Gaussian Splatting (3DGS) offers the advantage of high speed and detailed real-time rendering, but extracting surfaces from the Gaussians can be noisy due to the lack of geometric constraints. To bridge the gap between these approaches, we propose a novel reconstruction method called GS-2DGS for reflective objects based on 2D Gaussian Splatting (2DGS). Our approach combines the rapid rendering capabilities of Gaussian Splatting with additional geometric information from foundation models. Experimental results on synthetic and real datasets demonstrate that our method significantly outperforms Gaussian-based techniques in terms of reconstruction and relighting and achieves performance comparable to SDF-based methods while being an order of magnitude faster. Code is available at https://github.com/hirotong/GS2DGS
Grasping by parallel shape matching
Dec 11, 2024



Abstract:Grasping is essential in robotic manipulation, yet challenging due to object and gripper diversity and real-world complexities. Traditional analytic approaches often have long optimization times, while data-driven methods struggle with unseen objects. This paper formulates the problem as a rigid shape matching between gripper and object, which optimizes with Annealed Stein Iterative Closest Point (AS-ICP) and leverages GPU-based parallelization. By incorporating the gripper's tool center point and the object's center of mass into the cost function and using a signed distance field of the gripper for collision checking, our method achieves robust grasps with low computational time. Experiments with the Kinova KG3 gripper show an 87.3% success rate and 0.926 s computation time across various objects and settings, highlighting its potential for real-world applications.
Homography Guided Temporal Fusion for Road Line and Marking Segmentation
Apr 11, 2024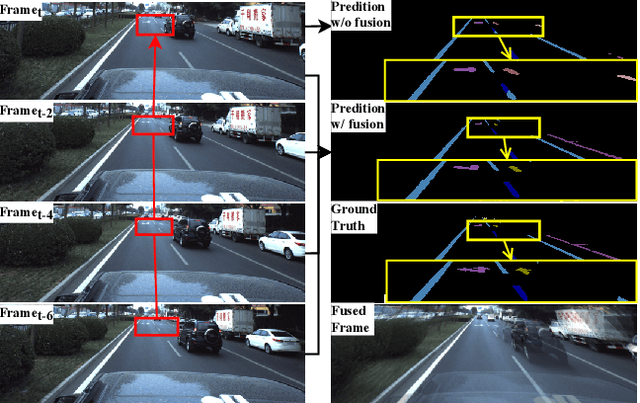
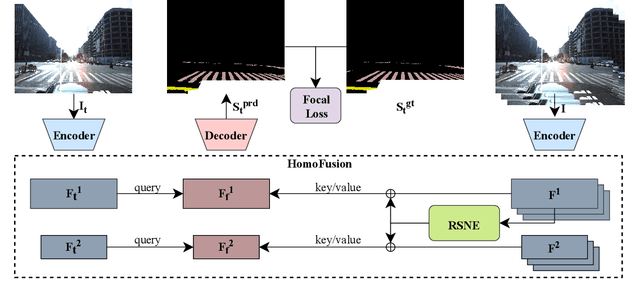


Abstract:Reliable segmentation of road lines and markings is critical to autonomous driving. Our work is motivated by the observations that road lines and markings are (1) frequently occluded in the presence of moving vehicles, shadow, and glare and (2) highly structured with low intra-class shape variance and overall high appearance consistency. To solve these issues, we propose a Homography Guided Fusion (HomoFusion) module to exploit temporally-adjacent video frames for complementary cues facilitating the correct classification of the partially occluded road lines or markings. To reduce computational complexity, a novel surface normal estimator is proposed to establish spatial correspondences between the sampled frames, allowing the HomoFusion module to perform a pixel-to-pixel attention mechanism in updating the representation of the occluded road lines or markings. Experiments on ApolloScape, a large-scale lane mark segmentation dataset, and ApolloScape Night with artificial simulated night-time road conditions, demonstrate that our method outperforms other existing SOTA lane mark segmentation models with less than 9\% of their parameters and computational complexity. We show that exploiting available camera intrinsic data and ground plane assumption for cross-frame correspondence can lead to a light-weight network with significantly improved performances in speed and accuracy. We also prove the versatility of our HomoFusion approach by applying it to the problem of water puddle segmentation and achieving SOTA performance.
Seeing Through the Glass: Neural 3D Reconstruction of Object Inside a Transparent Container
Mar 24, 2023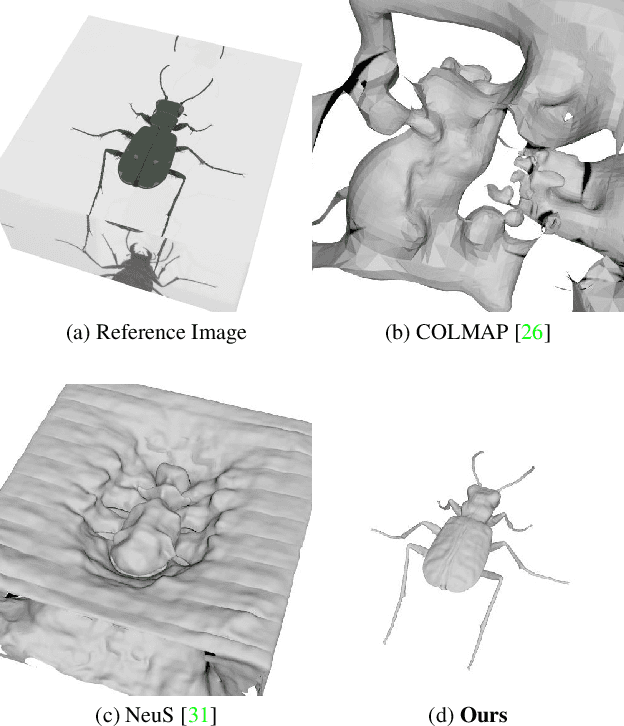
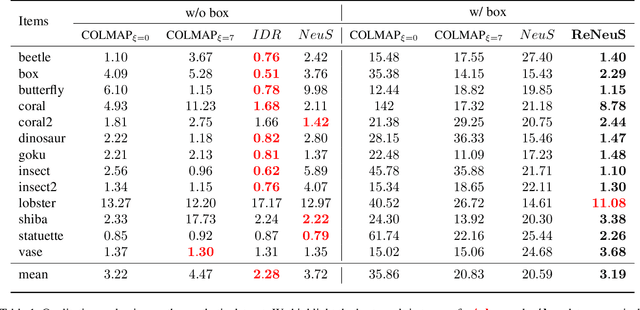
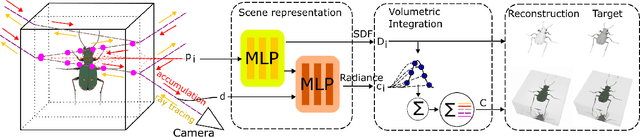

Abstract:In this paper, we define a new problem of recovering the 3D geometry of an object confined in a transparent enclosure. We also propose a novel method for solving this challenging problem. Transparent enclosures pose challenges of multiple light reflections and refractions at the interface between different propagation media e.g. air or glass. These multiple reflections and refractions cause serious image distortions which invalidate the single viewpoint assumption. Hence the 3D geometry of such objects cannot be reliably reconstructed using existing methods, such as traditional structure from motion or modern neural reconstruction methods. We solve this problem by explicitly modeling the scene as two distinct sub-spaces, inside and outside the transparent enclosure. We use an existing neural reconstruction method (NeuS) that implicitly represents the geometry and appearance of the inner subspace. In order to account for complex light interactions, we develop a hybrid rendering strategy that combines volume rendering with ray tracing. We then recover the underlying geometry and appearance of the model by minimizing the difference between the real and hybrid rendered images. We evaluate our method on both synthetic and real data. Experiment results show that our method outperforms the state-of-the-art (SOTA) methods. Codes and data will be available at https://github.com/hirotong/ReNeuS
Stein Particle Filter for Nonlinear, Non-Gaussian State Estimation
Feb 09, 2022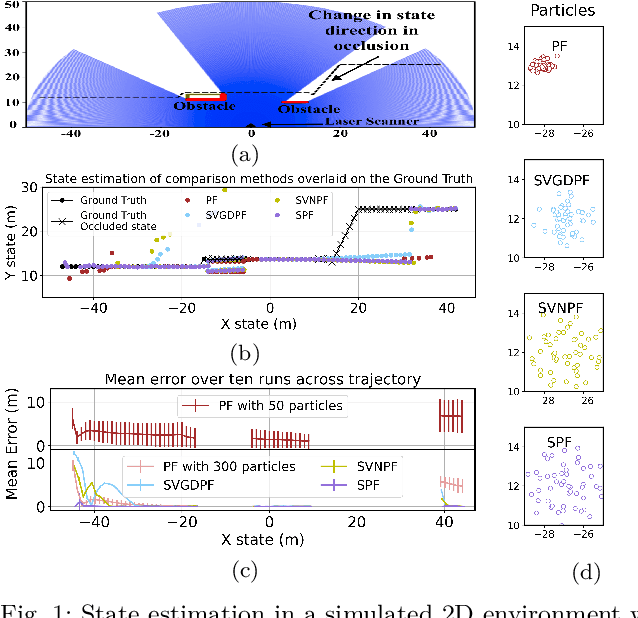
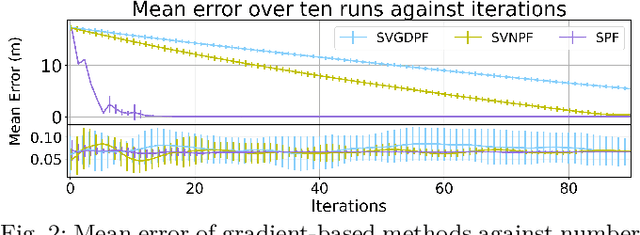
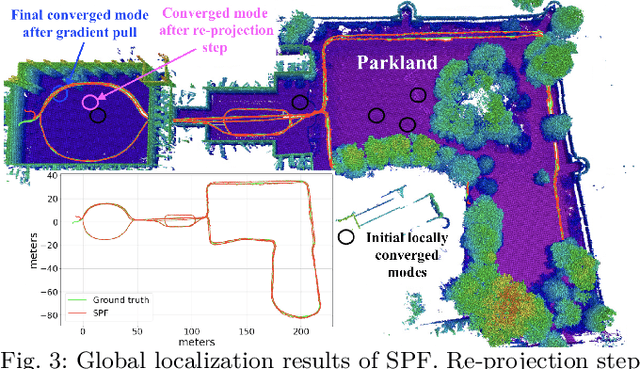
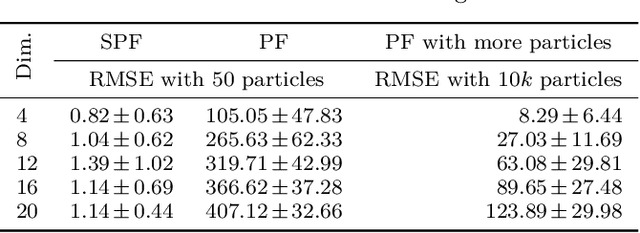
Abstract:Estimation of a dynamical system's latent state subject to sensor noise and model inaccuracies remains a critical yet difficult problem in robotics. While Kalman filters provide the optimal solution in the least squared sense for linear and Gaussian noise problems, the general nonlinear and non-Gaussian noise case is significantly more complicated, typically relying on sampling strategies that are limited to low-dimensional state spaces. In this paper we devise a general inference procedure for filtering of nonlinear, non-Gaussian dynamical systems that exploits the differentiability of both the update and prediction models to scale to higher dimensional spaces. Our method, Stein particle filter, can be seen as a deterministic flow of particles, embedded in a reproducing kernel Hilbert space, from an initial state to the desirable posterior. The particles evolve jointly to conform to a posterior approximation while interacting with each other through a repulsive force. We evaluate the method in simulation and in complex localization tasks while comparing it to sequential Monte Carlo solutions.
* 8 pages, 3 figures, Robotics and Automation Letters
Stein ICP for Uncertainty Estimation in Point Cloud Matching
Jun 07, 2021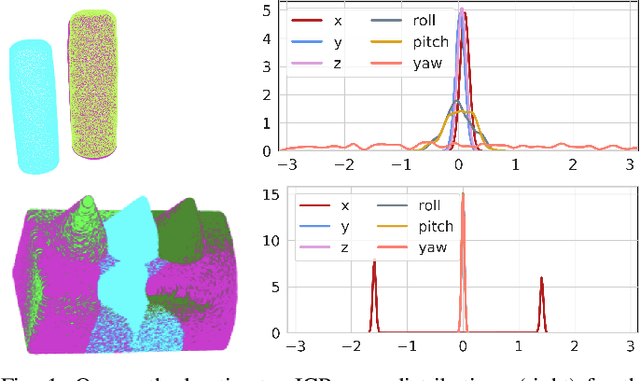

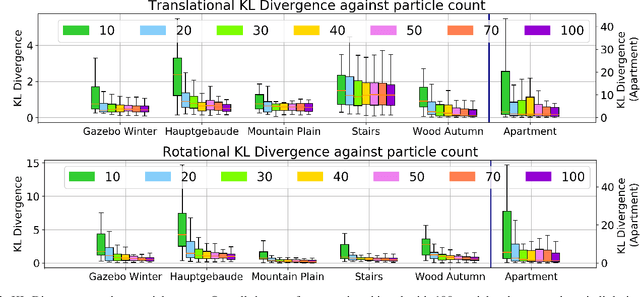

Abstract:Quantification of uncertainty in point cloud matching is critical in many tasks such as pose estimation, sensor fusion, and grasping. Iterative closest point (ICP) is a commonly used pose estimation algorithm which provides a point estimate of the transformation between two point clouds. There are many sources of uncertainty in this process that may arise due to sensor noise, ambiguous environment, and occlusion. However, for safety critical problems such as autonomous driving, a point estimate of the pose transformation is not sufficient as it does not provide information about the multiple solutions. Current probabilistic ICP methods usually do not capture all sources of uncertainty and may provide unreliable transformation estimates which can have a detrimental effect in state estimation or decision making tasks that use this information. In this work we propose a new algorithm to align two point clouds that can precisely estimate the uncertainty of ICP's transformation parameters. We develop a Stein variational inference framework with gradient based optimization of ICP's cost function. The method provides a non-parametric estimate of the transformation, can model complex multi-modal distributions, and can be effectively parallelized on a GPU. Experiments using 3D kinect data as well as sparse indoor/outdoor LiDAR data show that our method is capable of efficiently producing accurate pose uncertainty estimates.
Estimating Motion Uncertainty with Bayesian ICP
Apr 16, 2020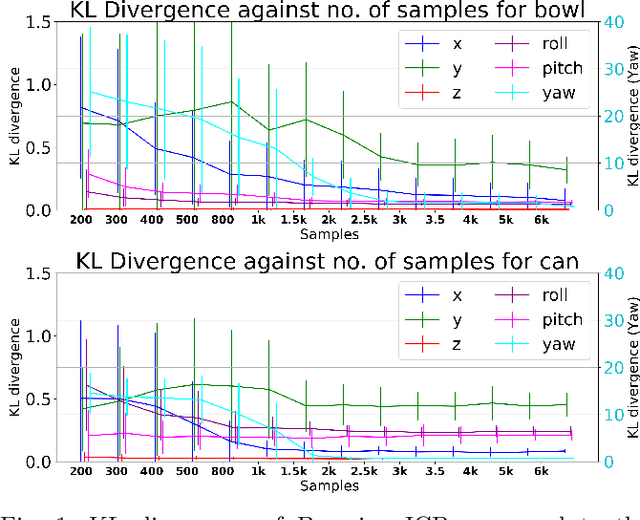
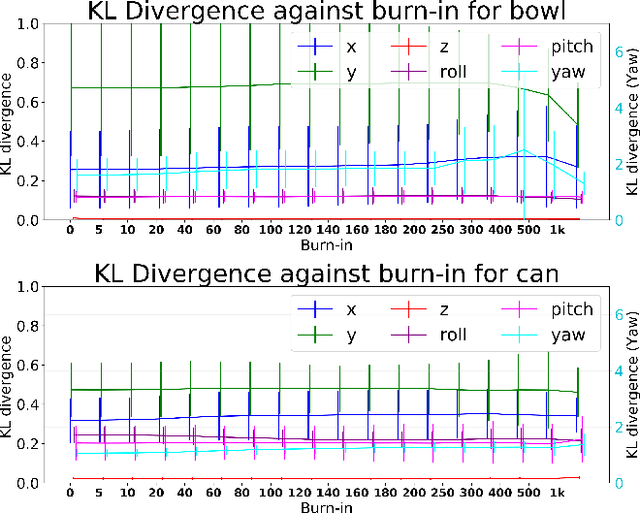
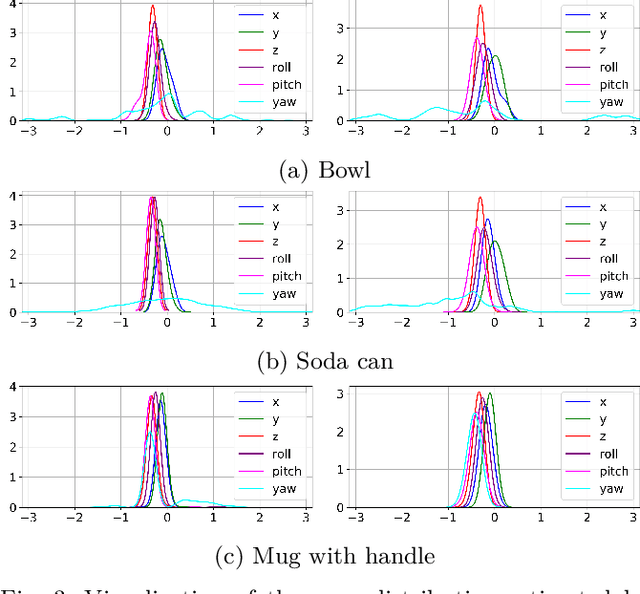

Abstract:Accurate uncertainty estimation associated with the pose transformation between two 3D point clouds is critical for autonomous navigation, grasping, and data fusion. Iterative closest point (ICP) is widely used to estimate the transformation between point cloud pairs by iteratively performing data association and motion estimation. Despite its success and popularity, ICP is effectively a deterministic algorithm, and attempts to reformulate it in a probabilistic manner generally do not capture all sources of uncertainty, such as data association errors and sensor noise. This leads to overconfident transformation estimates, potentially compromising the robustness of systems relying on them. In this paper we propose a novel method to estimate pose uncertainty in ICP with a Markov Chain Monte Carlo (MCMC) algorithm. Our method combines recent developments in optimization for scalable Bayesian sampling such as stochastic gradient Langevin dynamics (SGLD) to infer a full posterior distribution of the pose transformation between two point clouds. We evaluate our method, called Bayesian ICP, in experiments using 3D Kinect data demonstrating that our method is capable of both quickly and accuractely estimating pose uncertainty, taking into account data association uncertainty as reflected by the shape of the objects.
Speeding Up Iterative Closest Point Using Stochastic Gradient Descent
Jul 22, 2019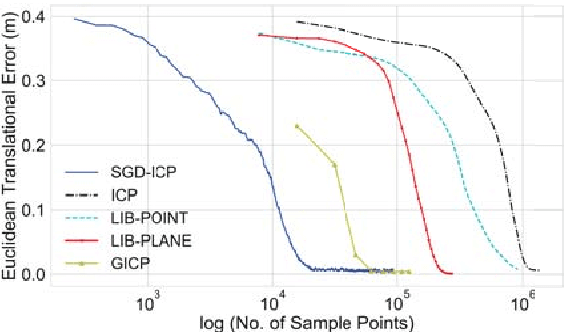
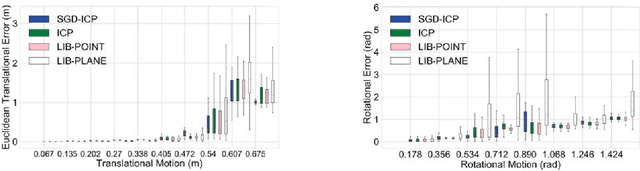

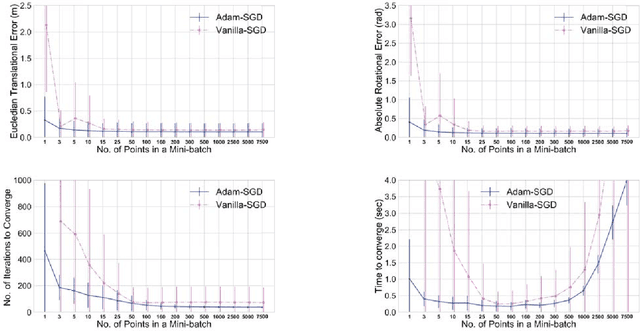
Abstract:Sensors producing 3D point clouds such as 3D laser scanners and RGB-D cameras are widely used in robotics, be it for autonomous driving or manipulation. Aligning point clouds produced by these sensors is a vital component in such applications to perform tasks such as model registration, pose estimation, and SLAM. Iterative closest point (ICP) is the most widely used method for this task, due to its simplicity and efficiency. In this paper we propose a novel method which solves the optimisation problem posed by ICP using stochastic gradient descent (SGD). Using SGD allows us to improve the convergence speed of ICP without sacrificing solution quality. Experiments using Kinect as well as Velodyne data show that, our proposed method is faster than existing methods, while obtaining solutions comparable to standard ICP. An additional benefit is robustness to parameters when processing data from different sensors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge