Estimating Motion Uncertainty with Bayesian ICP
Paper and Code
Apr 16, 2020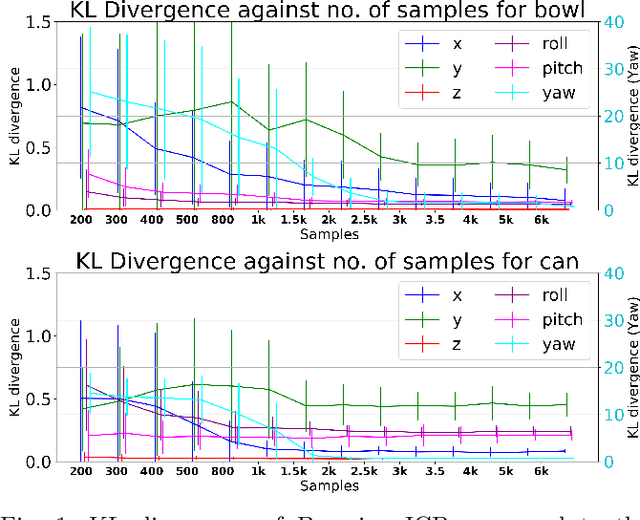
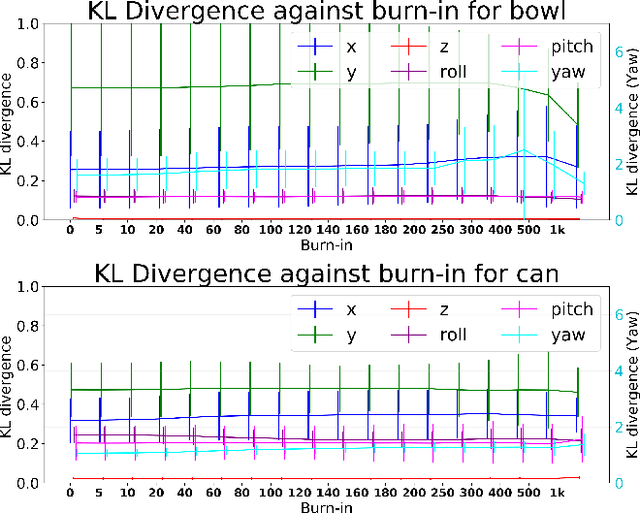
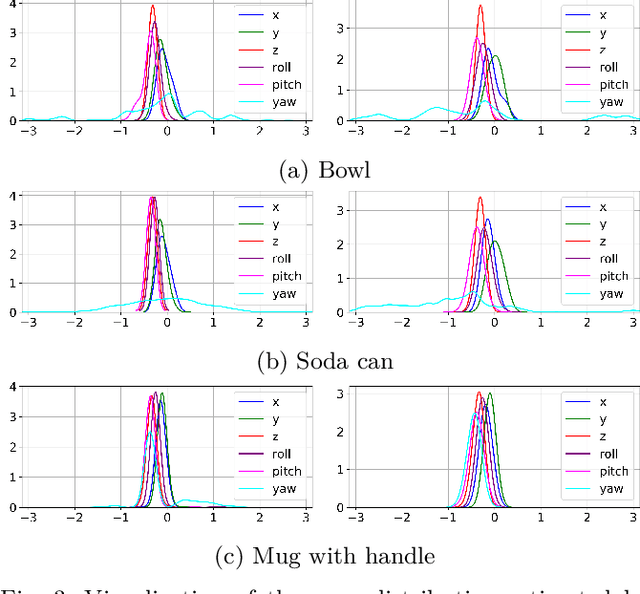

Accurate uncertainty estimation associated with the pose transformation between two 3D point clouds is critical for autonomous navigation, grasping, and data fusion. Iterative closest point (ICP) is widely used to estimate the transformation between point cloud pairs by iteratively performing data association and motion estimation. Despite its success and popularity, ICP is effectively a deterministic algorithm, and attempts to reformulate it in a probabilistic manner generally do not capture all sources of uncertainty, such as data association errors and sensor noise. This leads to overconfident transformation estimates, potentially compromising the robustness of systems relying on them. In this paper we propose a novel method to estimate pose uncertainty in ICP with a Markov Chain Monte Carlo (MCMC) algorithm. Our method combines recent developments in optimization for scalable Bayesian sampling such as stochastic gradient Langevin dynamics (SGLD) to infer a full posterior distribution of the pose transformation between two point clouds. We evaluate our method, called Bayesian ICP, in experiments using 3D Kinect data demonstrating that our method is capable of both quickly and accuractely estimating pose uncertainty, taking into account data association uncertainty as reflected by the shape of the objects.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge