HC-GAE: The Hierarchical Cluster-based Graph Auto-Encoder for Graph Representation Learning

Graph Auto-Encoders (GAEs) are powerful tools for graph representation learning. In this paper, we develop a novel Hierarchical Cluster-based GAE (HC-GAE), that can learn effective structural characteristics for graph data analysis. To this end, during the encoding process, we commence by utilizing the hard node assignment to decompose a sample graph into a family of separated subgraphs. We compress each subgraph into a coarsened node, transforming the original graph into a coarsened graph. On the other hand, during the decoding process, we adopt the soft node assignment to reconstruct the original graph structure by expanding the coarsened nodes. By hierarchically performing the above compressing procedure during the decoding process as well as the expanding procedure during the decoding process, the proposed HC-GAE can effectively extract bidirectionally hierarchical structural features of the original sample graph. Furthermore, we re-design the loss function that can integrate the information from either the encoder or the decoder. Since the associated graph convolution operation of the proposed HC-GAE is restricted in each individual separated subgraph and cannot propagate the node information between different subgraphs, the proposed HC-GAE can significantly reduce the over-smoothing problem arising in the classical convolution-based GAEs. The proposed HC-GAE can generate effective representations for either node classification or graph classification, and the experiments demonstrate the effectiveness on real-world datasets.

ENADPool: The Edge-Node Attention-based Differentiable Pooling for Graph Neural Networks

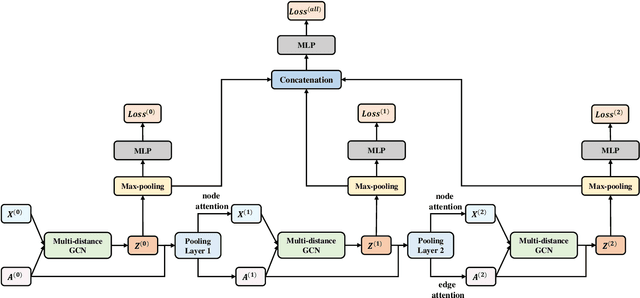
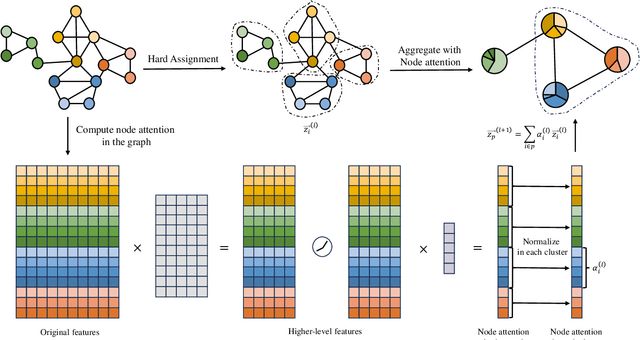
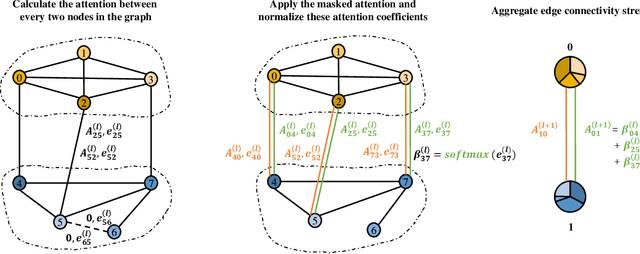
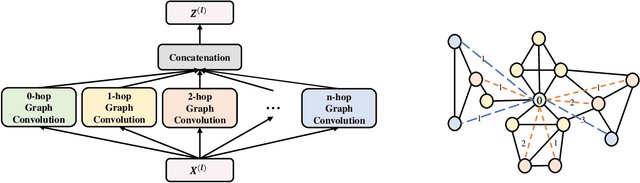
Graph Neural Networks (GNNs) are powerful tools for graph classification. One important operation for GNNs is the downsampling or pooling that can learn effective embeddings from the node representations. In this paper, we propose a new hierarchical pooling operation, namely the Edge-Node Attention-based Differentiable Pooling (ENADPool), for GNNs to learn effective graph representations. Unlike the classical hierarchical pooling operation that is based on the unclear node assignment and simply computes the averaged feature over the nodes of each cluster, the proposed ENADPool not only employs a hard clustering strategy to assign each node into an unique cluster, but also compress the node features as well as their edge connectivity strengths into the resulting hierarchical structure based on the attention mechanism after each pooling step. As a result, the proposed ENADPool simultaneously identifies the importance of different nodes within each separated cluster and edges between corresponding clusters, that significantly addresses the shortcomings of the uniform edge-node based structure information aggregation arising in the classical hierarchical pooling operation. Moreover, to mitigate the over-smoothing problem arising in existing GNNs, we propose a Multi-distance GNN (MD-GNN) model associated with the proposed ENADPool operation, allowing the nodes to actively and directly receive the feature information from neighbors at different random walk steps. Experiments demonstrate the effectiveness of the MD-GNN associated with the proposed ENADPool.

SSHPool: The Separated Subgraph-based Hierarchical Pooling

In this paper, we develop a novel local graph pooling method, namely the Separated Subgraph-based Hierarchical Pooling (SSHPool), for graph classification. To this end, we commence by assigning the nodes of a sample graph into different clusters, resulting in a family of separated subgraphs. We individually employ a local graph convolution units as the local structure to further compress each subgraph into a coarsened node, transforming the original graph into a coarsened graph. Since these subgraphs are separated by different clusters and the structural information cannot be propagated between them, the local convolution operation can significantly avoid the over-smoothing problem arising in most existing Graph Neural Networks (GNNs). By hierarchically performing the proposed procedures on the resulting coarsened graph, the proposed SSHPool can effectively extract the hierarchical global feature of the original graph structure, encapsulating rich intrinsic structural characteristics. Furthermore, we develop an end-to-end GNN framework associated with the proposed SSHPool module for graph classification. Experimental results demonstrate the superior performance of the proposed model on real-world datasets, significantly outperforming state-of-the-art GNN methods in terms of the classification accuracies.

AKBR: Learning Adaptive Kernel-based Representations for Graph Classification

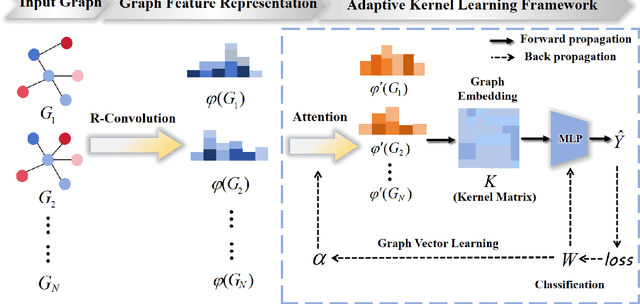
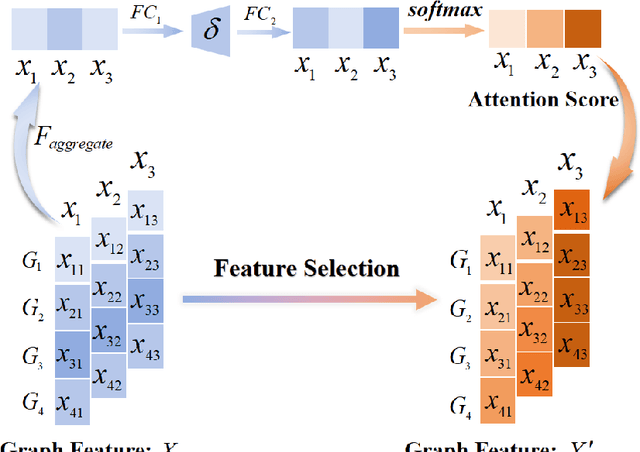
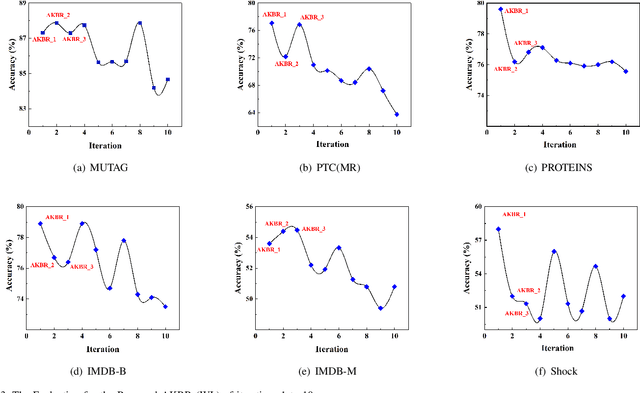
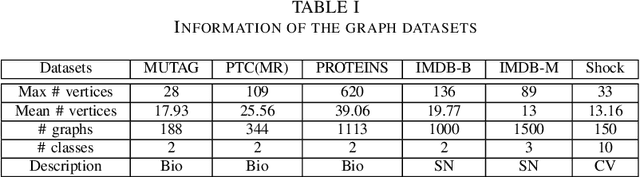
In this paper, we propose a new model to learn Adaptive Kernel-based Representations (AKBR) for graph classification. Unlike state-of-the-art R-convolution graph kernels that are defined by merely counting any pair of isomorphic substructures between graphs and cannot provide an end-to-end learning mechanism for the classifier, the proposed AKBR approach aims to define an end-to-end representation learning model to construct an adaptive kernel matrix for graphs. To this end, we commence by leveraging a novel feature-channel attention mechanism to capture the interdependencies between different substructure invariants of original graphs. The proposed AKBR model can thus effectively identify the structural importance of different substructures, and compute the R-convolution kernel between pairwise graphs associated with the more significant substructures specified by their structural attentions. Since each row of the resulting kernel matrix can be theoretically seen as the embedding vector of a sample graph, the proposed AKBR model is able to directly employ the resulting kernel matrix as the graph feature matrix and input it into the classifier for classification (i.e., the SoftMax layer), naturally providing an end-to-end learning architecture between the kernel computation as well as the classifier. Experimental results show that the proposed AKBR model outperforms existing state-of-the-art graph kernels and deep learning methods on standard graph benchmarks.

Dual-modal Prior Semantic Guided Infrared and Visible Image Fusion for Intelligent Transportation System

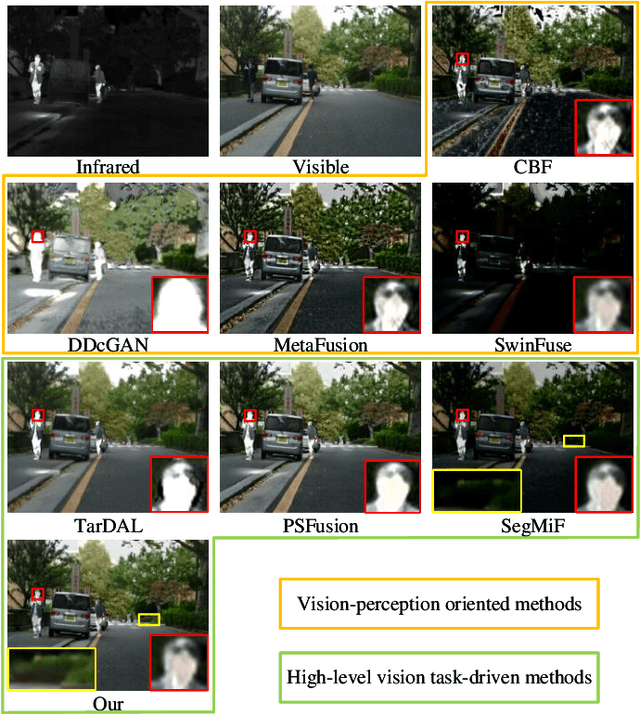
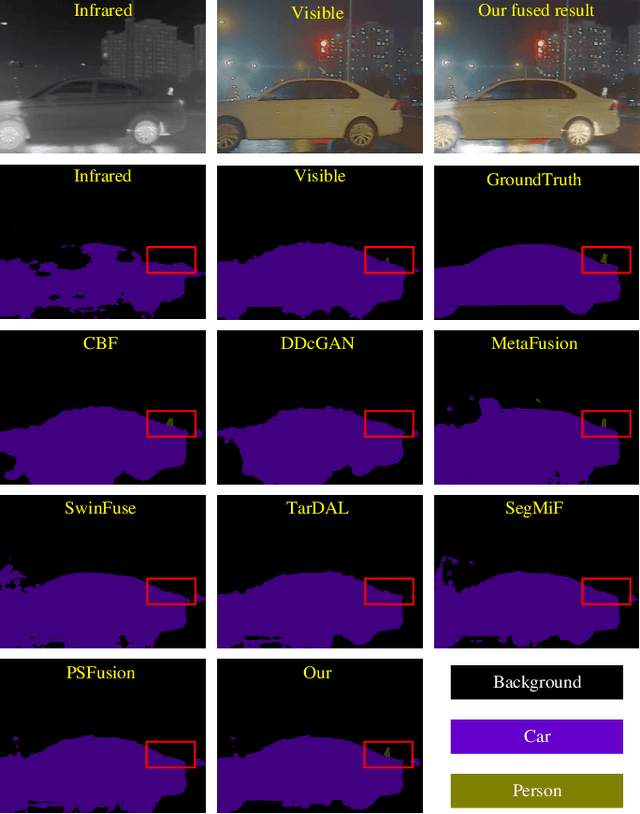
Infrared and visible image fusion (IVF) plays an important role in intelligent transportation system (ITS). The early works predominantly focus on boosting the visual appeal of the fused result, and only several recent approaches have tried to combine the high-level vision task with IVF. However, they prioritize the design of cascaded structure to seek unified suitable features and fit different tasks. Thus, they tend to typically bias toward to reconstructing raw pixels without considering the significance of semantic features. Therefore, we propose a novel prior semantic guided image fusion method based on the dual-modality strategy, improving the performance of IVF in ITS. Specifically, to explore the independent significant semantic of each modality, we first design two parallel semantic segmentation branches with a refined feature adaptive-modulation (RFaM) mechanism. RFaM can perceive the features that are semantically distinct enough in each semantic segmentation branch. Then, two pilot experiments based on the two branches are conducted to capture the significant prior semantic of two images, which then is applied to guide the fusion task in the integration of semantic segmentation branches and fusion branches. In addition, to aggregate both high-level semantics and impressive visual effects, we further investigate the frequency response of the prior semantics, and propose a multi-level representation-adaptive fusion (MRaF) module to explicitly integrate the low-frequent prior semantic with the high-frequent details. Extensive experiments on two public datasets demonstrate the superiority of our method over the state-of-the-art image fusion approaches, in terms of either the visual appeal or the high-level semantics.

Graph Representation Learning for Infrared and Visible Image Fusion

Infrared and visible image fusion aims to extract complementary features to synthesize a single fused image. Many methods employ convolutional neural networks (CNNs) to extract local features due to its translation invariance and locality. However, CNNs fail to consider the image's non-local self-similarity (NLss), though it can expand the receptive field by pooling operations, it still inevitably leads to information loss. In addition, the transformer structure extracts long-range dependence by considering the correlativity among all image patches, leading to information redundancy of such transformer-based methods. However, graph representation is more flexible than grid (CNN) or sequence (transformer structure) representation to address irregular objects, and graph can also construct the relationships among the spatially repeatable details or texture with far-space distance. Therefore, to address the above issues, it is significant to convert images into the graph space and thus adopt graph convolutional networks (GCNs) to extract NLss. This is because the graph can provide a fine structure to aggregate features and propagate information across the nearest vertices without introducing redundant information. Concretely, we implement a cascaded NLss extraction pattern to extract NLss of intra- and inter-modal by exploring interactions of different image pixels in intra- and inter-image positional distance. We commence by preforming GCNs on each intra-modal to aggregate features and propagate information to extract independent intra-modal NLss. Then, GCNs are performed on the concatenate intra-modal NLss features of infrared and visible images, which can explore the cross-domain NLss of inter-modal to reconstruct the fused image. Ablation studies and extensive experiments illustrates the effectiveness and superiority of the proposed method on three datasets.

Diffusion-Jump GNNs: Homophiliation via Learnable Metric Filters

High-order Graph Neural Networks (HO-GNNs) have been developed to infer consistent latent spaces in the heterophilic regime, where the label distribution is not correlated with the graph structure. However, most of the existing HO-GNNs are hop-based, i.e., they rely on the powers of the transition matrix. As a result, these architectures are not fully reactive to the classification loss and the achieved structural filters have static supports. In other words, neither the filters' supports nor their coefficients can be learned with these networks. They are confined, instead, to learn combinations of filters. To address the above concerns, we propose Diffusion-jump GNNs a method relying on asymptotic diffusion distances that operates on jumps. A diffusion-pump generates pairwise distances whose projections determine both the support and coefficients of each structural filter. These filters are called jumps because they explore a wide range of scales in order to find bonds between scattered nodes with the same label. Actually, the full process is controlled by the classification loss. Both the jumps and the diffusion distances react to classification errors (i.e. they are learnable). Homophiliation, i.e., the process of learning piecewise smooth latent spaces in the heterophilic regime, is formulated as a Dirichlet problem: the known labels determine the border nodes and the diffusion-pump ensures a minimal deviation of the semi-supervised grouping from a canonical unsupervised grouping. This triggers the update of both the diffusion distances and, consequently, the jumps in order to minimize the classification error. The Dirichlet formulation has several advantages. It leads to the definition of structural heterophily, a novel measure beyond edge heterophily. It also allows us to investigate links with (learnable) diffusion distances, absorbing random walks and stochastic diffusion.

AERK: Aligned Entropic Reproducing Kernels through Continuous-time Quantum Walks

In this work, we develop an Aligned Entropic Reproducing Kernel (AERK) for graph classification. We commence by performing the Continuous-time Quantum Walk (CTQW) on each graph structure, and computing the Averaged Mixing Matrix (AMM) to describe how the CTQW visit all vertices from a starting vertex. More specifically, we show how this AMM matrix allows us to compute a quantum Shannon entropy for each vertex of a graph. For pairwise graphs, the proposed AERK kernel is defined by computing a reproducing kernel based similarity between the quantum Shannon entropies of their each pair of aligned vertices. The analysis of theoretical properties reveals that the proposed AERK kernel cannot only address the shortcoming of neglecting the structural correspondence information between graphs arising in most existing R-convolution graph kernels, but also overcome the problem of neglecting the structural differences between pairs of aligned vertices arising in existing vertex-based matching kernels. Moreover, unlike existing classical graph kernels that only focus on the global or local structural information of graphs, the proposed AERK kernel can simultaneously capture both global and local structural information through the quantum Shannon entropies, reflecting more precise kernel based similarity measures between pairs of graphs. The above theoretical properties explain the effectiveness of the proposed kernel. The experimental evaluation on standard graph datasets demonstrates that the proposed AERK kernel is able to outperform state-of-the-art graph kernels for graph classification tasks.

Quantum Graph Learning: Frontiers and Outlook

Quantum theory has shown its superiority in enhancing machine learning. However, facilitating quantum theory to enhance graph learning is in its infancy. This survey investigates the current advances in quantum graph learning (QGL) from three perspectives, i.e., underlying theories, methods, and prospects. We first look at QGL and discuss the mutualism of quantum theory and graph learning, the specificity of graph-structured data, and the bottleneck of graph learning, respectively. A new taxonomy of QGL is presented, i.e., quantum computing on graphs, quantum graph representation, and quantum circuits for graph neural networks. Pitfall traps are then highlighted and explained. This survey aims to provide a brief but insightful introduction to this emerging field, along with a detailed discussion of frontiers and outlook yet to be investigated.

QESK: Quantum-based Entropic Subtree Kernels for Graph Classification

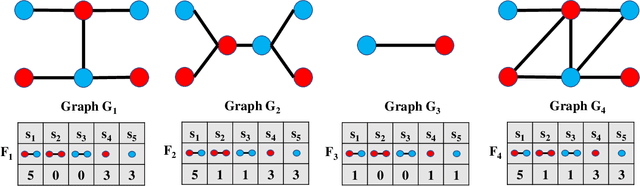
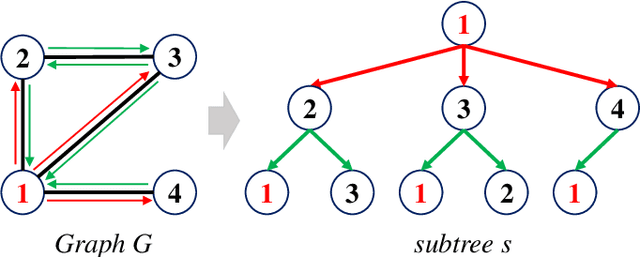
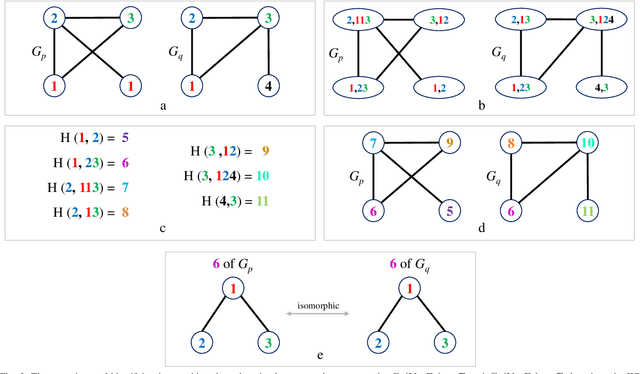
In this paper, we propose a novel graph kernel, namely the Quantum-based Entropic Subtree Kernel (QESK), for Graph Classification. To this end, we commence by computing the Average Mixing Matrix (AMM) of the Continuous-time Quantum Walk (CTQW) evolved on each graph structure. Moreover, we show how this AMM matrix can be employed to compute a series of entropic subtree representations associated with the classical Weisfeiler-Lehman (WL) algorithm. For a pair of graphs, the QESK kernel is defined by computing the exponentiation of the negative Euclidean distance between their entropic subtree representations, theoretically resulting in a positive definite graph kernel. We show that the proposed QESK kernel not only encapsulates complicated intrinsic quantum-based structural characteristics of graph structures through the CTQW, but also theoretically addresses the shortcoming of ignoring the effects of unshared substructures arising in state-of-the-art R-convolution graph kernels. Moreover, unlike the classical R-convolution kernels, the proposed QESK can discriminate the distinctions of isomorphic subtrees in terms of the global graph structures, theoretically explaining the effectiveness. Experiments indicate that the proposed QESK kernel can significantly outperform state-of-the-art graph kernels and graph deep learning methods for graph classification problems.