ENADPool: The Edge-Node Attention-based Differentiable Pooling for Graph Neural Networks
Paper and Code
May 16, 2024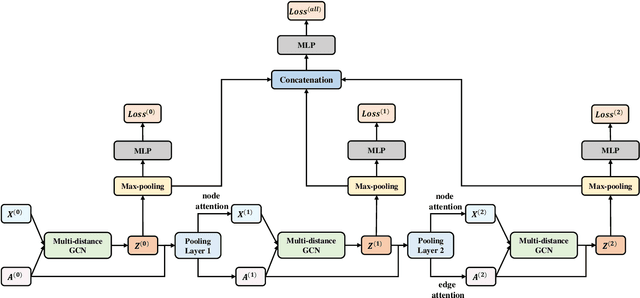
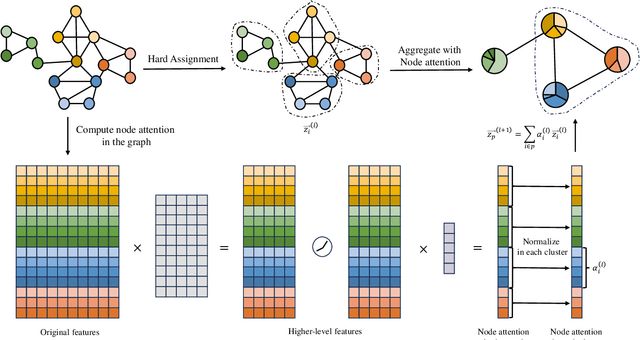
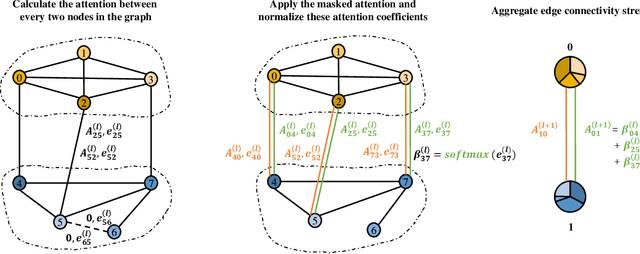
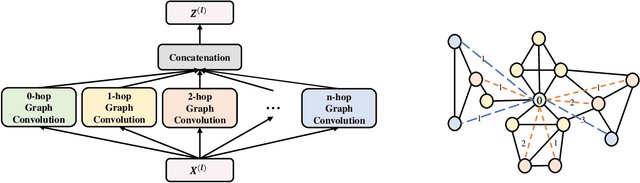
Graph Neural Networks (GNNs) are powerful tools for graph classification. One important operation for GNNs is the downsampling or pooling that can learn effective embeddings from the node representations. In this paper, we propose a new hierarchical pooling operation, namely the Edge-Node Attention-based Differentiable Pooling (ENADPool), for GNNs to learn effective graph representations. Unlike the classical hierarchical pooling operation that is based on the unclear node assignment and simply computes the averaged feature over the nodes of each cluster, the proposed ENADPool not only employs a hard clustering strategy to assign each node into an unique cluster, but also compress the node features as well as their edge connectivity strengths into the resulting hierarchical structure based on the attention mechanism after each pooling step. As a result, the proposed ENADPool simultaneously identifies the importance of different nodes within each separated cluster and edges between corresponding clusters, that significantly addresses the shortcomings of the uniform edge-node based structure information aggregation arising in the classical hierarchical pooling operation. Moreover, to mitigate the over-smoothing problem arising in existing GNNs, we propose a Multi-distance GNN (MD-GNN) model associated with the proposed ENADPool operation, allowing the nodes to actively and directly receive the feature information from neighbors at different random walk steps. Experiments demonstrate the effectiveness of the MD-GNN associated with the proposed ENADPool.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge