Diffusion-Jump GNNs: Homophiliation via Learnable Metric Filters

High-order Graph Neural Networks (HO-GNNs) have been developed to infer consistent latent spaces in the heterophilic regime, where the label distribution is not correlated with the graph structure. However, most of the existing HO-GNNs are hop-based, i.e., they rely on the powers of the transition matrix. As a result, these architectures are not fully reactive to the classification loss and the achieved structural filters have static supports. In other words, neither the filters' supports nor their coefficients can be learned with these networks. They are confined, instead, to learn combinations of filters. To address the above concerns, we propose Diffusion-jump GNNs a method relying on asymptotic diffusion distances that operates on jumps. A diffusion-pump generates pairwise distances whose projections determine both the support and coefficients of each structural filter. These filters are called jumps because they explore a wide range of scales in order to find bonds between scattered nodes with the same label. Actually, the full process is controlled by the classification loss. Both the jumps and the diffusion distances react to classification errors (i.e. they are learnable). Homophiliation, i.e., the process of learning piecewise smooth latent spaces in the heterophilic regime, is formulated as a Dirichlet problem: the known labels determine the border nodes and the diffusion-pump ensures a minimal deviation of the semi-supervised grouping from a canonical unsupervised grouping. This triggers the update of both the diffusion distances and, consequently, the jumps in order to minimize the classification error. The Dirichlet formulation has several advantages. It leads to the definition of structural heterophily, a novel measure beyond edge heterophily. It also allows us to investigate links with (learnable) diffusion distances, absorbing random walks and stochastic diffusion.

DiffWire: Inductive Graph Rewiring via the Lovász Bound

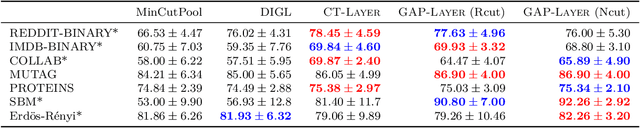
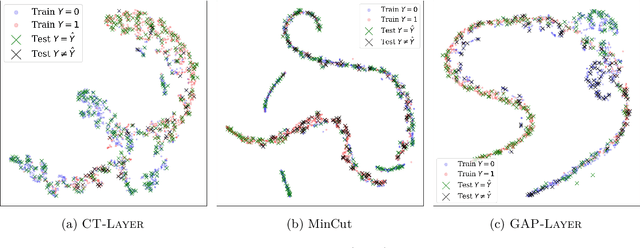
Graph Neural Networks (GNNs) have been shown to achieve competitive results to tackle graph-related tasks, such as node and graph classification, link prediction and node and graph clustering in a variety of domains. Most GNNs use a message passing framework and hence are called MPNNs. Despite their promising results, MPNNs have been reported to suffer from over-smoothing, over-squashing and under-reaching. Graph rewiring and graph pooling have been proposed in the literature as solutions to address these limitations. However, most state-of-the-art graph rewiring methods fail to preserve the global topology of the graph, are not differentiable (inductive) and require the tuning of hyper-parameters. In this paper, we propose DiffWire, a novel framework for graph rewiring in MPNNs that is principled, fully differentiable and parameter-free by leveraging the Lov\'asz bound. Our approach provides a unified theory for graph rewiring by proposing two new, complementary layers in MPNNs: first, CTLayer, a layer that learns the commute times and uses them as a relevance function for edge re-weighting; second, GAPLayer, a layer to optimize the spectral gap, depending on the nature of the network and the task at hand. We empirically validate the value of our proposed approach and each of these layers separately with benchmark datasets for graph classification. DiffWire brings together the learnability of commute times to related definitions of curvature, opening the door to the development of more expressive MPNNs.