LGAN: An Efficient High-Order Graph Neural Network via the Line Graph Aggregation

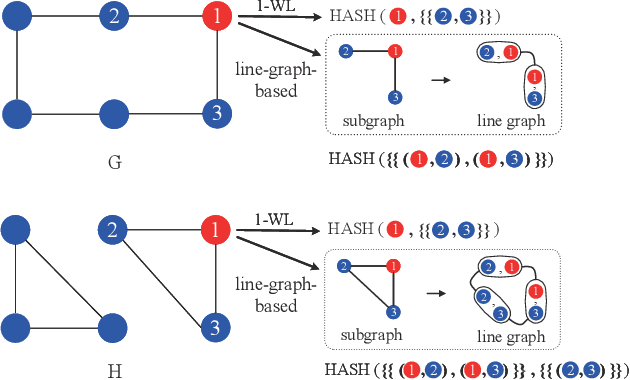
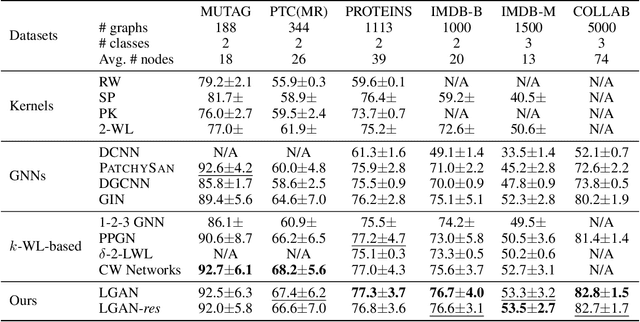
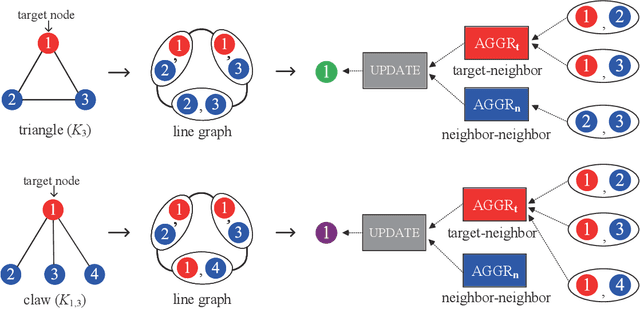
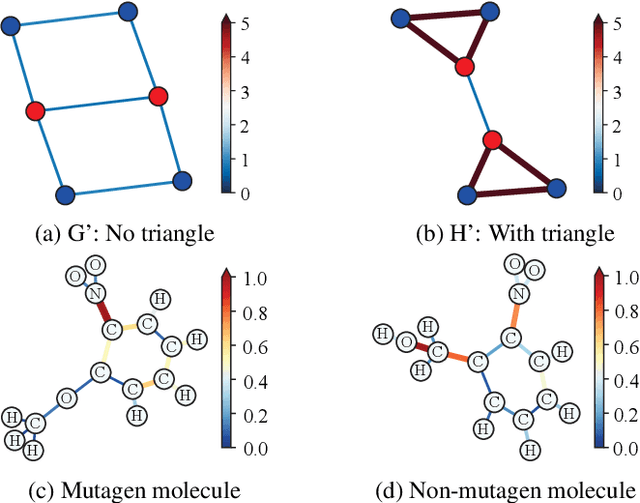
Graph Neural Networks (GNNs) have emerged as a dominant paradigm for graph classification. Specifically, most existing GNNs mainly rely on the message passing strategy between neighbor nodes, where the expressivity is limited by the 1-dimensional Weisfeiler-Lehman (1-WL) test. Although a number of k-WL-based GNNs have been proposed to overcome this limitation, their computational cost increases rapidly with k, significantly restricting the practical applicability. Moreover, since the k-WL models mainly operate on node tuples, these k-WL-based GNNs cannot retain fine-grained node- or edge-level semantics required by attribution methods (e.g., Integrated Gradients), leading to the less interpretable problem. To overcome the above shortcomings, in this paper, we propose a novel Line Graph Aggregation Network (LGAN), that constructs a line graph from the induced subgraph centered at each node to perform the higher-order aggregation. We theoretically prove that the LGAN not only possesses the greater expressive power than the 2-WL under injective aggregation assumptions, but also has lower time complexity. Empirical evaluations on benchmarks demonstrate that the LGAN outperforms state-of-the-art k-WL-based GNNs, while offering better interpretability.

SSHPool: The Separated Subgraph-based Hierarchical Pooling

In this paper, we develop a novel local graph pooling method, namely the Separated Subgraph-based Hierarchical Pooling (SSHPool), for graph classification. To this end, we commence by assigning the nodes of a sample graph into different clusters, resulting in a family of separated subgraphs. We individually employ a local graph convolution units as the local structure to further compress each subgraph into a coarsened node, transforming the original graph into a coarsened graph. Since these subgraphs are separated by different clusters and the structural information cannot be propagated between them, the local convolution operation can significantly avoid the over-smoothing problem arising in most existing Graph Neural Networks (GNNs). By hierarchically performing the proposed procedures on the resulting coarsened graph, the proposed SSHPool can effectively extract the hierarchical global feature of the original graph structure, encapsulating rich intrinsic structural characteristics. Furthermore, we develop an end-to-end GNN framework associated with the proposed SSHPool module for graph classification. Experimental results demonstrate the superior performance of the proposed model on real-world datasets, significantly outperforming state-of-the-art GNN methods in terms of the classification accuracies.

AKBR: Learning Adaptive Kernel-based Representations for Graph Classification

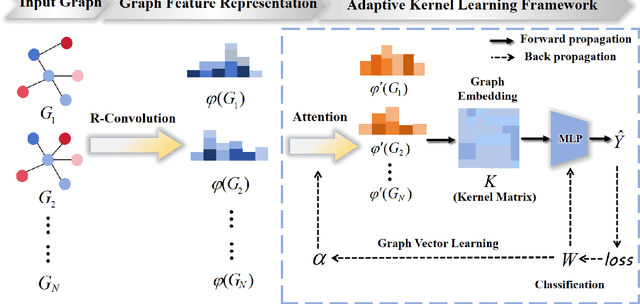
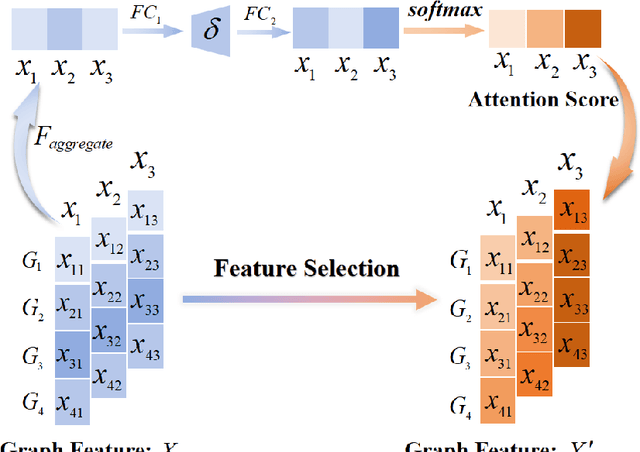
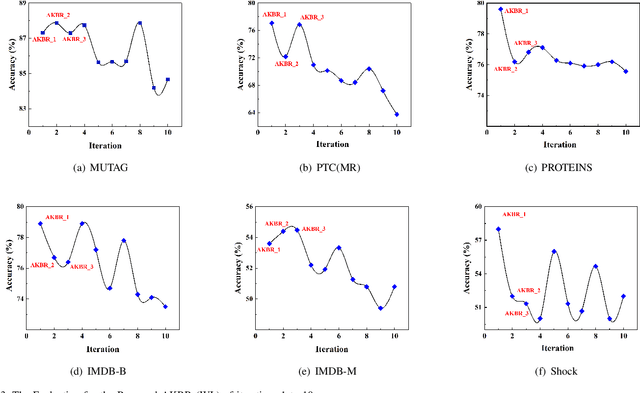
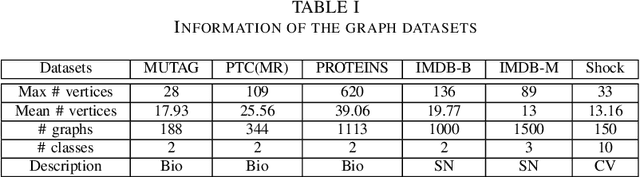
In this paper, we propose a new model to learn Adaptive Kernel-based Representations (AKBR) for graph classification. Unlike state-of-the-art R-convolution graph kernels that are defined by merely counting any pair of isomorphic substructures between graphs and cannot provide an end-to-end learning mechanism for the classifier, the proposed AKBR approach aims to define an end-to-end representation learning model to construct an adaptive kernel matrix for graphs. To this end, we commence by leveraging a novel feature-channel attention mechanism to capture the interdependencies between different substructure invariants of original graphs. The proposed AKBR model can thus effectively identify the structural importance of different substructures, and compute the R-convolution kernel between pairwise graphs associated with the more significant substructures specified by their structural attentions. Since each row of the resulting kernel matrix can be theoretically seen as the embedding vector of a sample graph, the proposed AKBR model is able to directly employ the resulting kernel matrix as the graph feature matrix and input it into the classifier for classification (i.e., the SoftMax layer), naturally providing an end-to-end learning architecture between the kernel computation as well as the classifier. Experimental results show that the proposed AKBR model outperforms existing state-of-the-art graph kernels and deep learning methods on standard graph benchmarks.