Comprehensive analysis of gene expression profiles to radiation exposure reveals molecular signatures of low-dose radiation response

There are various sources of ionizing radiation exposure, where medical exposure for radiation therapy or diagnosis is the most common human-made source. Understanding how gene expression is modulated after ionizing radiation exposure and investigating the presence of any dose-dependent gene expression patterns have broad implications for health risks from radiotherapy, medical radiation diagnostic procedures, as well as other environmental exposure. In this paper, we perform a comprehensive pathway-based analysis of gene expression profiles in response to low-dose radiation exposure, in order to examine the potential mechanism of gene regulation underlying such responses. To accomplish this goal, we employ a statistical framework to determine whether a specific group of genes belonging to a known pathway display coordinated expression patterns that are modulated in a manner consistent with the radiation level. Findings in our study suggest that there exist complex yet consistent signatures that reflect the molecular response to radiation exposure, which differ between low-dose and high-dose radiation.

Adaptive Group Testing with Mismatched Models

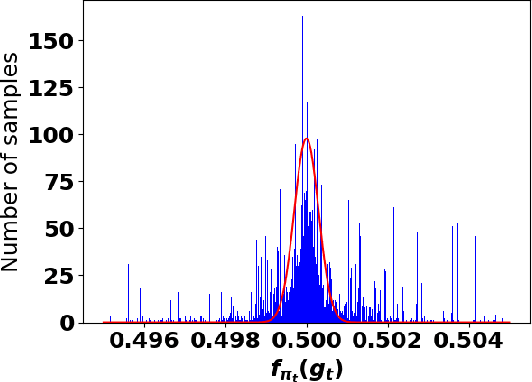
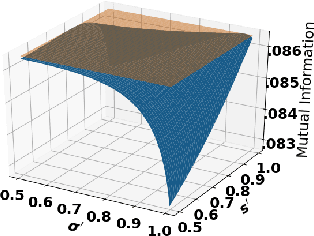
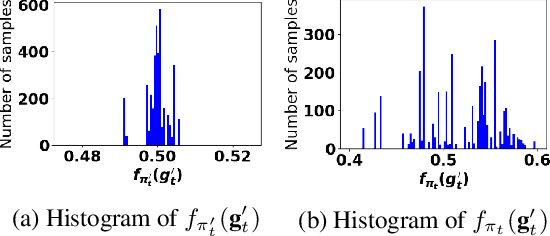
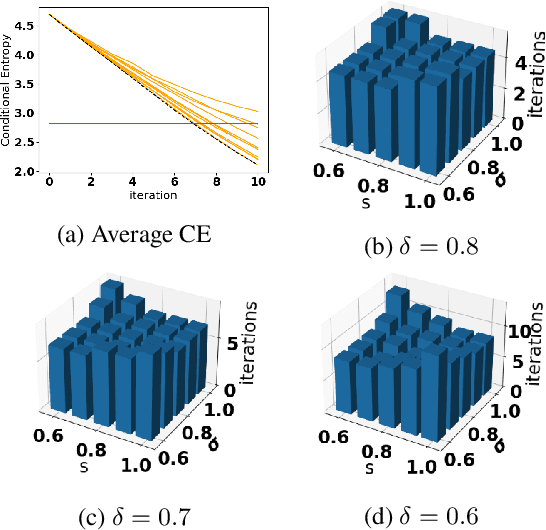
Accurate detection of infected individuals is one of the critical steps in stopping any pandemic. When the underlying infection rate of the disease is low, testing people in groups, instead of testing each individual in the population, can be more efficient. In this work, we consider noisy adaptive group testing design with specific test sensitivity and specificity that select the optimal group given previous test results based on pre-selected utility function. As in prior studies on group testing, we model this problem as a sequential Bayesian Optimal Experimental Design (BOED) to adaptively design the groups for each test. We analyze the required number of group tests when using the updated posterior on the infection status and the corresponding Mutual Information (MI) as our utility function for selecting new groups. More importantly, we study how the potential bias on the ground-truth noise of group tests may affect the group testing sample complexity.

Optimal Decision Making in High-Throughput Virtual Screening Pipelines

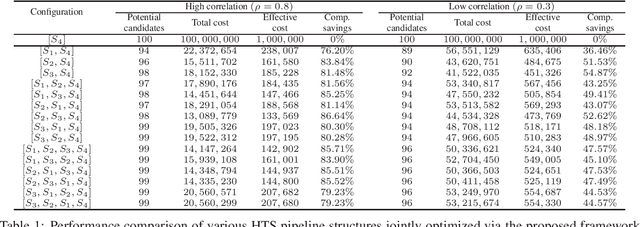
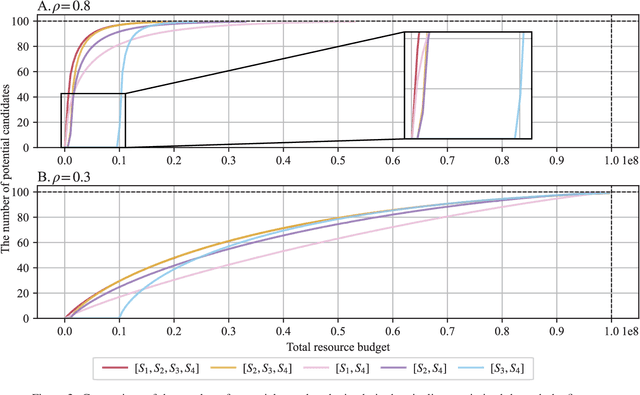
Effective selection of the potential candidates that meet certain conditions in a tremendously large search space has been one of the major concerns in many real-world applications. In addition to the nearly infinitely large search space, rigorous evaluation of a sample based on the reliable experimental or computational platform is often prohibitively expensive, making the screening problem more challenging. In such a case, constructing a high-throughput screening (HTS) pipeline that pre-sifts the samples expected to be potential candidates through the efficient earlier stages, results in a significant amount of savings in resources. However, to the best of our knowledge, despite many successful applications, no one has studied optimal pipeline design or optimal pipeline operations. In this study, we propose two optimization frameworks, applying to most (if not all) screening campaigns involving experimental or/and computational evaluations, for optimally determining the screening thresholds of an HTS pipeline. We validate the proposed frameworks on both analytic and practical scenarios. In particular, we consider the optimal computational campaign for the long non-coding RNA (lncRNA) classification as a practical example. To accomplish this, we built the high-throughput virtual screening (HTVS) pipeline for classifying the lncRNA. The simulation results demonstrate that the proposed frameworks significantly reduce the effective selection cost per potential candidate and make the HTS pipelines less sensitive to their structural variations. In addition to the validation, we provide insights on constructing a better HTS pipeline based on the simulation results.

Robust Importance Sampling for Error Estimation in the Context of Optimal Bayesian Transfer Learning

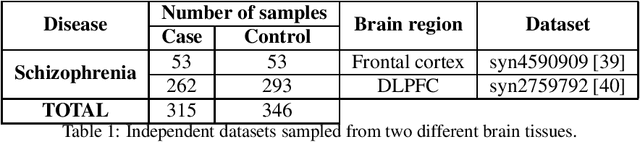
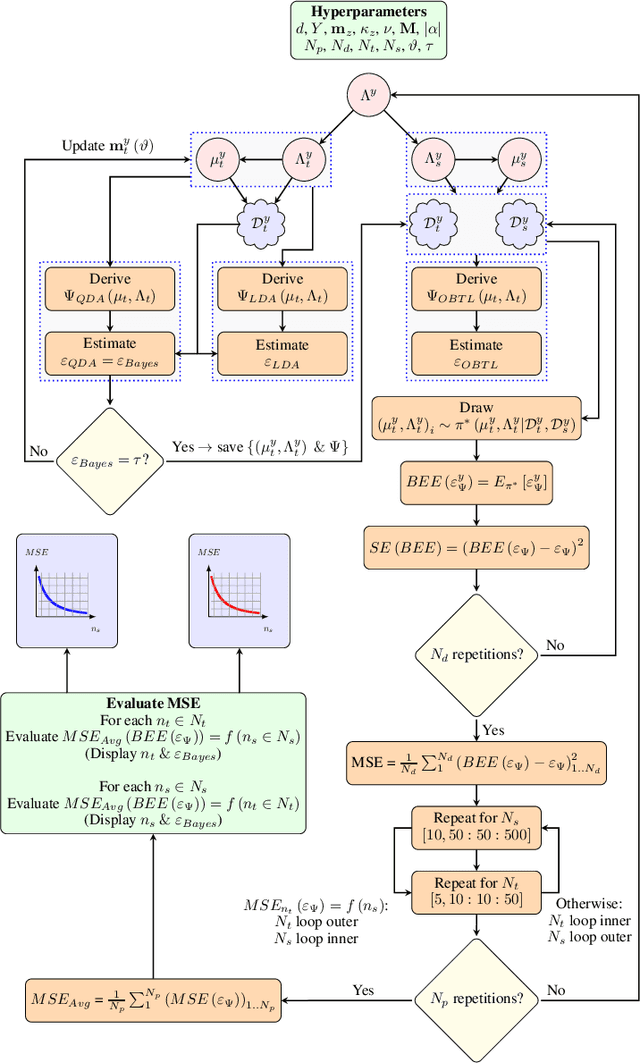
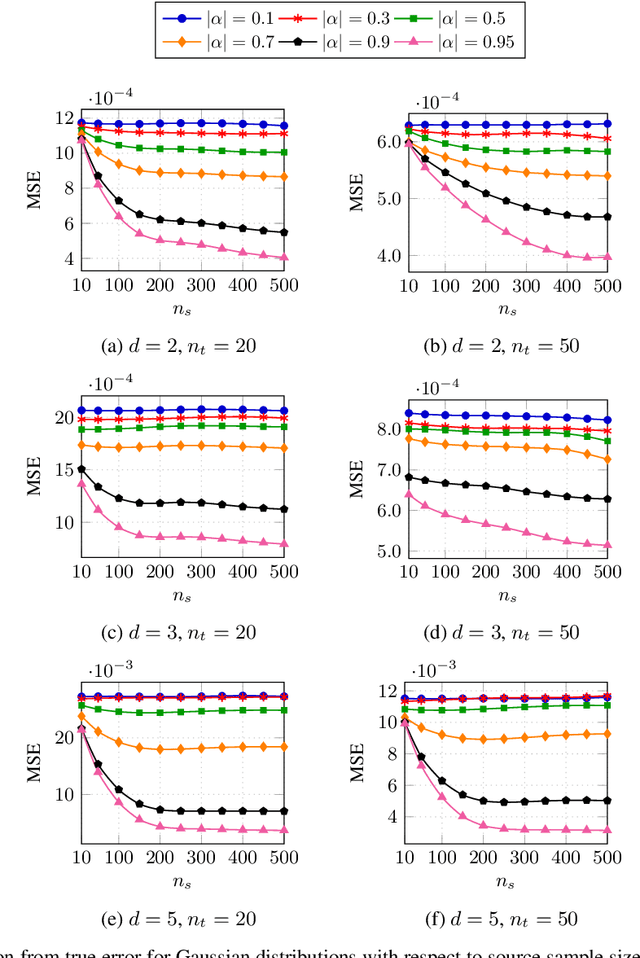
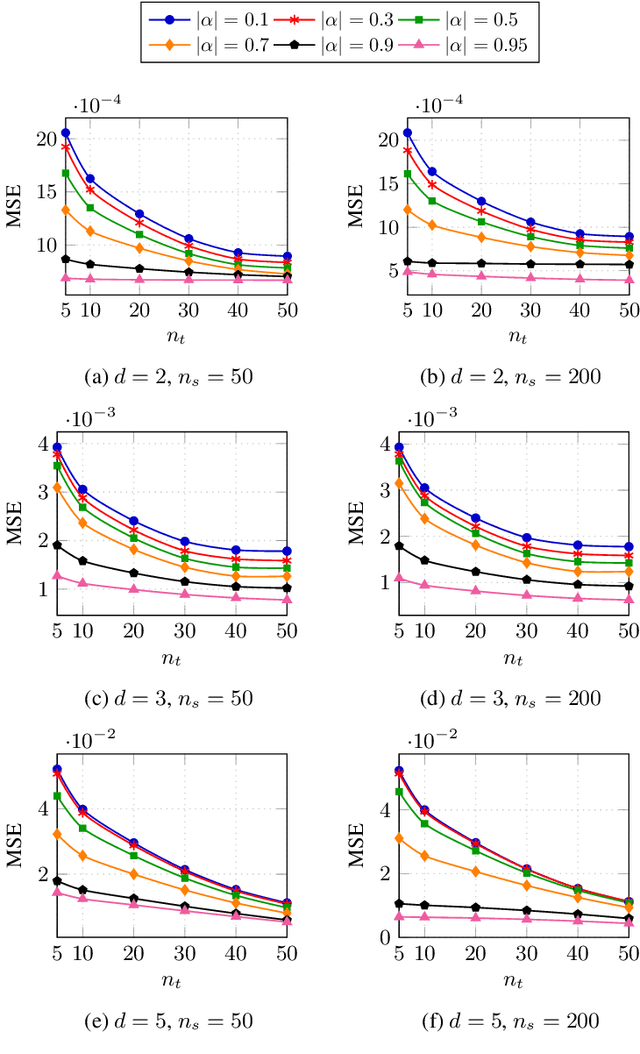
Classification has been a major task for building intelligent systems as it enables decision-making under uncertainty. Classifier design aims at building models from training data for representing feature-label distributions--either explicitly or implicitly. In many scientific or clinical settings, training data are typically limited, which makes designing accurate classifiers and evaluating their classification error extremely challenging. While transfer learning (TL) can alleviate this issue by incorporating data from relevant source domains to improve learning in a different target domain, it has received little attention for performance assessment, notably in error estimation. In this paper, we fill this gap by investigating knowledge transferability in the context of classification error estimation within a Bayesian paradigm. We introduce a novel class of Bayesian minimum mean-square error (MMSE) estimators for optimal Bayesian transfer learning (OBTL), which enables rigorous evaluation of classification error under uncertainty in a small-sample setting. Using Monte Carlo importance sampling, we employ the proposed estimator to evaluate the classification accuracy of a broad family of classifiers that span diverse learning capabilities. Experimental results based on both synthetic data as well as real-world RNA sequencing (RNA-seq) data show that our proposed OBTL error estimation scheme clearly outperforms standard error estimators, especially in a small-sample setting, by tapping into the data from other relevant domains.

Quantifying the multi-objective cost of uncertainty

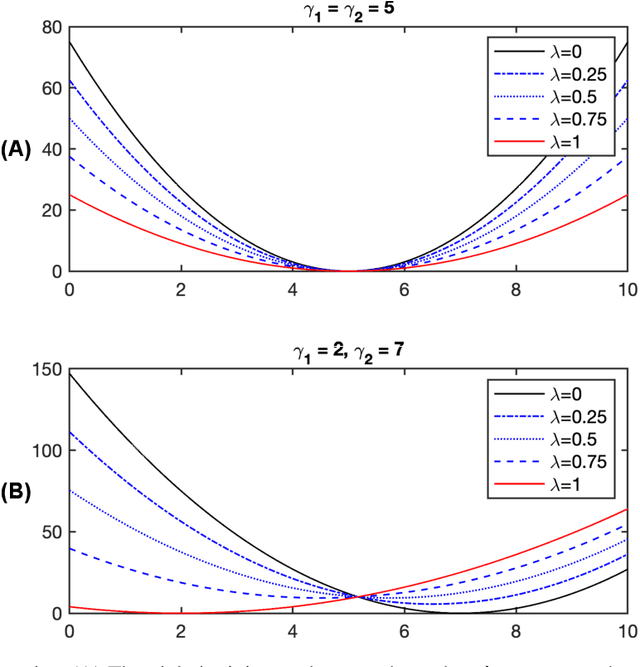
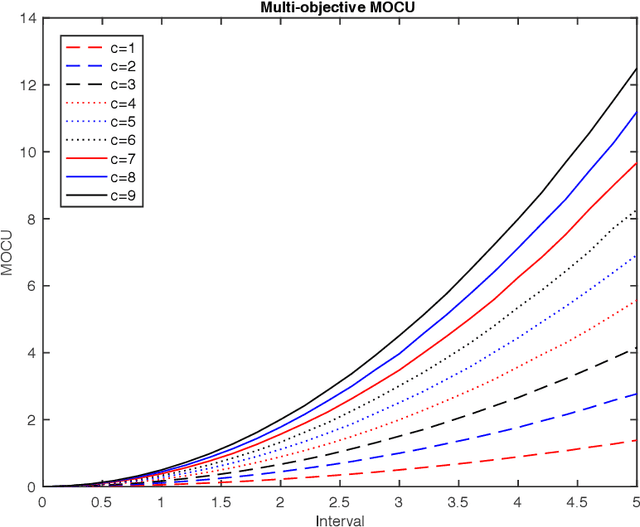
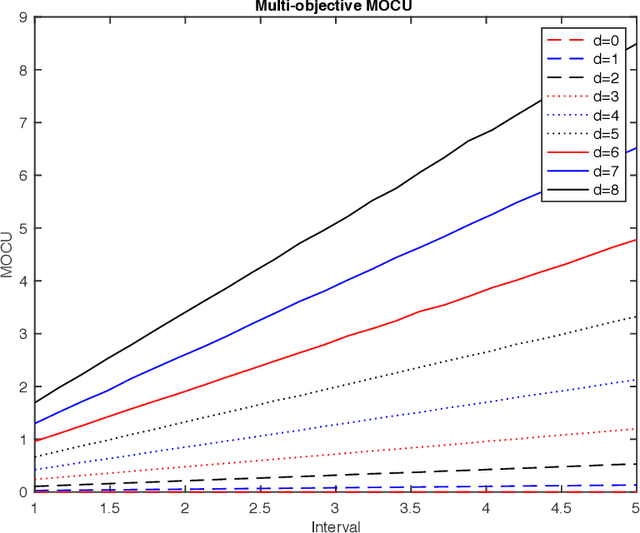
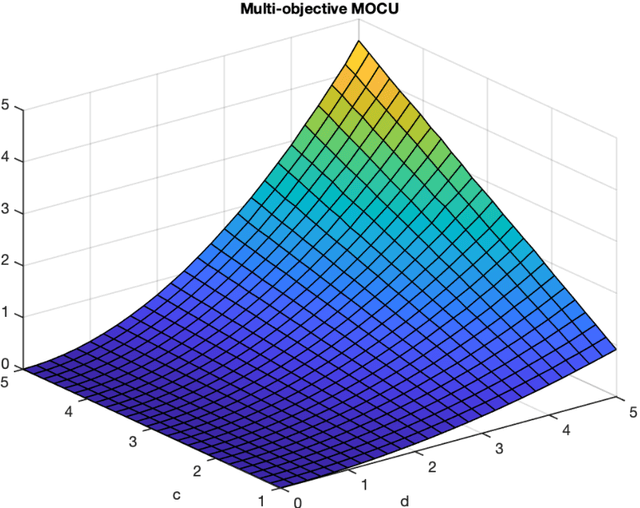
Various real-world applications involve modeling complex systems with immense uncertainty and optimizing multiple objectives based on the uncertain model. Quantifying the impact of the model uncertainty on the given operational objectives is critical for designing optimal experiments that can most effectively reduce the uncertainty that affect the objectives pertinent to the application at hand. In this paper, we propose the concept of mean multi-objective cost of uncertainty (multi-objective MOCU) that can be used for objective-based quantification of uncertainty for complex uncertain systems considering multiple operational objectives. We provide several illustrative examples that demonstrate the concept and strengths of the proposed multi-objective MOCU.

Optimal Clustering with Missing Values

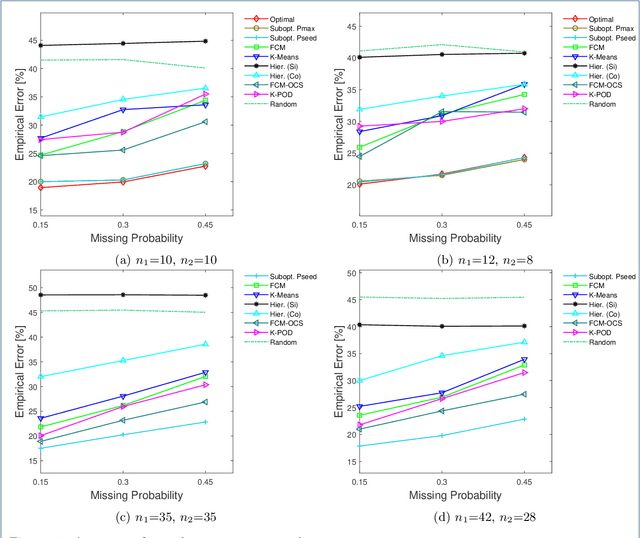
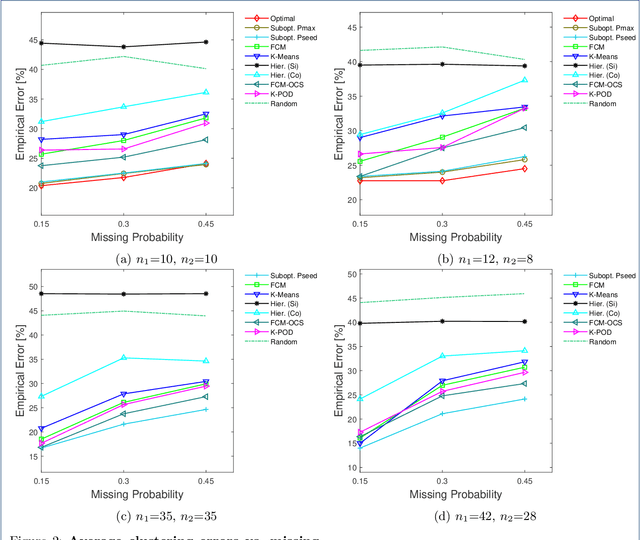
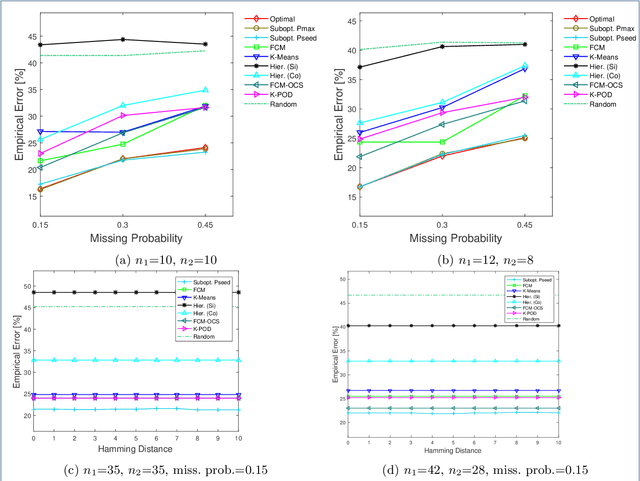
Missing values frequently arise in modern biomedical studies due to various reasons, including missing tests or complex profiling technologies for different omics measurements. Missing values can complicate the application of clustering algorithms, whose goals are to group points based on some similarity criterion. A common practice for dealing with missing values in the context of clustering is to first impute the missing values, and then apply the clustering algorithm on the completed data. We consider missing values in the context of optimal clustering, which finds an optimal clustering operator with reference to an underlying random labeled point process (RLPP). We show how the missing-value problem fits neatly into the overall framework of optimal clustering by incorporating the missing value mechanism into the random labeled point process and then marginalizing out the missing-value process. In particular, we demonstrate the proposed framework for the Gaussian model with arbitrary covariance structures. Comprehensive experimental studies on both synthetic and real-world RNA-seq data show the superior performance of the proposed optimal clustering with missing values when compared to various clustering approaches. Optimal clustering with missing values obviates the need for imputation-based pre-processing of the data, while at the same time possessing smaller clustering errors.

Optimal Clustering under Uncertainty

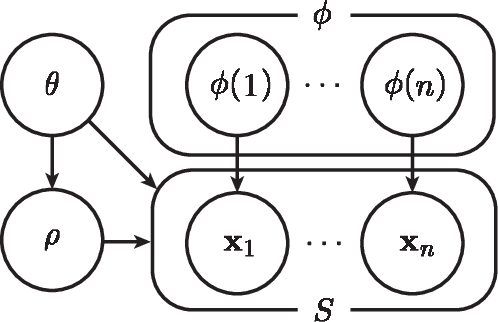
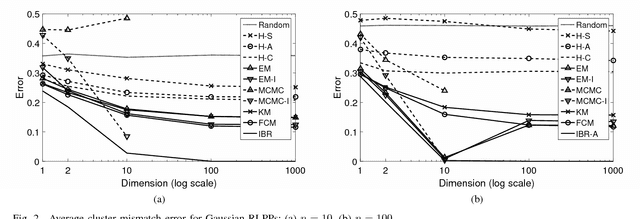
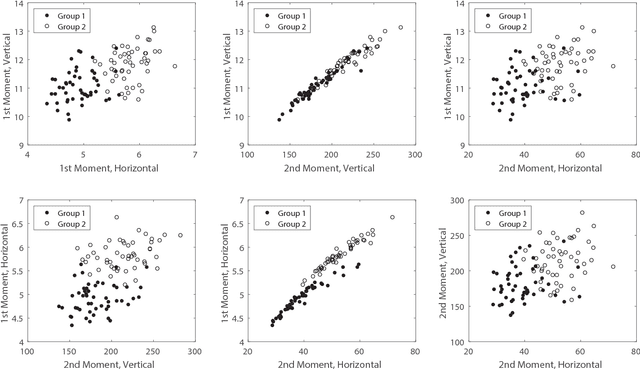
Classical clustering algorithms typically either lack an underlying probability framework to make them predictive or focus on parameter estimation rather than defining and minimizing a notion of error. Recent work addresses these issues by developing a probabilistic framework based on the theory of random labeled point processes and characterizing a Bayes clusterer that minimizes the number of misclustered points. The Bayes clusterer is analogous to the Bayes classifier. Whereas determining a Bayes classifier requires full knowledge of the feature-label distribution, deriving a Bayes clusterer requires full knowledge of the point process. When uncertain of the point process, one would like to find a robust clusterer that is optimal over the uncertainty, just as one may find optimal robust classifiers with uncertain feature-label distributions. Herein, we derive an optimal robust clusterer by first finding an effective random point process that incorporates all randomness within its own probabilistic structure and from which a Bayes clusterer can be derived that provides an optimal robust clusterer relative to the uncertainty. This is analogous to the use of effective class-conditional distributions in robust classification. After evaluating the performance of robust clusterers in synthetic mixtures of Gaussians models, we apply the framework to granular imaging, where we make use of the asymptotic granulometric moment theory for granular images to relate robust clustering theory to the application.

Optimal Bayesian Transfer Learning

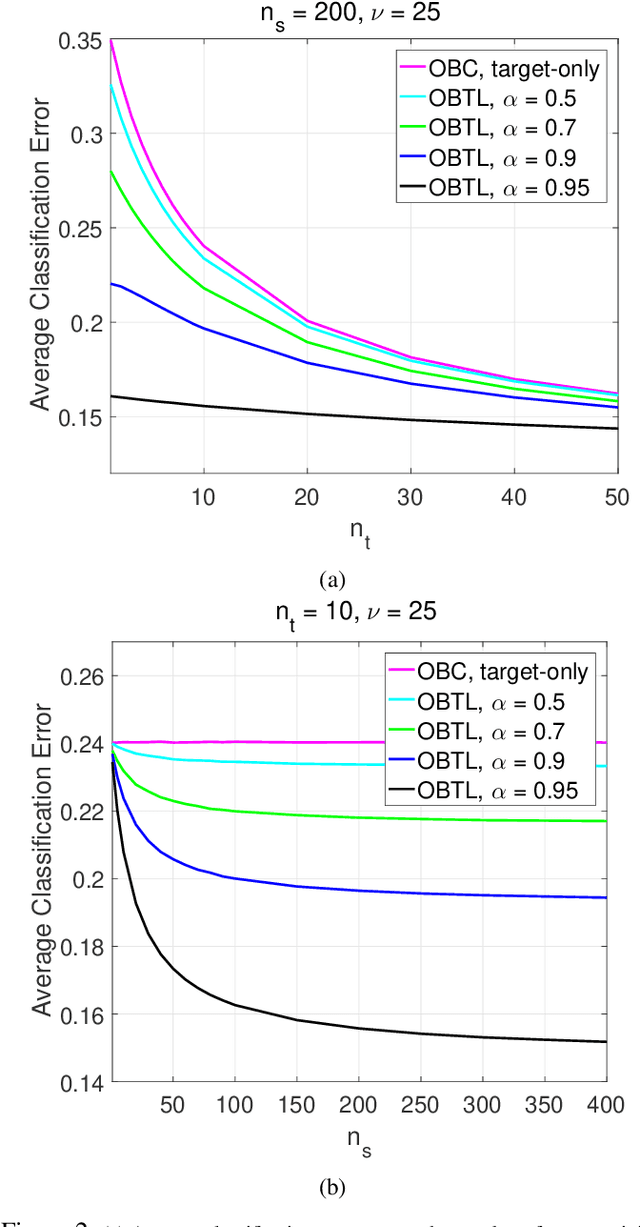
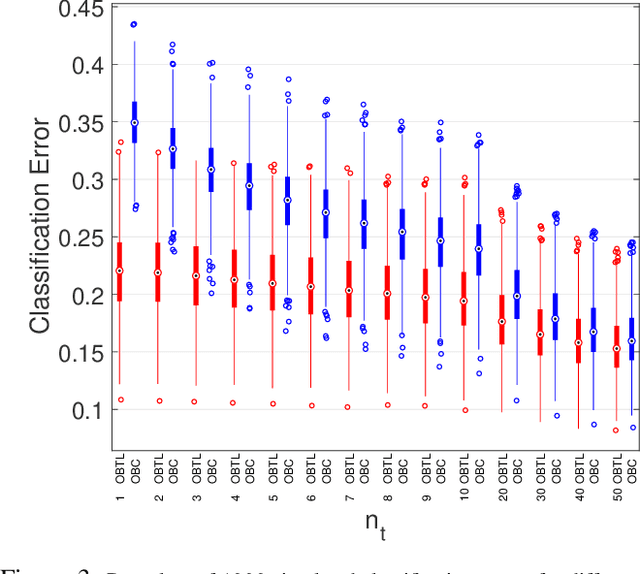
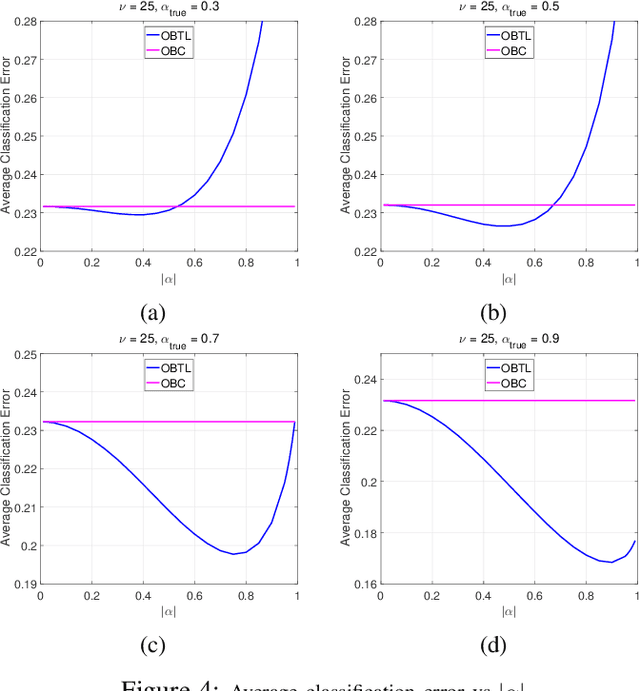
Transfer learning has recently attracted significant research attention, as it simultaneously learns from different source domains, which have plenty of labeled data, and transfers the relevant knowledge to the target domain with limited labeled data to improve the prediction performance. We propose a Bayesian transfer learning framework where the source and target domains are related through the joint prior density of the model parameters. The modeling of joint prior densities enables better understanding of the "transferability" between domains. We define a joint Wishart density for the precision matrices of the Gaussian feature-label distributions in the source and target domains to act like a bridge that transfers the useful information of the source domain to help classification in the target domain by improving the target posteriors. Using several theorems in multivariate statistics, the posteriors and posterior predictive densities are derived in closed forms with hypergeometric functions of matrix argument, leading to our novel closed-form and fast Optimal Bayesian Transfer Learning (OBTL) classifier. Experimental results on both synthetic and real-world benchmark data confirm the superb performance of the OBTL compared to the other state-of-the-art transfer learning and domain adaptation methods.

Moments and Root-Mean-Square Error of the Bayesian MMSE Estimator of Classification Error in the Gaussian Model

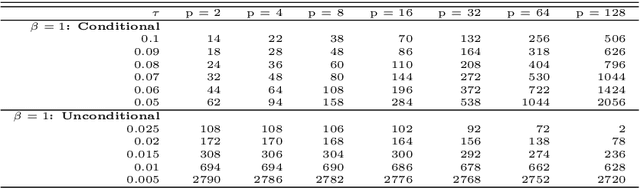
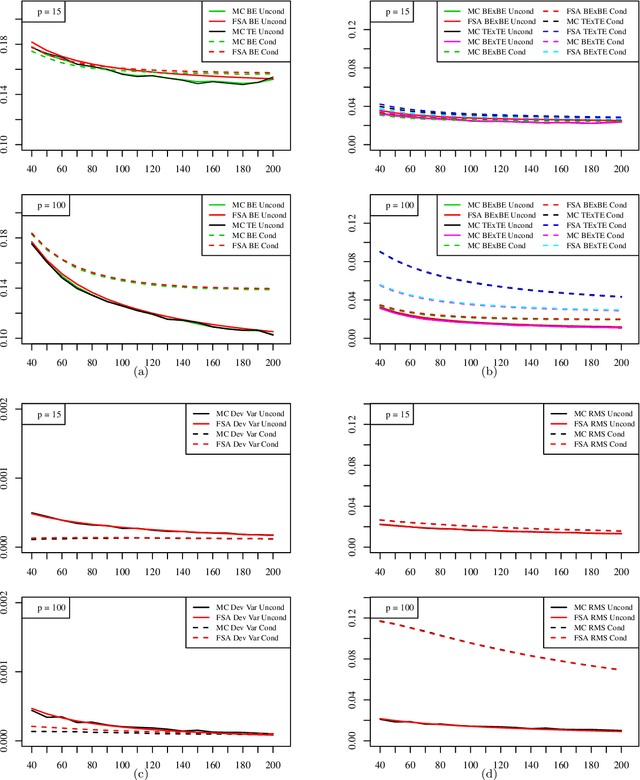
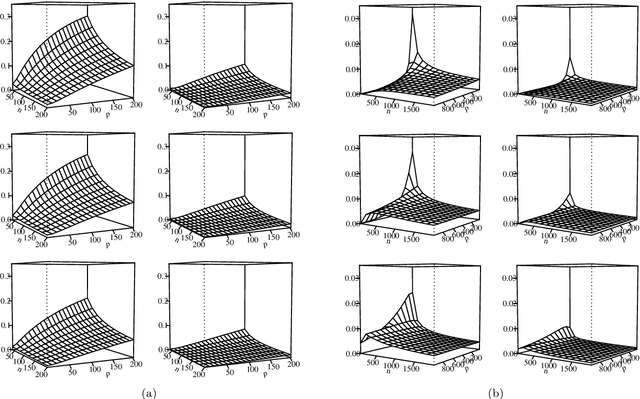
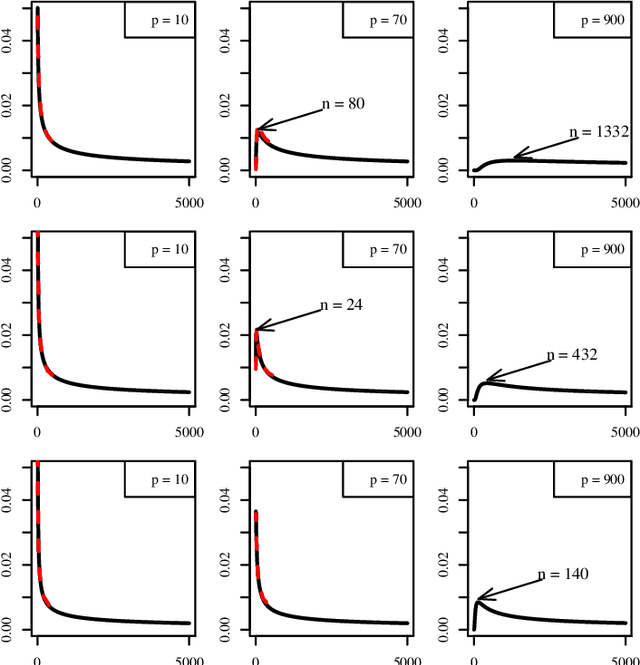
The most important aspect of any classifier is its error rate, because this quantifies its predictive capacity. Thus, the accuracy of error estimation is critical. Error estimation is problematic in small-sample classifier design because the error must be estimated using the same data from which the classifier has been designed. Use of prior knowledge, in the form of a prior distribution on an uncertainty class of feature-label distributions to which the true, but unknown, feature-distribution belongs, can facilitate accurate error estimation (in the mean-square sense) in circumstances where accurate completely model-free error estimation is impossible. This paper provides analytic asymptotically exact finite-sample approximations for various performance metrics of the resulting Bayesian Minimum Mean-Square-Error (MMSE) error estimator in the case of linear discriminant analysis (LDA) in the multivariate Gaussian model. These performance metrics include the first, second, and cross moments of the Bayesian MMSE error estimator with the true error of LDA, and therefore, the Root-Mean-Square (RMS) error of the estimator. We lay down the theoretical groundwork for Kolmogorov double-asymptotics in a Bayesian setting, which enables us to derive asymptotic expressions of the desired performance metrics. From these we produce analytic finite-sample approximations and demonstrate their accuracy via numerical examples. Various examples illustrate the behavior of these approximations and their use in determining the necessary sample size to achieve a desired RMS. The Supplementary Material contains derivations for some equations and added figures.