Optimal Bayesian Transfer Learning
Paper and Code
May 25, 2018
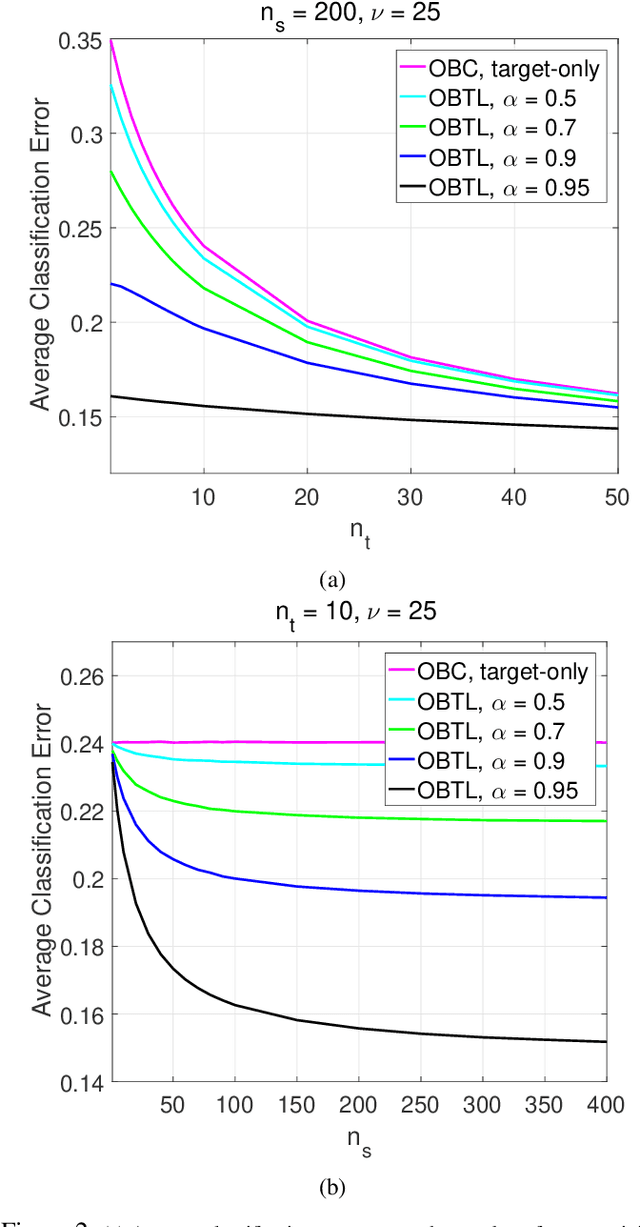
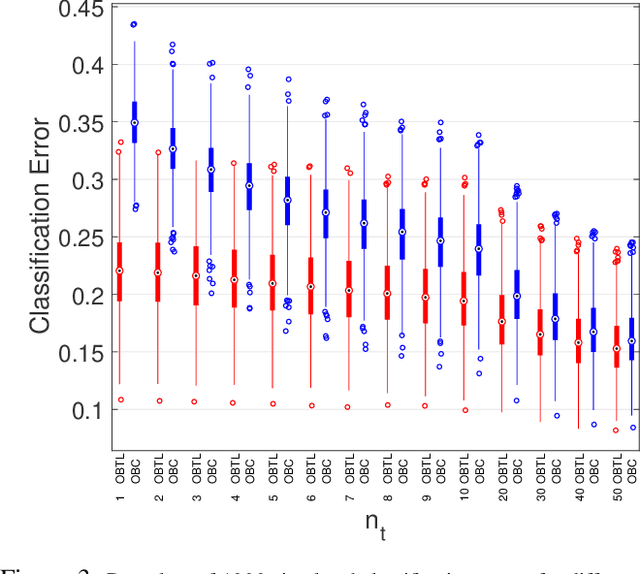
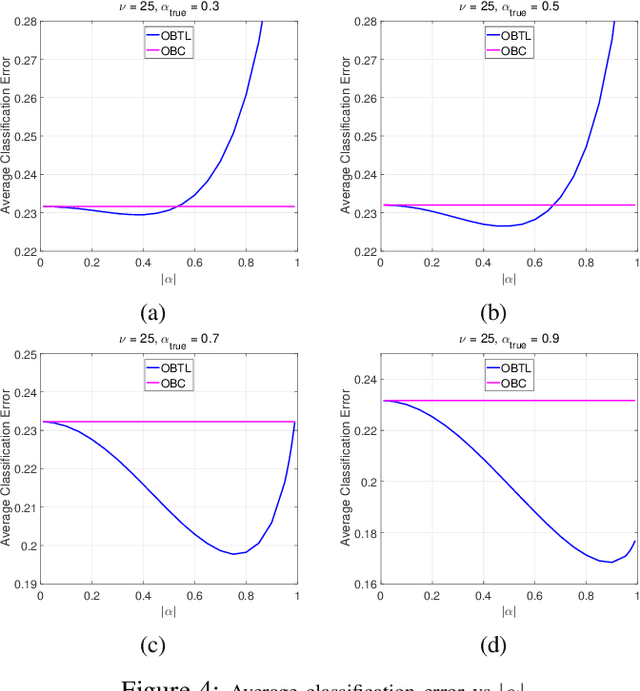
Transfer learning has recently attracted significant research attention, as it simultaneously learns from different source domains, which have plenty of labeled data, and transfers the relevant knowledge to the target domain with limited labeled data to improve the prediction performance. We propose a Bayesian transfer learning framework where the source and target domains are related through the joint prior density of the model parameters. The modeling of joint prior densities enables better understanding of the "transferability" between domains. We define a joint Wishart density for the precision matrices of the Gaussian feature-label distributions in the source and target domains to act like a bridge that transfers the useful information of the source domain to help classification in the target domain by improving the target posteriors. Using several theorems in multivariate statistics, the posteriors and posterior predictive densities are derived in closed forms with hypergeometric functions of matrix argument, leading to our novel closed-form and fast Optimal Bayesian Transfer Learning (OBTL) classifier. Experimental results on both synthetic and real-world benchmark data confirm the superb performance of the OBTL compared to the other state-of-the-art transfer learning and domain adaptation methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge