Bayesian multi-domain learning for cancer subtype discovery from next-generation sequencing count data

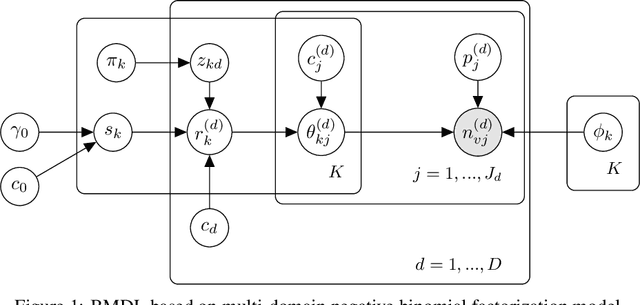
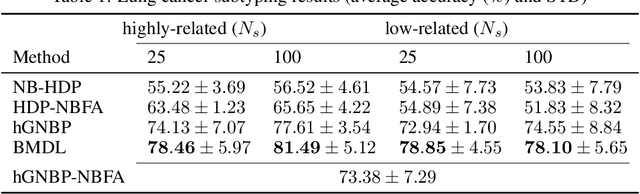
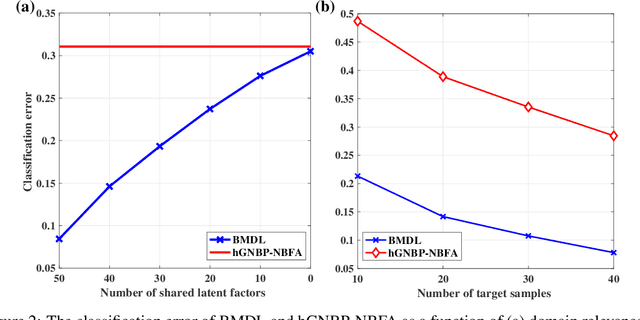
Precision medicine aims for personalized prognosis and therapeutics by utilizing recent genome-scale high-throughput profiling techniques, including next-generation sequencing (NGS). However, translating NGS data faces several challenges. First, NGS count data are often overdispersed, requiring appropriate modeling. Second, compared to the number of involved molecules and system complexity, the number of available samples for studying complex disease, such as cancer, is often limited, especially considering disease heterogeneity. The key question is whether we may integrate available data from all different sources or domains to achieve reproducible disease prognosis based on NGS count data. In this paper, we develop a Bayesian Multi-Domain Learning (BMDL) model that derives domain-dependent latent representations of overdispersed count data based on hierarchical negative binomial factorization for accurate cancer subtyping even if the number of samples for a specific cancer type is small. Experimental results from both our simulated and NGS datasets from The Cancer Genome Atlas (TCGA) demonstrate the promising potential of BMDL for effective multi-domain learning without "negative transfer" effects often seen in existing multi-task learning and transfer learning methods.

Optimal Bayesian Transfer Learning

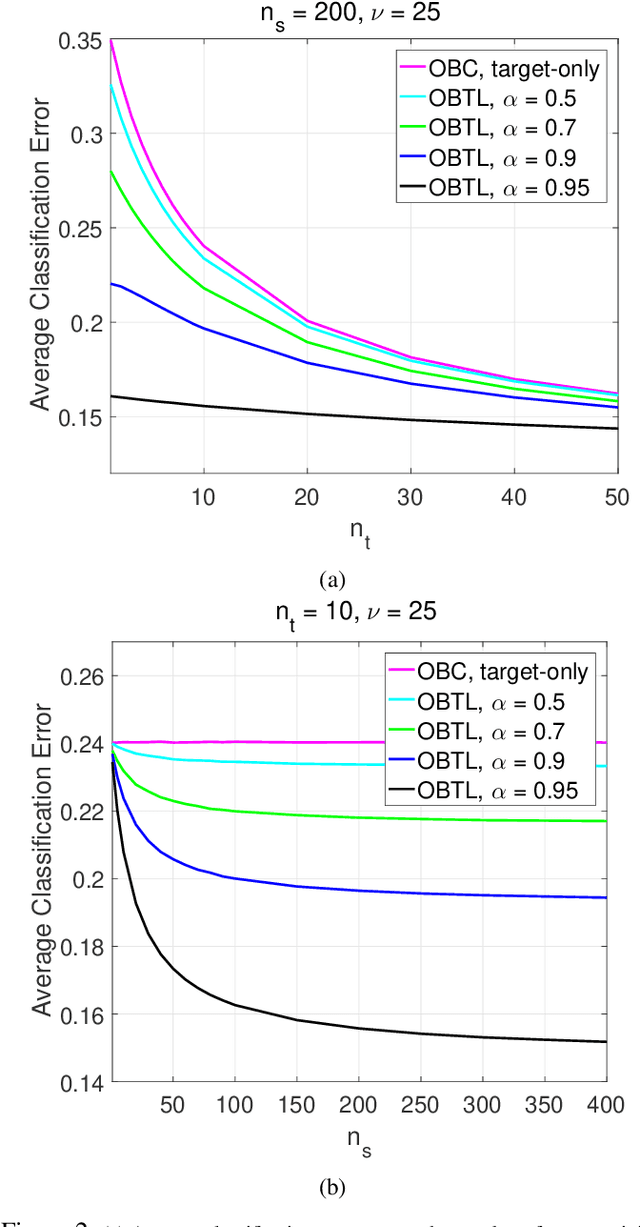
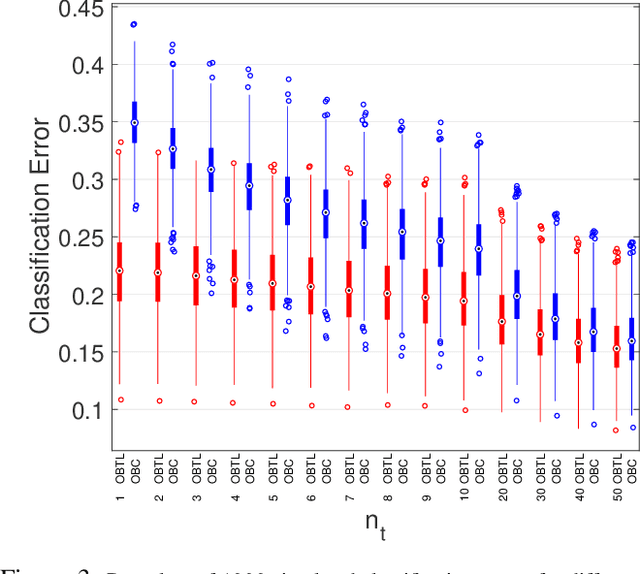
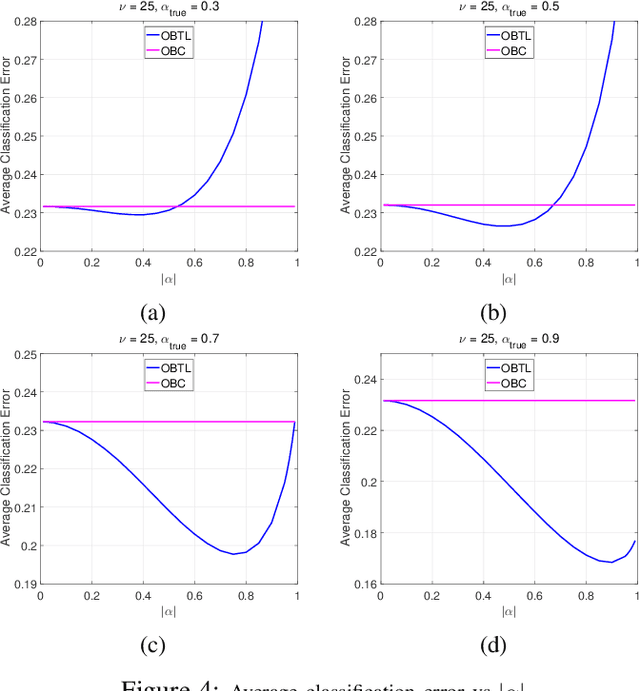
Transfer learning has recently attracted significant research attention, as it simultaneously learns from different source domains, which have plenty of labeled data, and transfers the relevant knowledge to the target domain with limited labeled data to improve the prediction performance. We propose a Bayesian transfer learning framework where the source and target domains are related through the joint prior density of the model parameters. The modeling of joint prior densities enables better understanding of the "transferability" between domains. We define a joint Wishart density for the precision matrices of the Gaussian feature-label distributions in the source and target domains to act like a bridge that transfers the useful information of the source domain to help classification in the target domain by improving the target posteriors. Using several theorems in multivariate statistics, the posteriors and posterior predictive densities are derived in closed forms with hypergeometric functions of matrix argument, leading to our novel closed-form and fast Optimal Bayesian Transfer Learning (OBTL) classifier. Experimental results on both synthetic and real-world benchmark data confirm the superb performance of the OBTL compared to the other state-of-the-art transfer learning and domain adaptation methods.