On the Consistency of Optimal Bayesian Feature Selection in the Presence of Correlations

Optimal Bayesian feature selection (OBFS) is a multivariate supervised screening method designed from the ground up for biomarker discovery. In this work, we prove that Gaussian OBFS is strongly consistent under mild conditions, and provide rates of convergence for key posteriors in the framework. These results are of enormous importance, since they identify precisely what features are selected by OBFS asymptotically, characterize the relative rates of convergence for posteriors on different types of features, provide conditions that guarantee convergence, justify the use of OBFS when its internal assumptions are invalid, and set the stage for understanding the asymptotic behavior of other algorithms based on the OBFS framework.

Theory of Optimal Bayesian Feature Filtering

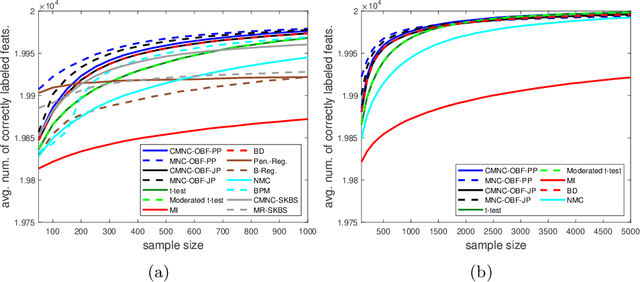
Optimal Bayesian feature filtering (OBF) is a supervised screening method designed for biomarker discovery. In this article, we prove two major theoretical properties of OBF. First, optimal Bayesian feature selection under a general family of Bayesian models reduces to filtering if and only if the underlying Bayesian model assumes all features are mutually independent. Therefore, OBF is optimal if and only if one assumes all features are mutually independent, and OBF is the only filter method that is optimal under at least one model in the general Bayesian framework. Second, OBF under independent Gaussian models is consistent under very mild conditions, including cases where the data is non-Gaussian with correlated features. This result provides conditions where OBF is guaranteed to identify the correct feature set given enough data, and it justifies the use of OBF in non-design settings where its assumptions are invalid.

Optimal Clustering under Uncertainty

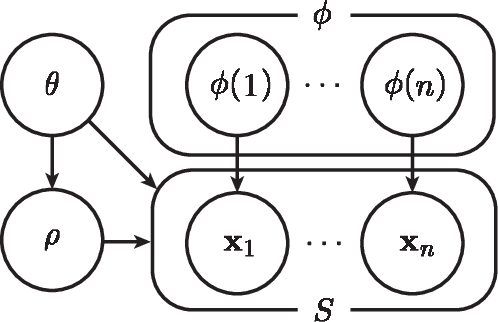
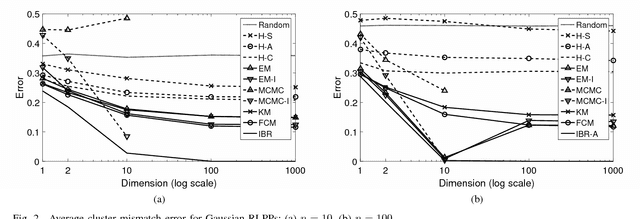
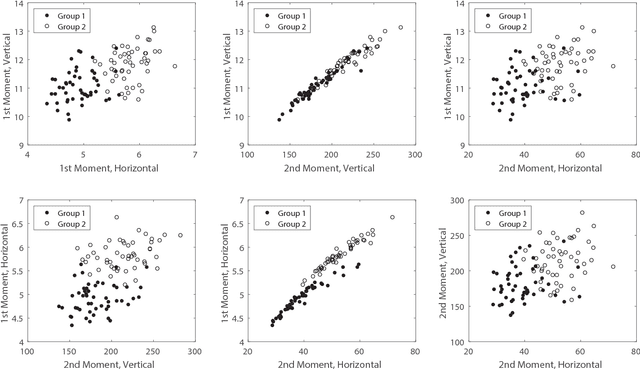
Classical clustering algorithms typically either lack an underlying probability framework to make them predictive or focus on parameter estimation rather than defining and minimizing a notion of error. Recent work addresses these issues by developing a probabilistic framework based on the theory of random labeled point processes and characterizing a Bayes clusterer that minimizes the number of misclustered points. The Bayes clusterer is analogous to the Bayes classifier. Whereas determining a Bayes classifier requires full knowledge of the feature-label distribution, deriving a Bayes clusterer requires full knowledge of the point process. When uncertain of the point process, one would like to find a robust clusterer that is optimal over the uncertainty, just as one may find optimal robust classifiers with uncertain feature-label distributions. Herein, we derive an optimal robust clusterer by first finding an effective random point process that incorporates all randomness within its own probabilistic structure and from which a Bayes clusterer can be derived that provides an optimal robust clusterer relative to the uncertainty. This is analogous to the use of effective class-conditional distributions in robust classification. After evaluating the performance of robust clusterers in synthetic mixtures of Gaussians models, we apply the framework to granular imaging, where we make use of the asymptotic granulometric moment theory for granular images to relate robust clustering theory to the application.