Adaptive Group Testing with Mismatched Models
Paper and Code
Oct 05, 2021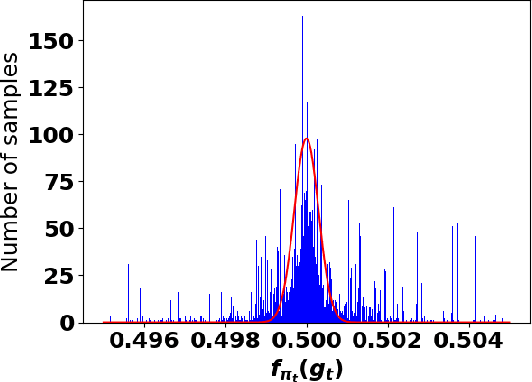
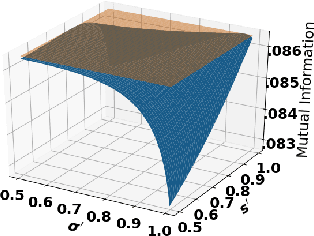
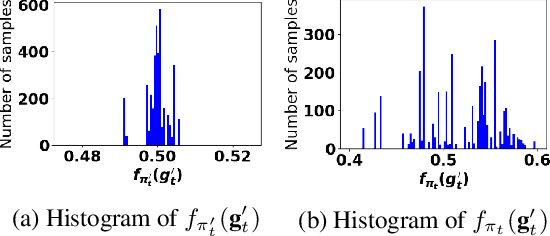
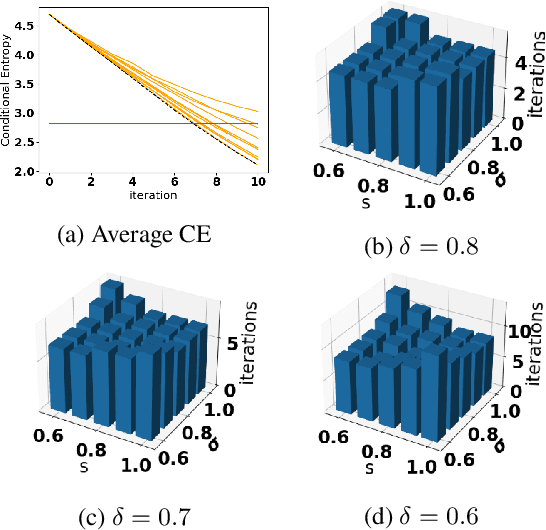
Accurate detection of infected individuals is one of the critical steps in stopping any pandemic. When the underlying infection rate of the disease is low, testing people in groups, instead of testing each individual in the population, can be more efficient. In this work, we consider noisy adaptive group testing design with specific test sensitivity and specificity that select the optimal group given previous test results based on pre-selected utility function. As in prior studies on group testing, we model this problem as a sequential Bayesian Optimal Experimental Design (BOED) to adaptively design the groups for each test. We analyze the required number of group tests when using the updated posterior on the infection status and the corresponding Mutual Information (MI) as our utility function for selecting new groups. More importantly, we study how the potential bias on the ground-truth noise of group tests may affect the group testing sample complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge