Path-Guided Particle-based Sampling

Particle-based Bayesian inference methods by sampling from a partition-free target (posterior) distribution, e.g., Stein variational gradient descent (SVGD), have attracted significant attention. We propose a path-guided particle-based sampling~(PGPS) method based on a novel Log-weighted Shrinkage (LwS) density path linking an initial distribution to the target distribution. We propose to utilize a Neural network to learn a vector field motivated by the Fokker-Planck equation of the designed density path. Particles, initiated from the initial distribution, evolve according to the ordinary differential equation defined by the vector field. The distribution of these particles is guided along a density path from the initial distribution to the target distribution. The proposed LwS density path allows for an efficient search of modes of the target distribution while canonical methods fail. We theoretically analyze the Wasserstein distance of the distribution of the PGPS-generated samples and the target distribution due to approximation and discretization errors. Practically, the proposed PGPS-LwS method demonstrates higher Bayesian inference accuracy and better calibration ability in experiments conducted on both synthetic and real-world Bayesian learning tasks, compared to baselines, such as SVGD and Langevin dynamics, etc.

Understanding Uncertainty-based Active Learning Under Model Mismatch

Instead of randomly acquiring training data points, Uncertainty-based Active Learning (UAL) operates by querying the label(s) of pivotal samples from an unlabeled pool selected based on the prediction uncertainty, thereby aiming at minimizing the labeling cost for model training. The efficacy of UAL critically depends on the model capacity as well as the adopted uncertainty-based acquisition function. Within the context of this study, our analytical focus is directed toward comprehending how the capacity of the machine learning model may affect UAL efficacy. Through theoretical analysis, comprehensive simulations, and empirical studies, we conclusively demonstrate that UAL can lead to worse performance in comparison with random sampling when the machine learning model class has low capacity and is unable to cover the underlying ground truth. In such situations, adopting acquisition functions that directly target estimating the prediction performance may be beneficial for improving the performance of UAL.

GFlowNet Training by Policy Gradients

Generative Flow Networks (GFlowNets) have been shown effective to generate combinatorial objects with desired properties. We here propose a new GFlowNet training framework, with policy-dependent rewards, that bridges keeping flow balance of GFlowNets to optimizing the expected accumulated reward in traditional Reinforcement-Learning (RL). This enables the derivation of new policy-based GFlowNet training methods, in contrast to existing ones resembling value-based RL. It is known that the design of backward policies in GFlowNet training affects efficiency. We further develop a coupled training strategy that jointly solves GFlowNet forward policy training and backward policy design. Performance analysis is provided with a theoretical guarantee of our policy-based GFlowNet training. Experiments on both simulated and real-world datasets verify that our policy-based strategies provide advanced RL perspectives for robust gradient estimation to improve GFlowNet performance.

Adaptive Group Testing with Mismatched Models

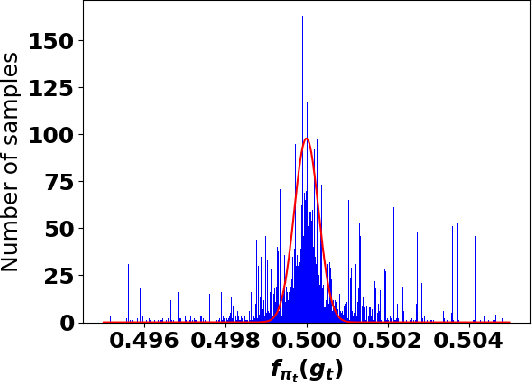
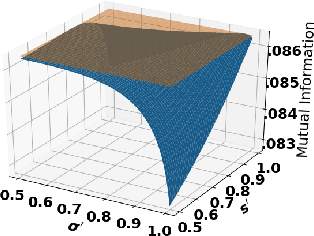
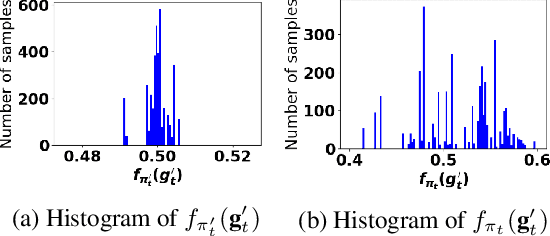
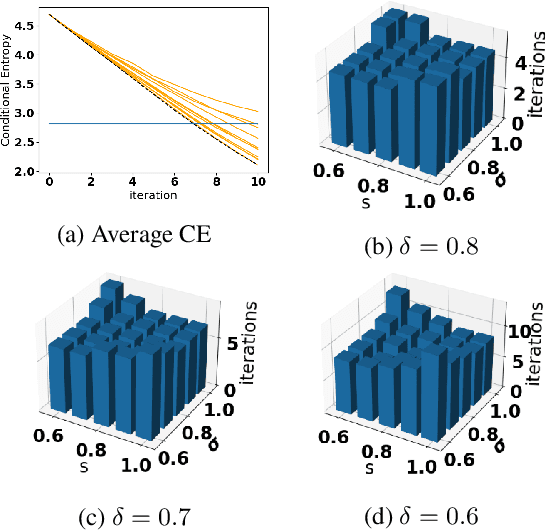
Accurate detection of infected individuals is one of the critical steps in stopping any pandemic. When the underlying infection rate of the disease is low, testing people in groups, instead of testing each individual in the population, can be more efficient. In this work, we consider noisy adaptive group testing design with specific test sensitivity and specificity that select the optimal group given previous test results based on pre-selected utility function. As in prior studies on group testing, we model this problem as a sequential Bayesian Optimal Experimental Design (BOED) to adaptively design the groups for each test. We analyze the required number of group tests when using the updated posterior on the infection status and the corresponding Mutual Information (MI) as our utility function for selecting new groups. More importantly, we study how the potential bias on the ground-truth noise of group tests may affect the group testing sample complexity.