Graph Positional Autoencoders as Self-supervised Learners

Graph self-supervised learning seeks to learn effective graph representations without relying on labeled data. Among various approaches, graph autoencoders (GAEs) have gained significant attention for their efficiency and scalability. Typically, GAEs take incomplete graphs as input and predict missing elements, such as masked nodes or edges. While effective, our experimental investigation reveals that traditional node or edge masking paradigms primarily capture low-frequency signals in the graph and fail to learn the expressive structural information. To address these issues, we propose Graph Positional Autoencoders (GraphPAE), which employs a dual-path architecture to reconstruct both node features and positions. Specifically, the feature path uses positional encoding to enhance the message-passing processing, improving GAE's ability to predict the corrupted information. The position path, on the other hand, leverages node representations to refine positions and approximate eigenvectors, thereby enabling the encoder to learn diverse frequency information. We conduct extensive experiments to verify the effectiveness of GraphPAE, including heterophilic node classification, graph property prediction, and transfer learning. The results demonstrate that GraphPAE achieves state-of-the-art performance and consistently outperforms baselines by a large margin.

Understanding Dataset Distillation via Spectral Filtering

Dataset distillation (DD) has emerged as a promising approach to compress datasets and speed up model training. However, the underlying connections among various DD methods remain largely unexplored. In this paper, we introduce UniDD, a spectral filtering framework that unifies diverse DD objectives. UniDD interprets each DD objective as a specific filter function that affects the eigenvalues of the feature-feature correlation (FFC) matrix and modulates the frequency components of the feature-label correlation (FLC) matrix. In this way, UniDD reveals that the essence of DD fundamentally lies in matching frequency-specific features. Moreover, according to the filter behaviors, we classify existing methods into low-frequency matching and high-frequency matching, encoding global texture and local details, respectively. However, existing methods rely on fixed filter functions throughout distillation, which cannot capture the low- and high-frequency information simultaneously. To address this limitation, we further propose Curriculum Frequency Matching (CFM), which gradually adjusts the filter parameter to cover both low- and high-frequency information of the FFC and FLC matrices. Extensive experiments on small-scale datasets, such as CIFAR-10/100, and large-scale datasets, including ImageNet-1K, demonstrate the superior performance of CFM over existing baselines and validate the practicality of UniDD.

Graph Condensation via Eigenbasis Matching

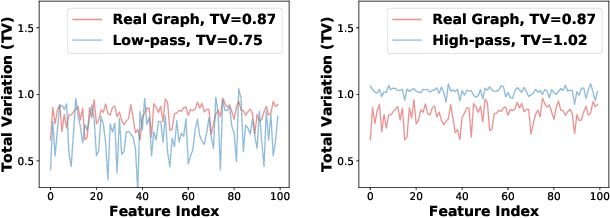
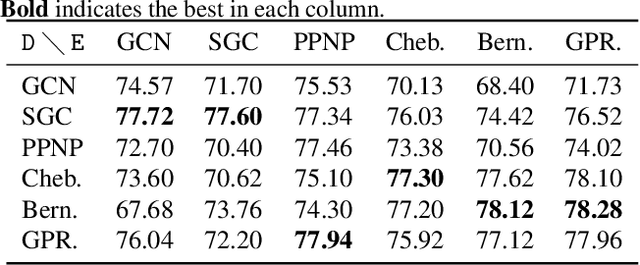
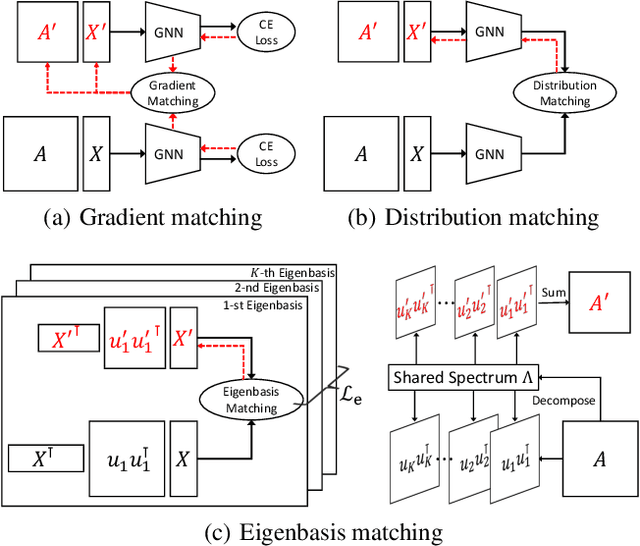
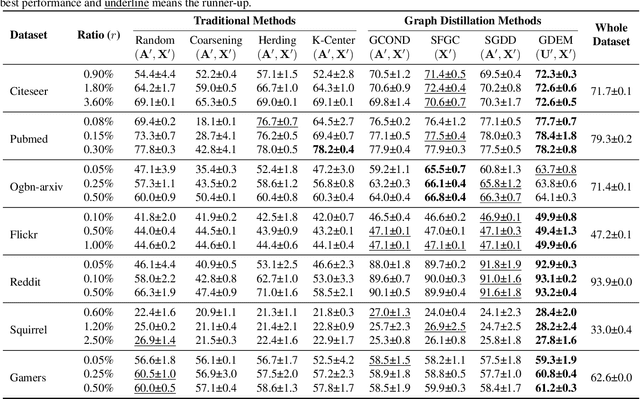
The increasing amount of graph data places requirements on the efficiency and scalability of graph neural networks (GNNs), despite their effectiveness in various graph-related applications. Recently, the emerging graph condensation (GC) sheds light on reducing the computational cost of GNNs from a data perspective. It aims to replace the real large graph with a significantly smaller synthetic graph so that GNNs trained on both graphs exhibit comparable performance. However, our empirical investigation reveals that existing GC methods suffer from poor generalization, i.e., different GNNs trained on the same synthetic graph have obvious performance gaps. What factors hinder the generalization of GC and how can we mitigate it? To answer this question, we commence with a detailed analysis and observe that GNNs will inject spectrum bias into the synthetic graph, resulting in a distribution shift. To tackle this issue, we propose eigenbasis matching for spectrum-free graph condensation, named GCEM, which has two key steps: First, GCEM matches the eigenbasis of the real and synthetic graphs, rather than the graph structure, which eliminates the spectrum bias of GNNs. Subsequently, GCEM leverages the spectrum of the real graph and the synthetic eigenbasis to construct the synthetic graph, thereby preserving the essential structural information. We theoretically demonstrate that the synthetic graph generated by GCEM maintains the spectral similarity, i.e., total variation, of the real graph. Extensive experiments conducted on five graph datasets verify that GCEM not only achieves state-of-the-art performance over baselines but also significantly narrows the performance gaps between different GNNs.

Data-centric Graph Learning: A Survey

The history of artificial intelligence (AI) has witnessed the significant impact of high-quality data on various deep learning models, such as ImageNet for AlexNet and ResNet. Recently, instead of designing more complex neural architectures as model-centric approaches, the attention of AI community has shifted to data-centric ones, which focuses on better processing data to strengthen the ability of neural models. Graph learning, which operates on ubiquitous topological data, also plays an important role in the era of deep learning. In this survey, we comprehensively review graph learning approaches from the data-centric perspective, and aim to answer two crucial questions: (1) when to modify graph data and (2) how to modify graph data to unlock the potential of various graph models. Accordingly, we propose a novel taxonomy based on the stages in the graph learning pipeline, and highlight the processing methods for different data structures in the graph data, i.e., topology, feature and label. Furthermore, we analyze some potential problems embedded in graph data and discuss how to solve them in a data-centric manner. Finally, we provide some promising future directions for data-centric graph learning.

Specformer: Spectral Graph Neural Networks Meet Transformers

Spectral graph neural networks (GNNs) learn graph representations via spectral-domain graph convolutions. However, most existing spectral graph filters are scalar-to-scalar functions, i.e., mapping a single eigenvalue to a single filtered value, thus ignoring the global pattern of the spectrum. Furthermore, these filters are often constructed based on some fixed-order polynomials, which have limited expressiveness and flexibility. To tackle these issues, we introduce Specformer, which effectively encodes the set of all eigenvalues and performs self-attention in the spectral domain, leading to a learnable set-to-set spectral filter. We also design a decoder with learnable bases to enable non-local graph convolution. Importantly, Specformer is equivariant to permutation. By stacking multiple Specformer layers, one can build a powerful spectral GNN. On synthetic datasets, we show that our Specformer can better recover ground-truth spectral filters than other spectral GNNs. Extensive experiments of both node-level and graph-level tasks on real-world graph datasets show that our Specformer outperforms state-of-the-art GNNs and learns meaningful spectrum patterns. Code and data are available at https://github.com/bdy9527/Specformer.

A Survey on Spectral Graph Neural Networks

Graph neural networks (GNNs) have attracted considerable attention from the research community. It is well established that GNNs are usually roughly divided into spatial and spectral methods. Despite that spectral GNNs play an important role in both graph signal processing and graph representation learning, existing studies are biased toward spatial approaches, and there is no comprehensive review on spectral GNNs so far. In this paper, we summarize the recent development of spectral GNNs, including model, theory, and application. Specifically, we first discuss the connection between spatial GNNs and spectral GNNs, which shows that spectral GNNs can capture global information and have better expressiveness and interpretability. Next, we categorize existing spectral GNNs according to the spectrum information they use, \ie, eigenvalues or eigenvectors. In addition, we review major theoretical results and applications of spectral GNNs, followed by a quantitative experiment to benchmark some popular spectral GNNs. Finally, we conclude the paper with some future directions.

Revisiting Graph Contrastive Learning from the Perspective of Graph Spectrum

Graph Contrastive Learning (GCL), learning the node representations by augmenting graphs, has attracted considerable attentions. Despite the proliferation of various graph augmentation strategies, some fundamental questions still remain unclear: what information is essentially encoded into the learned representations by GCL? Are there some general graph augmentation rules behind different augmentations? If so, what are they and what insights can they bring? In this paper, we answer these questions by establishing the connection between GCL and graph spectrum. By an experimental investigation in spectral domain, we firstly find the General grAph augMEntation (GAME) rule for GCL, i.e., the difference of the high-frequency parts between two augmented graphs should be larger than that of low-frequency parts. This rule reveals the fundamental principle to revisit the current graph augmentations and design new effective graph augmentations. Then we theoretically prove that GCL is able to learn the invariance information by contrastive invariance theorem, together with our GAME rule, for the first time, we uncover that the learned representations by GCL essentially encode the low-frequency information, which explains why GCL works. Guided by this rule, we propose a spectral graph contrastive learning module (SpCo), which is a general and GCL-friendly plug-in. We combine it with different existing GCL models, and extensive experiments well demonstrate that it can further improve the performances of a wide variety of different GCL methods.

Beyond Low-frequency Information in Graph Convolutional Networks

Graph neural networks (GNNs) have been proven to be effective in various network-related tasks. Most existing GNNs usually exploit the low-frequency signals of node features, which gives rise to one fundamental question: is the low-frequency information all we need in the real world applications? In this paper, we first present an experimental investigation assessing the roles of low-frequency and high-frequency signals, where the results clearly show that exploring low-frequency signal only is distant from learning an effective node representation in different scenarios. How can we adaptively learn more information beyond low-frequency information in GNNs? A well-informed answer can help GNNs enhance the adaptability. We tackle this challenge and propose a novel Frequency Adaptation Graph Convolutional Networks (FAGCN) with a self-gating mechanism, which can adaptively integrate different signals in the process of message passing. For a deeper understanding, we theoretically analyze the roles of low-frequency signals and high-frequency signals on learning node representations, which further explains why FAGCN can perform well on different types of networks. Extensive experiments on six real-world networks validate that FAGCN not only alleviates the over-smoothing problem, but also has advantages over the state-of-the-arts.

A Survey on Heterogeneous Graph Embedding: Methods, Techniques, Applications and Sources

Heterogeneous graphs (HGs) also known as heterogeneous information networks have become ubiquitous in real-world scenarios; therefore, HG embedding, which aims to learn representations in a lower-dimension space while preserving the heterogeneous structures and semantics for downstream tasks (e.g., node/graph classification, node clustering, link prediction), has drawn considerable attentions in recent years. In this survey, we perform a comprehensive review of the recent development on HG embedding methods and techniques. We first introduce the basic concepts of HG and discuss the unique challenges brought by the heterogeneity for HG embedding in comparison with homogeneous graph representation learning; and then we systemically survey and categorize the state-of-the-art HG embedding methods based on the information they used in the learning process to address the challenges posed by the HG heterogeneity. In particular, for each representative HG embedding method, we provide detailed introduction and further analyze its pros and cons; meanwhile, we also explore the transformativeness and applicability of different types of HG embedding methods in the real-world industrial environments for the first time. In addition, we further present several widely deployed systems that have demonstrated the success of HG embedding techniques in resolving real-world application problems with broader impacts. To facilitate future research and applications in this area, we also summarize the open-source code, existing graph learning platforms and benchmark datasets. Finally, we explore the additional issues and challenges of HG embedding and forecast the future research directions in this field.

AM-GCN: Adaptive Multi-channel Graph Convolutional Networks

Graph Convolutional Networks (GCNs) have gained great popularity in tackling various analytics tasks on graph and network data. However, some recent studies raise concerns about whether GCNs can optimally integrate node features and topological structures in a complex graph with rich information. In this paper, we first present an experimental investigation. Surprisingly, our experimental results clearly show that the capability of the state-of-the-art GCNs in fusing node features and topological structures is distant from optimal or even satisfactory. The weakness may severely hinder the capability of GCNs in some classification tasks, since GCNs may not be able to adaptively learn some deep correlation information between topological structures and node features. Can we remedy the weakness and design a new type of GCNs that can retain the advantages of the state-of-the-art GCNs and, at the same time, enhance the capability of fusing topological structures and node features substantially? We tackle the challenge and propose an adaptive multi-channel graph convolutional networks for semi-supervised classification (AM-GCN). The central idea is that we extract the specific and common embeddings from node features, topological structures, and their combinations simultaneously, and use the attention mechanism to learn adaptive importance weights of the embeddings. Our extensive experiments on benchmark data sets clearly show that AM-GCN extracts the most correlated information from both node features and topological structures substantially, and improves the classification accuracy with a clear margin.