Graph Condensation via Eigenbasis Matching

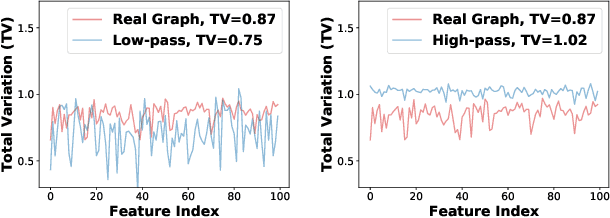
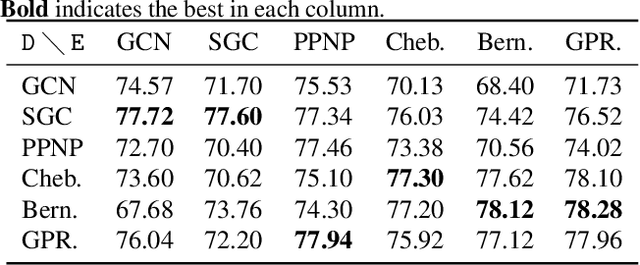
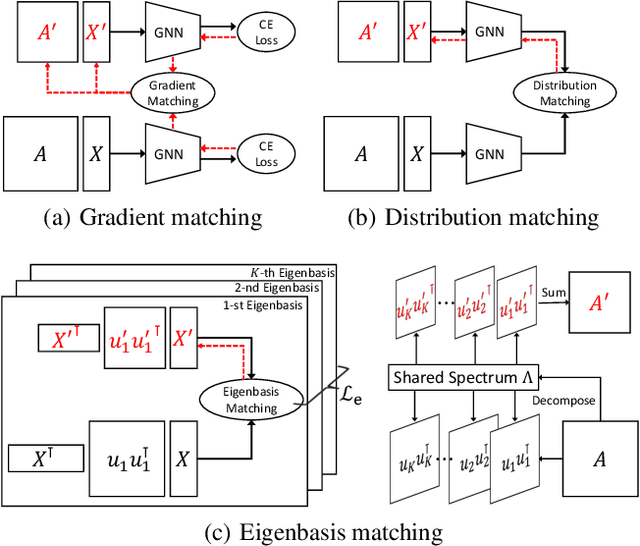
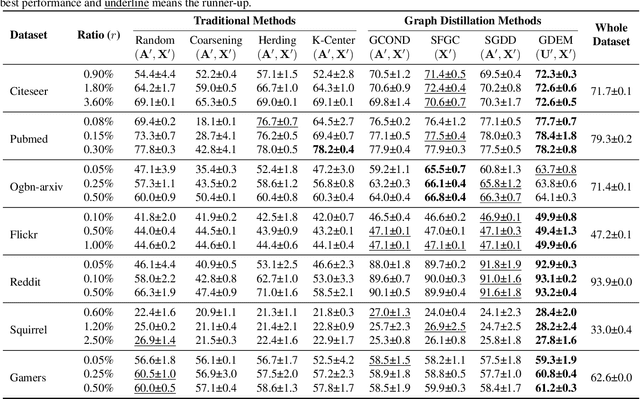
The increasing amount of graph data places requirements on the efficiency and scalability of graph neural networks (GNNs), despite their effectiveness in various graph-related applications. Recently, the emerging graph condensation (GC) sheds light on reducing the computational cost of GNNs from a data perspective. It aims to replace the real large graph with a significantly smaller synthetic graph so that GNNs trained on both graphs exhibit comparable performance. However, our empirical investigation reveals that existing GC methods suffer from poor generalization, i.e., different GNNs trained on the same synthetic graph have obvious performance gaps. What factors hinder the generalization of GC and how can we mitigate it? To answer this question, we commence with a detailed analysis and observe that GNNs will inject spectrum bias into the synthetic graph, resulting in a distribution shift. To tackle this issue, we propose eigenbasis matching for spectrum-free graph condensation, named GCEM, which has two key steps: First, GCEM matches the eigenbasis of the real and synthetic graphs, rather than the graph structure, which eliminates the spectrum bias of GNNs. Subsequently, GCEM leverages the spectrum of the real graph and the synthetic eigenbasis to construct the synthetic graph, thereby preserving the essential structural information. We theoretically demonstrate that the synthetic graph generated by GCEM maintains the spectral similarity, i.e., total variation, of the real graph. Extensive experiments conducted on five graph datasets verify that GCEM not only achieves state-of-the-art performance over baselines but also significantly narrows the performance gaps between different GNNs.