Kan Extensions in Data Science and Machine Learning

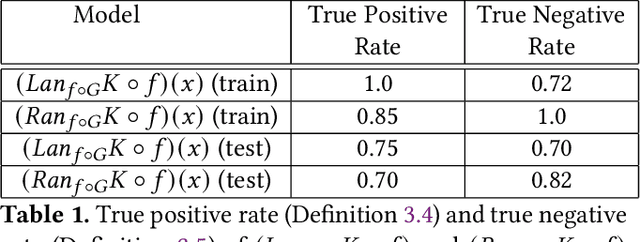
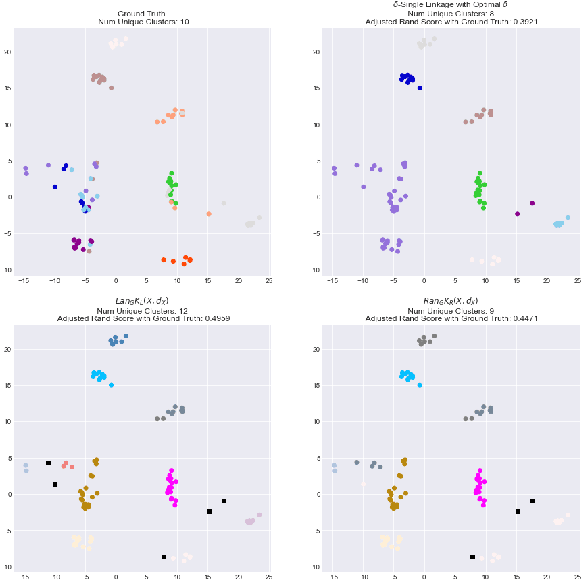
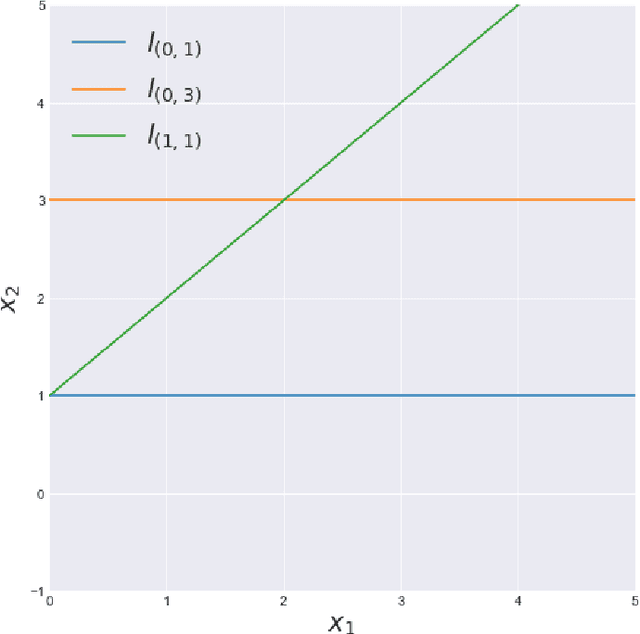
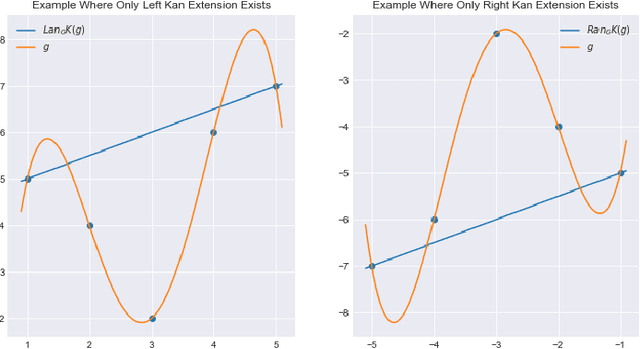
A common problem in data science is "use this function defined over this small set to generate predictions over that larger set." Extrapolation, interpolation, statistical inference and forecasting all reduce to this problem. The Kan extension is a powerful tool in category theory that generalizes this notion. In this work we explore several applications of Kan extensions to data science. We begin by deriving a simple classification algorithm as a Kan extension and experimenting with this algorithm on real data. Next, we use the Kan extension to derive a procedure for learning clustering algorithms from labels and explore the performance of this procedure on real data. We then investigate how Kan extensions can be used to learn a general mapping from datasets of labeled examples to functions and to approximate a complex function with a simpler one.

Generalized Optimization: A First Step Towards Category Theoretic Learning Theory

The Cartesian reverse derivative is a categorical generalization of reverse-mode automatic differentiation. We use this operator to generalize several optimization algorithms, including a straightforward generalization of gradient descent and a novel generalization of Newton's method. We then explore which properties of these algorithms are preserved in this generalized setting. First, we show that the transformation invariances of these algorithms are preserved: while generalized Newton's method is invariant to all invertible linear transformations, generalized gradient descent is invariant only to orthogonal linear transformations. Next, we show that we can express the change in loss of generalized gradient descent with an inner product-like expression, thereby generalizing the non-increasing and convergence properties of the gradient descent optimization flow. Finally, we include several numerical experiments to illustrate the ideas in the paper and demonstrate how we can use them to optimize polynomial functions over an ordered ring.

Category Theory in Machine Learning

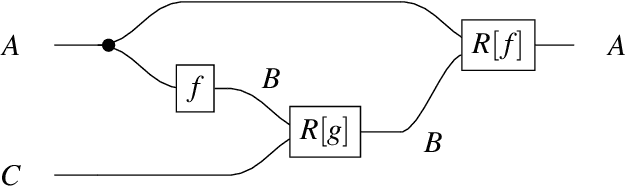
Over the past two decades machine learning has permeated almost every realm of technology. At the same time, many researchers have begun using category theory as a unifying language, facilitating communication between different scientific disciplines. It is therefore unsurprising that there is a burgeoning interest in applying category theory to machine learning. We aim to document the motivations, goals and common themes across these applications. We touch on gradient-based learning, probability, and equivariant learning.

Lessons Learned Addressing Dataset Bias in Model-Based Candidate Generation at Twitter

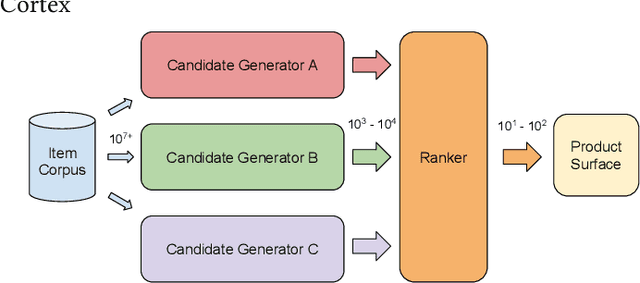
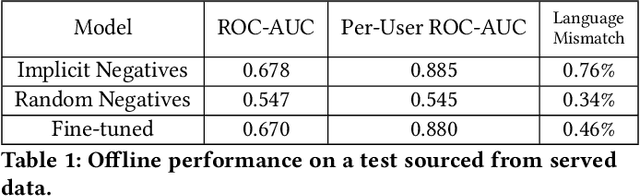
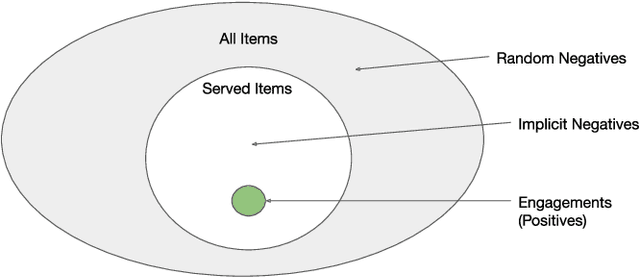
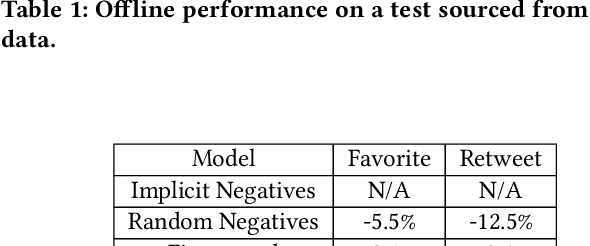
Traditionally, heuristic methods are used to generate candidates for large scale recommender systems. Model-based candidate generation promises multiple potential advantages, primarily that we can explicitly optimize the same objective as the downstream ranking model. However, large scale model-based candidate generation approaches suffer from dataset bias problems caused by the infeasibility of obtaining representative data on very irrelevant candidates. Popular techniques to correct dataset bias, such as inverse propensity scoring, do not work well in the context of candidate generation. We first explore the dynamics of the dataset bias problem and then demonstrate how to use random sampling techniques to mitigate it. Finally, in a novel application of fine-tuning, we show performance gains when applying our candidate generation system to Twitter's home timeline.

Flattening Multiparameter Hierarchical Clustering Functors

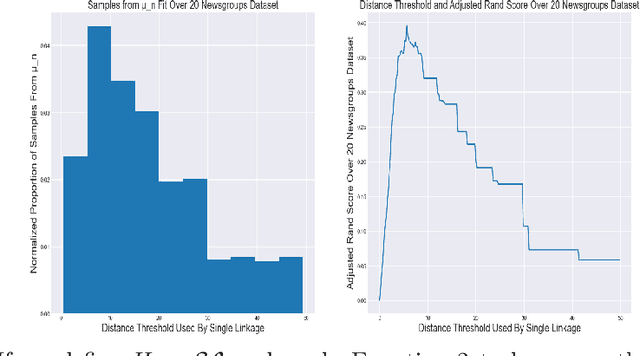
We bring together topological data analysis, applied category theory, and machine learning to study multiparameter hierarchical clustering. We begin by introducing a procedure for flattening multiparameter hierarchical clusterings. We demonstrate that this procedure is a functor from a category of multiparameter hierarchical partitions to a category of binary integer programs. We also include empirical results demonstrating its effectiveness. Next, we introduce a Bayesian update algorithm for learning clustering parameters from data. We demonstrate that the composition of this algorithm with our flattening procedure satisfies a consistency property.

Functorial Manifold Learning and Overlapping Clustering

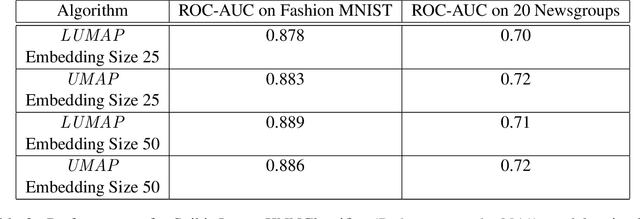
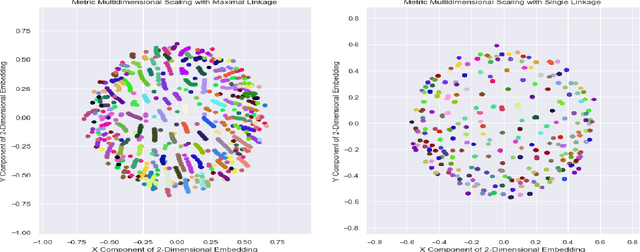
We adapt previous research on topological unsupervised learning to develop a unified functorial perspective on manifold learning and clustering. We first introduce overlapping hierachical clustering algorithms as functors and demonstrate that the maximal and single linkage clustering algorithms factor through an adaptation of the singular set functor. Next, we characterize manifold learning algorithms as functors that map uber-metric spaces to optimization objectives and factor through hierachical clustering functors. We use this characterization to prove refinement bounds on manifold learning loss functions and construct a hierarchy of manifold learning algorithms based on their invariants. We express several state of the art manifold learning algorithms as functors at different levels of this hierarchy, including Laplacian Eigenmaps, Metric Multidimensional Scaling, and UMAP. Finally, we experimentally demonstrate that this perspective enables us to derive and analyze novel manifold learning algorithms.

Tuning Word2vec for Large Scale Recommendation Systems

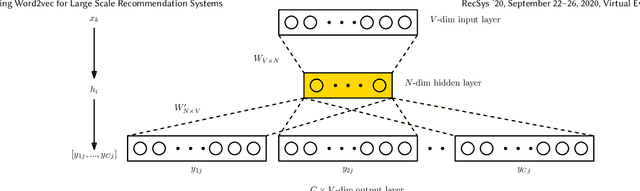
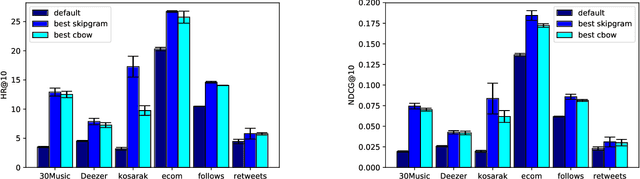
Word2vec is a powerful machine learning tool that emerged from Natural Lan-guage Processing (NLP) and is now applied in multiple domains, including recom-mender systems, forecasting, and network analysis. As Word2vec is often used offthe shelf, we address the question of whether the default hyperparameters are suit-able for recommender systems. The answer is emphatically no. In this paper, wefirst elucidate the importance of hyperparameter optimization and show that un-constrained optimization yields an average 221% improvement in hit rate over thedefault parameters. However, unconstrained optimization leads to hyperparametersettings that are very expensive and not feasible for large scale recommendationtasks. To this end, we demonstrate 138% average improvement in hit rate with aruntime budget-constrained hyperparameter optimization. Furthermore, to makehyperparameter optimization applicable for large scale recommendation problemswhere the target dataset is too large to search over, we investigate generalizinghyperparameters settings from samples. We show that applying constrained hy-perparameter optimization using only a 10% sample of the data still yields a 91%average improvement in hit rate over the default parameters when applied to thefull datasets. Finally, we apply hyperparameters learned using our method of con-strained optimization on a sample to the Who To Follow recommendation serviceat Twitter and are able to increase follow rates by 15%.

Categorical Stochastic Processes and Likelihood

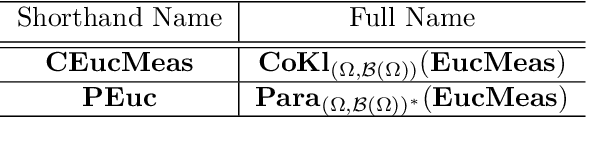
In this work we take a Category Theoretic perspective on the relationship between probabilistic modeling and function approximation. We begin by defining two extensions of function composition to stochastic process subordination: one based on the co-Kleisli category under the comonad (Omega x -) and one based on the parameterization of a category with a Lawvere theory. We show how these extensions relate to the category Stoch and other Markov Categories. Next, we apply the Para construction to extend stochastic processes to parameterized statistical models and we define a way to compose the likelihood functions of these models. We conclude with a demonstration of how the Maximum Likelihood Estimation procedure defines an identity-on-objects functor from the category of statistical models to the category of Learners. Code to accompany this paper can be found at https://github.com/dshieble/Categorical_Stochastic_Processes_and_Likelihood

Incremental Monoidal Grammars

In this work we define formal grammars in terms of free monoidal categories, along with a functor from the category of formal grammars to the category of automata. Generalising from the Booleans to arbitrary semirings, we extend our construction to weighted formal grammars and weighted automata. This allows us to link the categorical viewpoint on natural language to the standard machine learning notion of probabilistic language model.

Fighting Redundancy and Model Decay with Embeddings

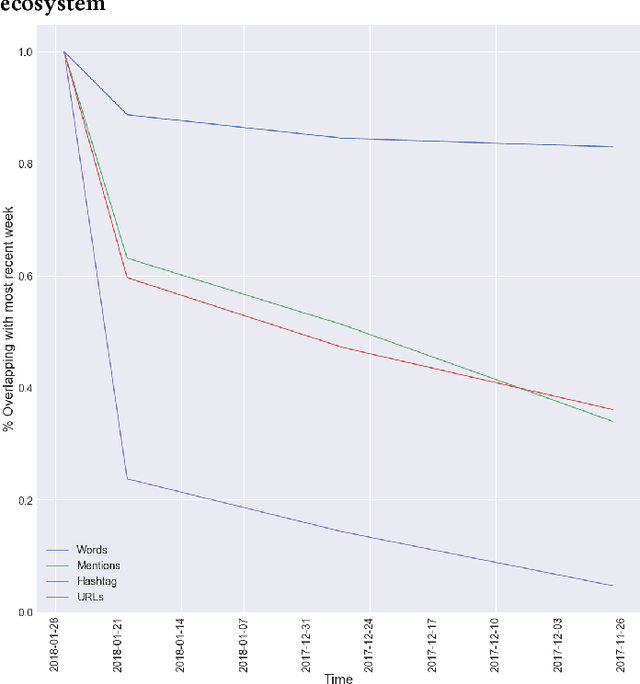
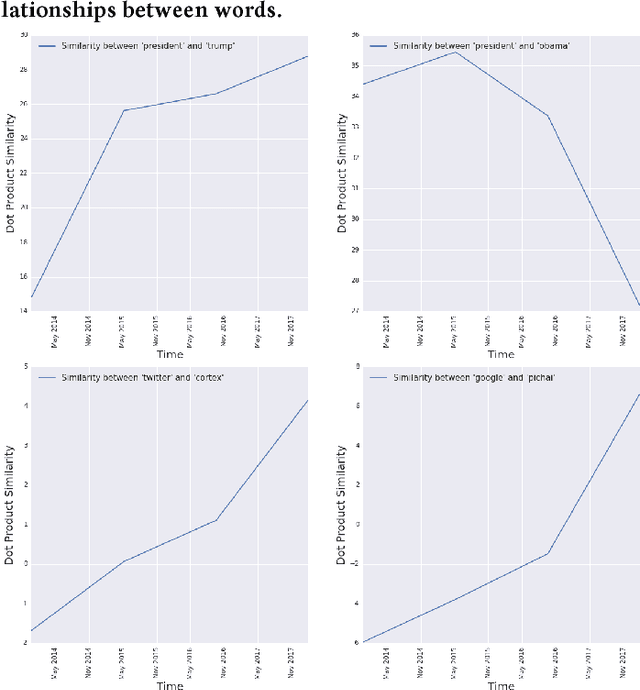
Every day, hundreds of millions of new Tweets containing over 40 languages of ever-shifting vernacular flow through Twitter. Models that attempt to extract insight from this firehose of information must face the torrential covariate shift that is endemic to the Twitter platform. While regularly-retrained algorithms can maintain performance in the face of this shift, fixed model features that fail to represent new trends and tokens can quickly become stale, resulting in performance degradation. To mitigate this problem we employ learned features, or embedding models, that can efficiently represent the most relevant aspects of a data distribution. Sharing these embedding models across teams can also reduce redundancy and multiplicatively increase cross-team modeling productivity. In this paper, we detail the commoditized tools, algorithms and pipelines that we have developed and are developing at Twitter to regularly generate high quality, up-to-date embeddings and share them broadly across the company.