Multimodal Structure-Aware Quantum Data Processing

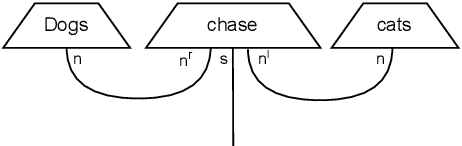
While large language models (LLMs) have advanced the field of natural language processing (NLP), their ``black box'' nature obscures their decision-making processes. To address this, researchers developed structured approaches using higher order tensors. These are able to model linguistic relations, but stall when training on classical computers due to their excessive size. Tensors are natural inhabitants of quantum systems and training on quantum computers provides a solution by translating text to variational quantum circuits. In this paper, we develop MultiQ-NLP: a framework for structure-aware data processing with multimodal text+image data. Here, ``structure'' refers to syntactic and grammatical relationships in language, as well as the hierarchical organization of visual elements in images. We enrich the translation with new types and type homomorphisms and develop novel architectures to represent structure. When tested on a main stream image classification task (SVO Probes), our best model showed a par performance with the state of the art classical models; moreover the best model was fully structured.

Developments in Sheaf-Theoretic Models of Natural Language Ambiguities

Sheaves are mathematical objects consisting of a base which constitutes a topological space and the data associated with each open set thereof, e.g. continuous functions defined on the open sets. Sheaves have originally been used in algebraic topology and logic. Recently, they have also modelled events such as physical experiments and natural language disambiguation processes. We extend the latter models from lexical ambiguities to discourse ambiguities arising from anaphora. To begin, we calculated a new measure of contextuality for a dataset of basic anaphoric discourses, resulting in a higher proportion of contextual models--82.9%--compared to previous work which only yielded 3.17% contextual models. Then, we show how an extension of the natural language processing challenge, known as the Winograd Schema, which involves anaphoric ambiguities can be modelled on the Bell-CHSH scenario with a contextual fraction of 0.096.

Towards Transparency in Coreference Resolution: A Quantum-Inspired Approach

Guided by grammatical structure, words compose to form sentences, and guided by discourse structure, sentences compose to form dialogues and documents. The compositional aspect of sentence and discourse units is often overlooked by machine learning algorithms. A recent initiative called Quantum Natural Language Processing (QNLP) learns word meanings as points in a Hilbert space and acts on them via a translation of grammatical structure into Parametrised Quantum Circuits (PQCs). Previous work extended the QNLP translation to discourse structure using points in a closure of Hilbert spaces. In this paper, we evaluate this translation on a Winograd-style pronoun resolution task. We train a Variational Quantum Classifier (VQC) for binary classification and implement an end-to-end pronoun resolution system. The simulations executed on IBMQ software converged with an F1 score of 87.20%. The model outperformed two out of three classical coreference resolution systems and neared state-of-the-art SpanBERT. A mixed quantum-classical model yet improved these results with an F1 score increase of around 6%.

Generalised Winograd Schema and its Contextuality

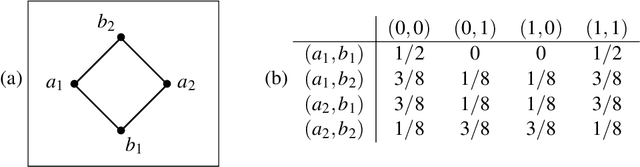
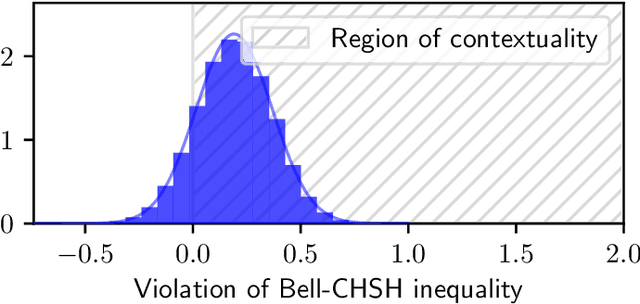
Ambiguities in natural language give rise to probability distributions over interpretations. The distributions are often over multiple ambiguous words at a time; a multiplicity which makes them a suitable topic for sheaf-theoretic models of quantum contextuality. Previous research showed that different quantitative measures of contextuality correlate well with Psycholinguistic research on lexical ambiguities. In this work, we focus on coreference ambiguities and investigate the Winograd Schema Challenge (WSC), a test proposed by Levesque in 2011 to evaluate the intelligence of machines. The WSC consists of a collection of multiple-choice questions that require disambiguating pronouns in sentences structured according to the Winograd schema, in a way that makes it difficult for machines to determine the correct referents but remains intuitive for human comprehension. In this study, we propose an approach that analogously models the Winograd schema as an experiment in quantum physics. However, we argue that the original Winograd Schema is inherently too simplistic to facilitate contextuality. We introduce a novel mechanism for generalising the schema, rendering it analogous to a Bell-CHSH measurement scenario. We report an instance of this generalised schema, complemented by the human judgements we gathered via a crowdsourcing platform. The resulting model violates the Bell-CHSH inequality by 0.192, thus exhibiting contextuality in a coreference resolution setting.

Proceedings Modalities in substructural logics: Applications at the interfaces of logic, language and computation

By calling into question the implicit structural rules that are taken for granted in classical logic, substructural logics have brought to the fore new forms of reasoning with applications in many interdisciplinary areas of interest. Modalities, in the substructural setting, provide the tools to control and finetune the logical resource management. The focus of the workshop is on applications in the areas of interest to the ESSLLI community, in particular logical approaches to natural language syntax and semantics and the dynamics of reasoning. The workshop is held with the support of the Horizon 2020 MSCA-Rise project MOSAIC .

A Model of Anaphoric Ambiguities using Sheaf Theoretic Quantum-like Contextuality and BERT

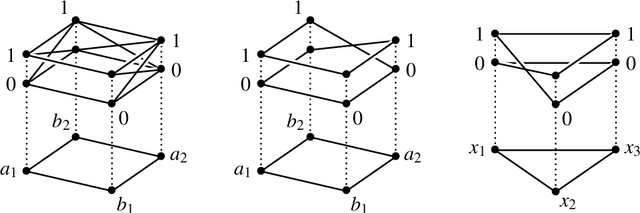
Ambiguities of natural language do not preclude us from using it and context helps in getting ideas across. They, nonetheless, pose a key challenge to the development of competent machines to understand natural language and use it as humans do. Contextuality is an unparalleled phenomenon in quantum mechanics, where different mathematical formalisms have been put forwards to understand and reason about it. In this paper, we construct a schema for anaphoric ambiguities that exhibits quantum-like contextuality. We use a recently developed criterion of sheaf-theoretic contextuality that is applicable to signalling models. We then take advantage of the neural word embedding engine BERT to instantiate the schema to natural language examples and extract probability distributions for the instances. As a result, plenty of sheaf-contextual examples were discovered in the natural language corpora BERT utilises. Our hope is that these examples will pave the way for future research and for finding ways to extend applications of quantum computing to natural language processing.

A Quantum Natural Language Processing Approach to Pronoun Resolution

We use the Lambek Calculus with soft sub-exponential modalities to model and reason about discourse relations such as anaphora and ellipsis. A semantics for this logic is obtained by using truncated Fock spaces, developed in our previous work. We depict these semantic computations via a new string diagram. The Fock Space semantics has the advantage that its terms are learnable from large corpora of data using machine learning and they can be experimented with on mainstream natural language tasks. Further, and thanks to an existing translation from vector spaces to quantum circuits, we can also learn these terms on quantum computers and their simulators, such as the IBMQ range. We extend the existing translation to Fock spaces and develop quantum circuit semantics for discourse relations. We then experiment with the IBMQ AerSimulations of these circuits in a definite pronoun resolution task, where the highest accuracies were recorded for models when the anaphora was resolved.

The Causal Structure of Semantic Ambiguities

Ambiguity is a natural language phenomenon occurring at different levels of syntax, semantics, and pragmatics. It is widely studied; in Psycholinguistics, for instance, we have a variety of competing studies for the human disambiguation processes. These studies are empirical and based on eyetracking measurements. Here we take first steps towards formalizing these processes for semantic ambiguities where we identified the presence of two features: (1) joint plausibility degrees of different possible interpretations, (2) causal structures according to which certain words play a more substantial role in the processes. The novel sheaf-theoretic model of definite causality developed by Gogioso and Pinzani in QPL 2021 offers tools to model and reason about these features. We applied this theory to a dataset of ambiguous phrases extracted from Psycholinguistics literature and their human plausibility judgements collected by us using the Amazon Mechanical Turk engine. We measured the causal fractions of different disambiguation orders within the phrases and discovered two prominent orders: from subject to verb in the subject-verb and from object to verb in the verb object phrases. We also found evidence for delay in the disambiguation of polysemous vs homonymous verbs, again compatible with Psycholinguistic findings.

Permutation invariant matrix statistics and computational language tasks

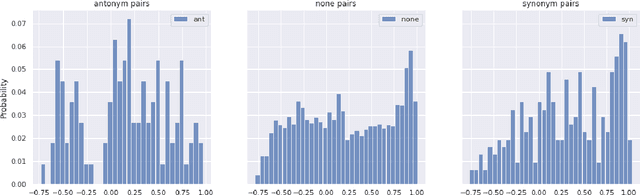
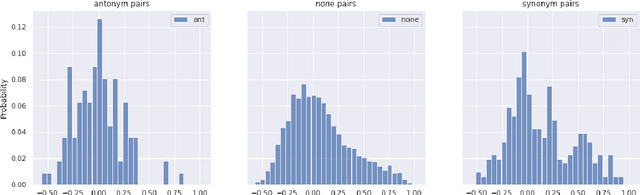
The Linguistic Matrix Theory programme introduced by Kartsaklis, Ramgoolam and Sadrzadeh is an approach to the statistics of matrices that are generated in type-driven distributional semantics, based on permutation invariant polynomial functions which are regarded as the key observables encoding the significant statistics. In this paper we generalize the previous results on the approximate Gaussianity of matrix distributions arising from compositional distributional semantics. We also introduce a geometry of observable vectors for words, defined by exploiting the graph-theoretic basis for the permutation invariants and the statistical characteristics of the ensemble of matrices associated with the words. We describe successful applications of this unified framework to a number of tasks in computational linguistics, associated with the distinctions between synonyms, antonyms, hypernyms and hyponyms.

Vector Space Semantics for Lambek Calculus with Soft Subexponentials

We develop a vector space semantics for Lambek Calculus with Soft Subexponentials, apply the calculus to construct compositional vector interpretations for parasitic gap noun phrases and discourse units with anaphora and ellipsis, and experiment with the constructions in a distributional sentence similarity task. As opposed to previous work, which used Lambek Calculus with a Relevant Modality the calculus used in this paper uses a bounded version of the modality and is decidable. The vector space semantics of this new modality allows us to meaningfully define contraction as projection and provide a linear theory behind what we could previously only achieve via nonlinear maps.