An Empirical Study of Conformal Prediction in LLM with ASP Scaffolds for Robust Reasoning

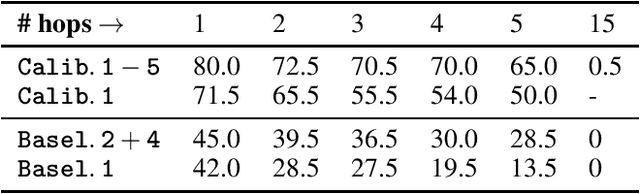
In this paper, we examine the use of Conformal Language Modelling (CLM) alongside Answer Set Programming (ASP) to enhance the performance of standard open-weight LLMs on complex multi-step reasoning tasks. Using the StepGame dataset, which requires spatial reasoning, we apply CLM to generate sets of ASP programs from an LLM, providing statistical guarantees on the correctness of the outputs. Experimental results show that CLM significantly outperforms baseline models that use standard sampling methods, achieving substantial accuracy improvements across different levels of reasoning complexity. Additionally, the LLM-as-Judge metric enhances CLM's performance, especially in assessing structurally and logically correct ASP outputs. However, calibrating CLM with diverse calibration sets did not improve generalizability for tasks requiring much longer reasoning steps, indicating limitations in handling more complex tasks.

DisCoCat for Donkey Sentences

We demonstrate how to parse Geach's Donkey sentences in a compositional distributional model of meaning. We build on previous work on the DisCoCat (Distributional Compositional Categorical) framework, including extensions that model discourse, determiners, and relative pronouns. We present a type-logical syntax for parsing donkey sentences, for which we define both relational and vector space semantics.

A Quantum Natural Language Processing Approach to Pronoun Resolution

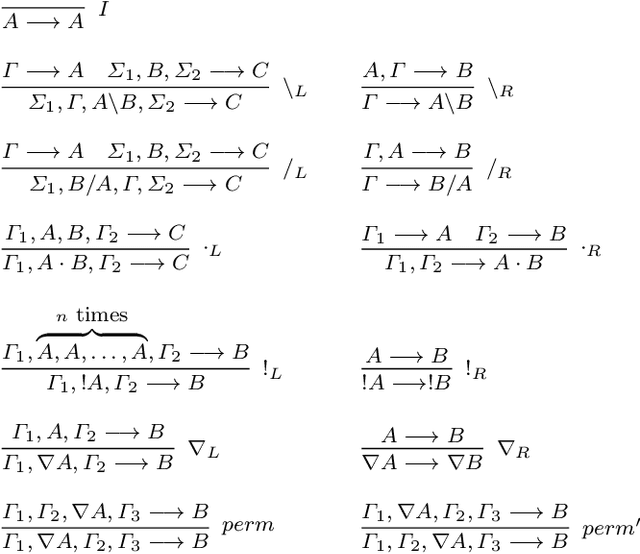
We use the Lambek Calculus with soft sub-exponential modalities to model and reason about discourse relations such as anaphora and ellipsis. A semantics for this logic is obtained by using truncated Fock spaces, developed in our previous work. We depict these semantic computations via a new string diagram. The Fock Space semantics has the advantage that its terms are learnable from large corpora of data using machine learning and they can be experimented with on mainstream natural language tasks. Further, and thanks to an existing translation from vector spaces to quantum circuits, we can also learn these terms on quantum computers and their simulators, such as the IBMQ range. We extend the existing translation to Fock spaces and develop quantum circuit semantics for discourse relations. We then experiment with the IBMQ AerSimulations of these circuits in a definite pronoun resolution task, where the highest accuracies were recorded for models when the anaphora was resolved.

Vector Space Semantics for Lambek Calculus with Soft Subexponentials

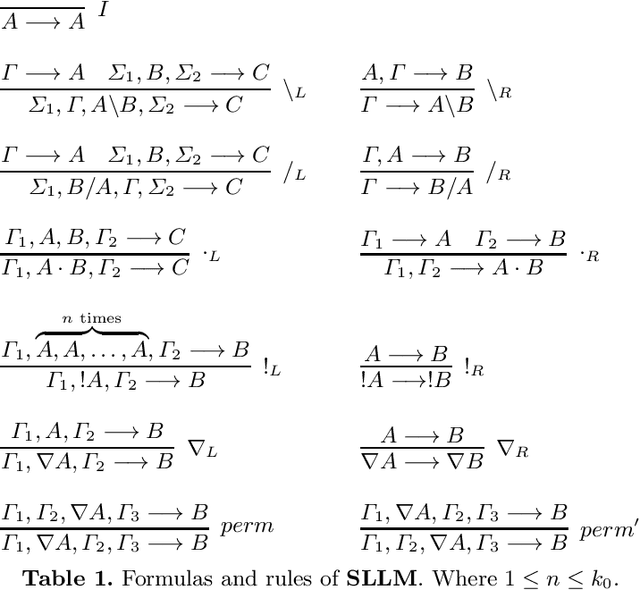
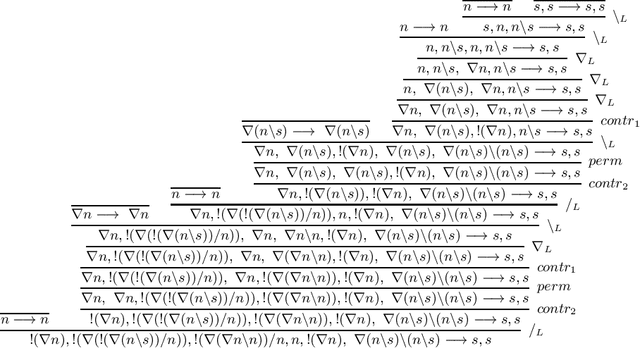
We develop a vector space semantics for Lambek Calculus with Soft Subexponentials, apply the calculus to construct compositional vector interpretations for parasitic gap noun phrases and discourse units with anaphora and ellipsis, and experiment with the constructions in a distributional sentence similarity task. As opposed to previous work, which used Lambek Calculus with a Relevant Modality the calculus used in this paper uses a bounded version of the modality and is decidable. The vector space semantics of this new modality allows us to meaningfully define contraction as projection and provide a linear theory behind what we could previously only achieve via nonlinear maps.

Categorical Vector Space Semantics for Lambek Calculus with a Relevant Modality

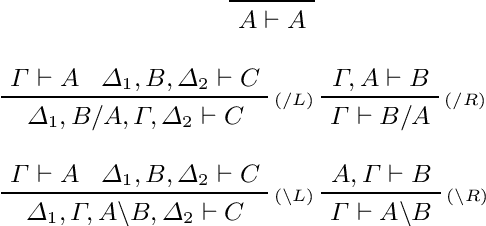
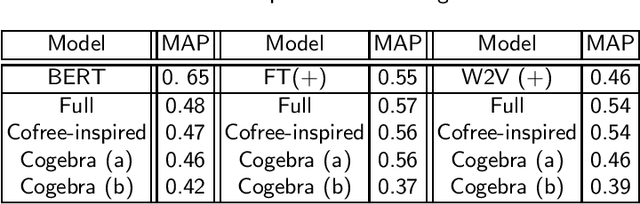
We develop a categorical compositional distributional semantics for Lambek Calculus with a Relevant Modality !L*, which has a limited edition of the contraction and permutation rules. The categorical part of the semantics is a monoidal biclosed category with a coalgebra modality, very similar to the structure of a Differential Category. We instantiate this category to finite dimensional vector spaces and linear maps via "quantisation" functors and work with three concrete interpretations of the coalgebra modality. We apply the model to construct categorical and concrete semantic interpretations for the motivating example of !L*: the derivation of a phrase with a parasitic gap. The effectiveness of the concrete interpretations are evaluated via a disambiguation task, on an extension of a sentence disambiguation dataset to parasitic gap phrases, using BERT, Word2Vec, and FastText vectors and Relational tensors.