Towards Transparency in Coreference Resolution: A Quantum-Inspired Approach

Guided by grammatical structure, words compose to form sentences, and guided by discourse structure, sentences compose to form dialogues and documents. The compositional aspect of sentence and discourse units is often overlooked by machine learning algorithms. A recent initiative called Quantum Natural Language Processing (QNLP) learns word meanings as points in a Hilbert space and acts on them via a translation of grammatical structure into Parametrised Quantum Circuits (PQCs). Previous work extended the QNLP translation to discourse structure using points in a closure of Hilbert spaces. In this paper, we evaluate this translation on a Winograd-style pronoun resolution task. We train a Variational Quantum Classifier (VQC) for binary classification and implement an end-to-end pronoun resolution system. The simulations executed on IBMQ software converged with an F1 score of 87.20%. The model outperformed two out of three classical coreference resolution systems and neared state-of-the-art SpanBERT. A mixed quantum-classical model yet improved these results with an F1 score increase of around 6%.

A Quantum Natural Language Processing Approach to Pronoun Resolution

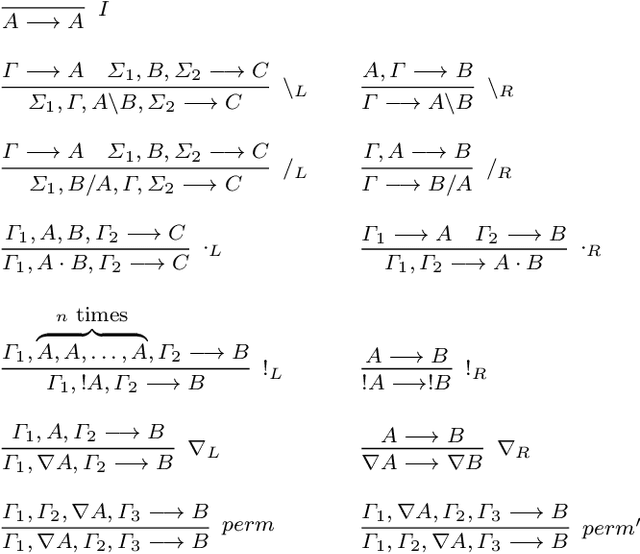
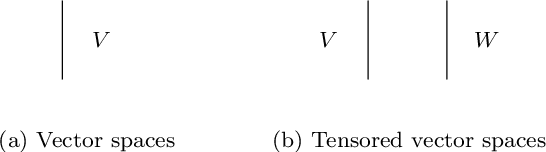
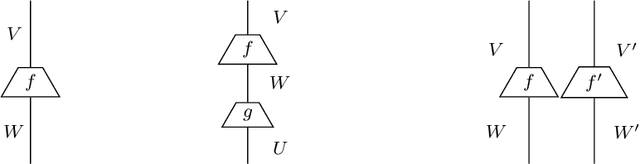
We use the Lambek Calculus with soft sub-exponential modalities to model and reason about discourse relations such as anaphora and ellipsis. A semantics for this logic is obtained by using truncated Fock spaces, developed in our previous work. We depict these semantic computations via a new string diagram. The Fock Space semantics has the advantage that its terms are learnable from large corpora of data using machine learning and they can be experimented with on mainstream natural language tasks. Further, and thanks to an existing translation from vector spaces to quantum circuits, we can also learn these terms on quantum computers and their simulators, such as the IBMQ range. We extend the existing translation to Fock spaces and develop quantum circuit semantics for discourse relations. We then experiment with the IBMQ AerSimulations of these circuits in a definite pronoun resolution task, where the highest accuracies were recorded for models when the anaphora was resolved.

Vector Space Semantics for Lambek Calculus with Soft Subexponentials

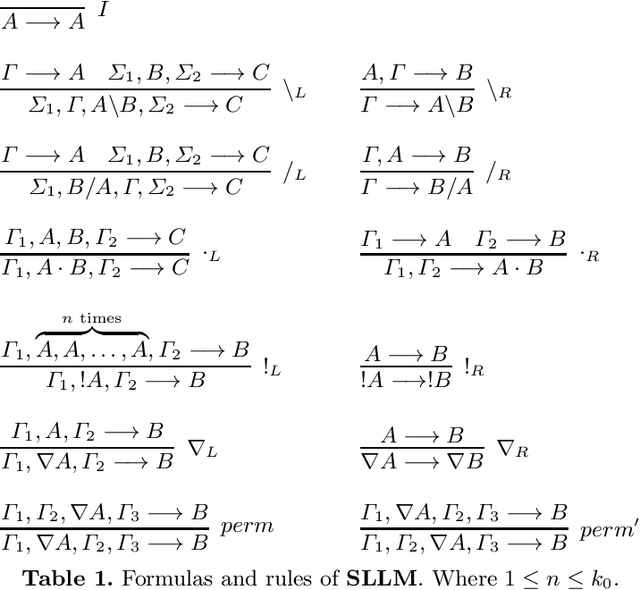
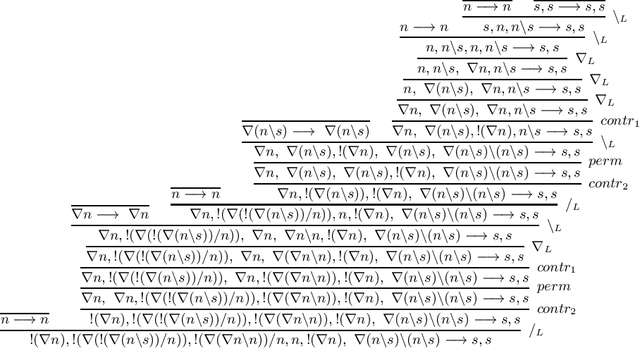
We develop a vector space semantics for Lambek Calculus with Soft Subexponentials, apply the calculus to construct compositional vector interpretations for parasitic gap noun phrases and discourse units with anaphora and ellipsis, and experiment with the constructions in a distributional sentence similarity task. As opposed to previous work, which used Lambek Calculus with a Relevant Modality the calculus used in this paper uses a bounded version of the modality and is decidable. The vector space semantics of this new modality allows us to meaningfully define contraction as projection and provide a linear theory behind what we could previously only achieve via nonlinear maps.

Categorical Vector Space Semantics for Lambek Calculus with a Relevant Modality

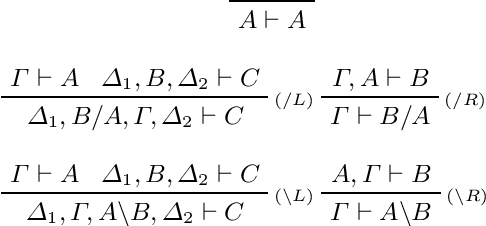
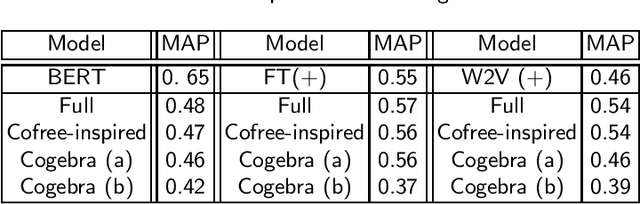
We develop a categorical compositional distributional semantics for Lambek Calculus with a Relevant Modality !L*, which has a limited edition of the contraction and permutation rules. The categorical part of the semantics is a monoidal biclosed category with a coalgebra modality, very similar to the structure of a Differential Category. We instantiate this category to finite dimensional vector spaces and linear maps via "quantisation" functors and work with three concrete interpretations of the coalgebra modality. We apply the model to construct categorical and concrete semantic interpretations for the motivating example of !L*: the derivation of a phrase with a parasitic gap. The effectiveness of the concrete interpretations are evaluated via a disambiguation task, on an extension of a sentence disambiguation dataset to parasitic gap phrases, using BERT, Word2Vec, and FastText vectors and Relational tensors.