Permutation invariant matrix statistics and computational language tasks

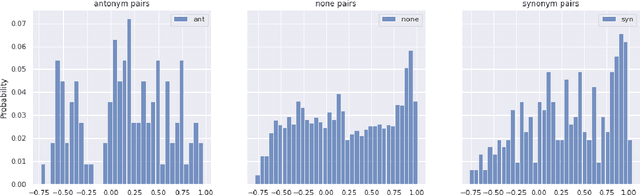
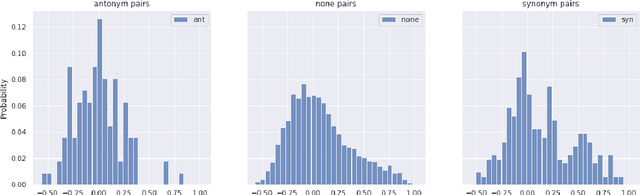
The Linguistic Matrix Theory programme introduced by Kartsaklis, Ramgoolam and Sadrzadeh is an approach to the statistics of matrices that are generated in type-driven distributional semantics, based on permutation invariant polynomial functions which are regarded as the key observables encoding the significant statistics. In this paper we generalize the previous results on the approximate Gaussianity of matrix distributions arising from compositional distributional semantics. We also introduce a geometry of observable vectors for words, defined by exploiting the graph-theoretic basis for the permutation invariants and the statistical characteristics of the ensemble of matrices associated with the words. We describe successful applications of this unified framework to a number of tasks in computational linguistics, associated with the distinctions between synonyms, antonyms, hypernyms and hyponyms.

Gaussianity and typicality in matrix distributional semantics

Constructions in type-driven compositional distributional semantics associate large collections of matrices of size $D$ to linguistic corpora. We develop the proposal of analysing the statistical characteristics of this data in the framework of permutation invariant matrix models. The observables in this framework are permutation invariant polynomial functions of the matrix entries, which correspond to directed graphs. Using the general 13-parameter permutation invariant Gaussian matrix models recently solved, we find, using a dataset of matrices constructed via standard techniques in distributional semantics, that the expectation values of a large class of cubic and quartic observables show high gaussianity at levels between 90 to 99 percent. Beyond expectation values, which are averages over words, the dataset allows the computation of standard deviations for each observable, which can be viewed as a measure of typicality for each observable. There is a wide range of magnitudes in the measures of typicality. The permutation invariant matrix models, considered as functions of random couplings, give a very good prediction of the magnitude of the typicality for different observables. We find evidence that observables with similar matrix model characteristics of Gaussianity and typicality also have high degrees of correlation between the ranked lists of words associated to these observables.

Permutation Invariant Gaussian Matrix Models

Permutation invariant Gaussian matrix models were recently developed for applications in computational linguistics. A 5-parameter family of models was solved. In this paper, we use a representation theoretic approach to solve the general 13-parameter Gaussian model, which can be viewed as a zero-dimensional quantum field theory. We express the two linear and eleven quadratic terms in the action in terms of representation theoretic parameters. These parameters are coefficients of simple quadratic expressions in terms of appropriate linear combinations of the matrix variables transforming in specific irreducible representations of the symmetric group $S_D$ where $D$ is the size of the matrices. They allow the identification of constraints which ensure a convergent Gaussian measure and well-defined expectation values for polynomial functions of the random matrix at all orders. A graph-theoretic interpretation is known to allow the enumeration of permutation invariants of matrices at linear, quadratic and higher orders. We express the expectation values of all the quadratic graph-basis invariants and a selection of cubic and quartic invariants in terms of the representation theoretic parameters of the model.

Linguistic Matrix Theory

Recent research in computational linguistics has developed algorithms which associate matrices with adjectives and verbs, based on the distribution of words in a corpus of text. These matrices are linear operators on a vector space of context words. They are used to construct the meaning of composite expressions from that of the elementary constituents, forming part of a compositional distributional approach to semantics. We propose a Matrix Theory approach to this data, based on permutation symmetry along with Gaussian weights and their perturbations. A simple Gaussian model is tested against word matrices created from a large corpus of text. We characterize the cubic and quartic departures from the model, which we propose, alongside the Gaussian parameters, as signatures for comparison of linguistic corpora. We propose that perturbed Gaussian models with permutation symmetry provide a promising framework for characterizing the nature of universality in the statistical properties of word matrices. The matrix theory framework developed here exploits the view of statistics as zero dimensional perturbative quantum field theory. It perceives language as a physical system realizing a universality class of matrix statistics characterized by permutation symmetry.