Manuel Accettulli Huber
Permutation invariant matrix statistics and computational language tasks
Feb 14, 2022
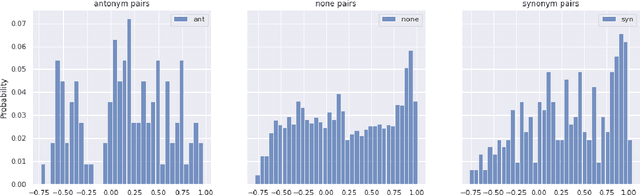

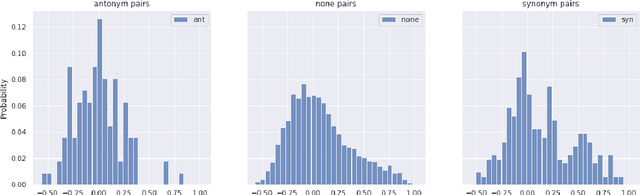
Abstract:The Linguistic Matrix Theory programme introduced by Kartsaklis, Ramgoolam and Sadrzadeh is an approach to the statistics of matrices that are generated in type-driven distributional semantics, based on permutation invariant polynomial functions which are regarded as the key observables encoding the significant statistics. In this paper we generalize the previous results on the approximate Gaussianity of matrix distributions arising from compositional distributional semantics. We also introduce a geometry of observable vectors for words, defined by exploiting the graph-theoretic basis for the permutation invariants and the statistical characteristics of the ensemble of matrices associated with the words. We describe successful applications of this unified framework to a number of tasks in computational linguistics, associated with the distinctions between synonyms, antonyms, hypernyms and hyponyms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge