Fundamental Components of Deep Learning: A category-theoretic approach

Deep learning, despite its remarkable achievements, is still a young field. Like the early stages of many scientific disciplines, it is marked by the discovery of new phenomena, ad-hoc design decisions, and the lack of a uniform and compositional mathematical foundation. From the intricacies of the implementation of backpropagation, through a growing zoo of neural network architectures, to the new and poorly understood phenomena such as double descent, scaling laws or in-context learning, there are few unifying principles in deep learning. This thesis develops a novel mathematical foundation for deep learning based on the language of category theory. We develop a new framework that is a) end-to-end, b) unform, and c) not merely descriptive, but prescriptive, meaning it is amenable to direct implementation in programming languages with sufficient features. We also systematise many existing approaches, placing many existing constructions and concepts from the literature under the same umbrella. In Part I we identify and model two main properties of deep learning systems parametricity and bidirectionality by we expand on the previously defined construction of actegories and Para to study the former, and define weighted optics to study the latter. Combining them yields parametric weighted optics, a categorical model of artificial neural networks, and more. Part II justifies the abstractions from Part I, applying them to model backpropagation, architectures, and supervised learning. We provide a lens-theoretic axiomatisation of differentiation, covering not just smooth spaces, but discrete settings of boolean circuits as well. We survey existing, and develop new categorical models of neural network architectures. We formalise the notion of optimisers and lastly, combine all the existing concepts together, providing a uniform and compositional framework for supervised learning.

Categorical Deep Learning: An Algebraic Theory of Architectures

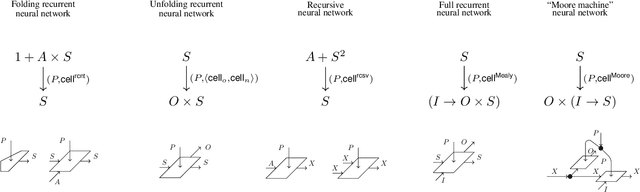
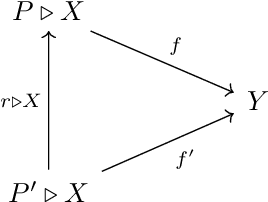
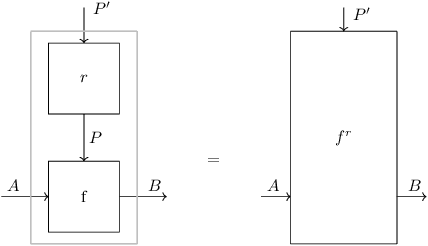
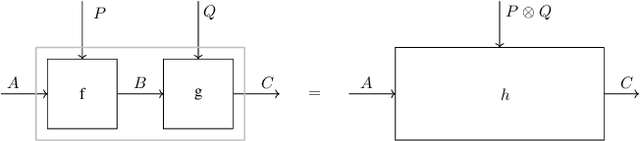
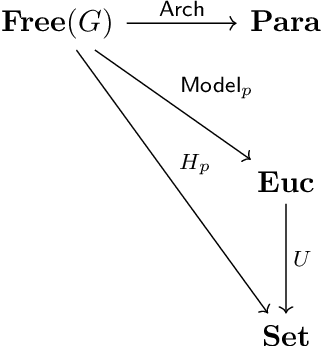
We present our position on the elusive quest for a general-purpose framework for specifying and studying deep learning architectures. Our opinion is that the key attempts made so far lack a coherent bridge between specifying constraints which models must satisfy and specifying their implementations. Focusing on building a such a bridge, we propose to apply category theory -- precisely, the universal algebra of monads valued in a 2-category of parametric maps -- as a single theory elegantly subsuming both of these flavours of neural network design. To defend our position, we show how this theory recovers constraints induced by geometric deep learning, as well as implementations of many architectures drawn from the diverse landscape of neural networks, such as RNNs. We also illustrate how the theory naturally encodes many standard constructs in computer science and automata theory.

Graph Convolutional Neural Networks as Parametric CoKleisli morphisms

We define the bicategory of Graph Convolutional Neural Networks $\mathbf{GCNN}_n$ for an arbitrary graph with $n$ nodes. We show it can be factored through the already existing categorical constructions for deep learning called $\mathbf{Para}$ and $\mathbf{Lens}$ with the base category set to the CoKleisli category of the product comonad. We prove that there exists an injective-on-objects, faithful 2-functor $\mathbf{GCNN}_n \to \mathbf{Para}(\mathsf{CoKl}(\mathbb{R}^{n \times n} \times -))$. We show that this construction allows us to treat the adjacency matrix of a GCNN as a global parameter instead of a a local, layer-wise one. This gives us a high-level categorical characterisation of a particular kind of inductive bias GCNNs possess. Lastly, we hypothesize about possible generalisations of GCNNs to general message-passing graph neural networks, connections to equivariant learning, and the (lack of) functoriality of activation functions.

Space-time tradeoffs of lenses and optics via higher category theory

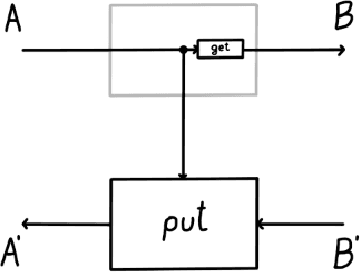
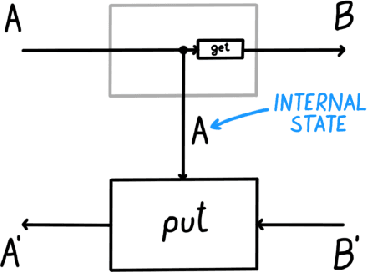
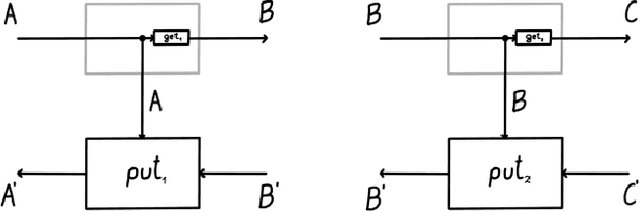
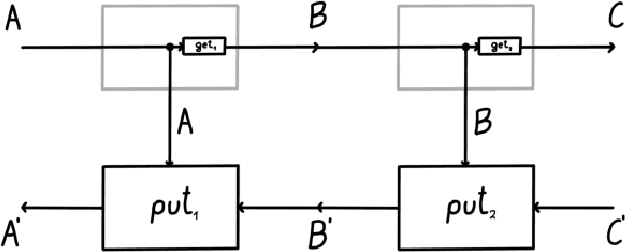
Optics and lenses are abstract categorical gadgets that model systems with bidirectional data flow. In this paper we observe that the denotational definition of optics - identifying two optics as equivalent by observing their behaviour from the outside - is not suitable for operational, software oriented approaches where optics are not merely observed, but built with their internal setups in mind. We identify operational differences between denotationally isomorphic categories of cartesian optics and lenses: their different composition rule and corresponding space-time tradeoffs, positioning them at two opposite ends of a spectrum. With these motivations we lift the existing categorical constructions and their relationships to the 2-categorical level, showing that the relevant operational concerns become visible. We define the 2-category $\textbf{2-Optic}(\mathcal{C})$ whose 2-cells explicitly track optics' internal configuration. We show that the 1-category $\textbf{Optic}(\mathcal{C})$ arises by locally quotienting out the connected components of this 2-category. We show that the embedding of lenses into cartesian optics gets weakened from a functor to an oplax functor whose oplaxator now detects the different composition rule. We determine the difficulties in showing this functor forms a part of an adjunction in any of the standard 2-categories. We establish a conjecture that the well-known isomorphism between cartesian lenses and optics arises out of the lax 2-adjunction between their double-categorical counterparts. In addition to presenting new research, this paper is also meant to be an accessible introduction to the topic.

Category Theory in Machine Learning

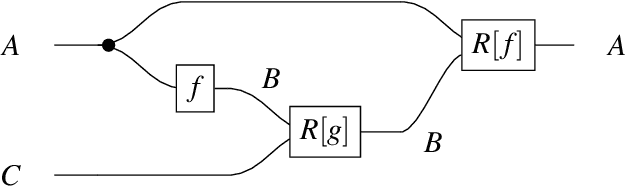
Over the past two decades machine learning has permeated almost every realm of technology. At the same time, many researchers have begun using category theory as a unifying language, facilitating communication between different scientific disciplines. It is therefore unsurprising that there is a burgeoning interest in applying category theory to machine learning. We aim to document the motivations, goals and common themes across these applications. We touch on gradient-based learning, probability, and equivariant learning.

Categorical Foundations of Gradient-Based Learning

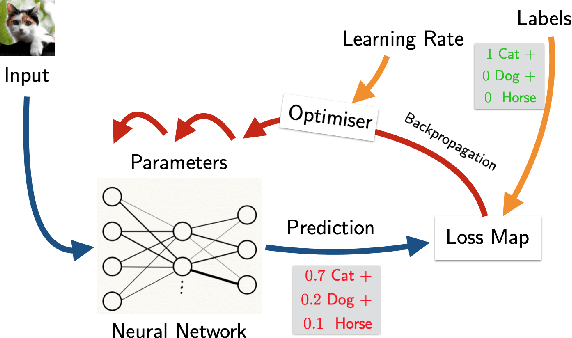
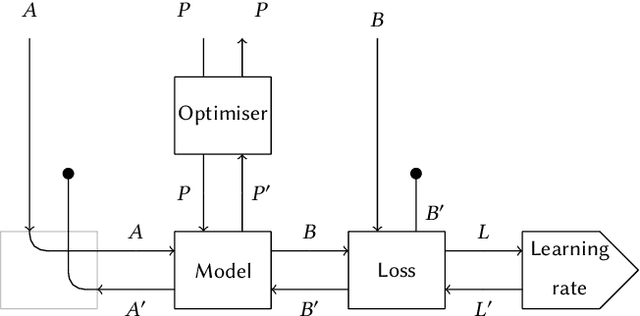
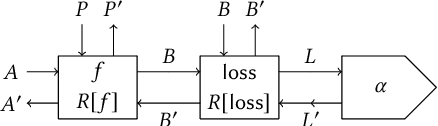
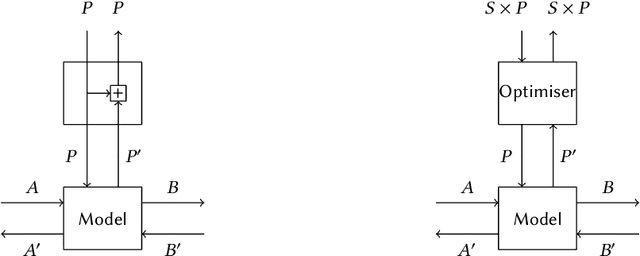
We propose a categorical foundation of gradient-based machine learning algorithms in terms of lenses, parametrised maps, and reverse derivative categories. This foundation provides a powerful explanatory and unifying framework: it encompasses a variety of gradient descent algorithms such as ADAM, AdaGrad, and Nesterov momentum, as well as a variety of loss functions such as as MSE and Softmax cross-entropy, shedding new light on their similarities and differences. Our approach also generalises beyond neural networks (modelled in categories of smooth maps), accounting for other structures relevant to gradient-based learning such as boolean circuits. Finally, we also develop a novel implementation of gradient-based learning in Python, informed by the principles introduced by our framework.

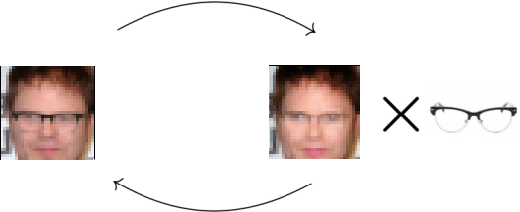
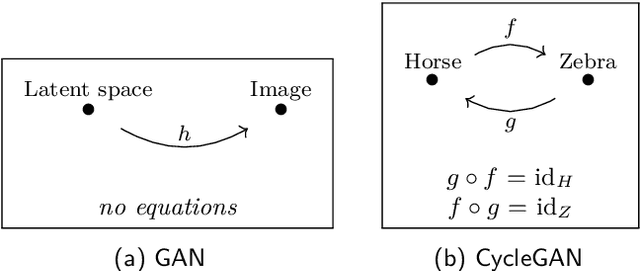
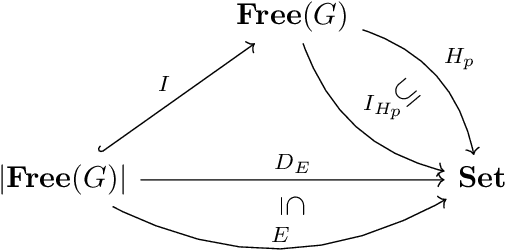
Learning Functors using Gradient Descent

Neural networks are a general framework for differentiable optimization which includes many other machine learning approaches as special cases. In this paper we build a category-theoretic formalism around a neural network system called CycleGAN. CycleGAN is a general approach to unpaired image-to-image translation that has been getting attention in the recent years. Inspired by categorical database systems, we show that CycleGAN is a "schema", i.e. a specific category presented by generators and relations, whose specific parameter instantiations are just set-valued functors on this schema. We show that enforcing cycle-consistencies amounts to enforcing composition invariants in this category. We generalize the learning procedure to arbitrary such categories and show a special class of functors, rather than functions, can be learned using gradient descent. Using this framework we design a novel neural network system capable of learning to insert and delete objects from images without paired data. We qualitatively evaluate the system on the CelebA dataset and obtain promising results.

Compositional Deep Learning

Neural networks have become an increasingly popular tool for solving many real-world problems. They are a general framework for differentiable optimization which includes many other machine learning approaches as special cases. In this thesis we build a category-theoretic formalism around a class of neural networks exemplified by CycleGAN. CycleGAN is a collection of neural networks, closed under composition, whose inductive bias is increased by enforcing composition invariants, i.e. cycle-consistencies. Inspired by Functorial Data Migration, we specify the interconnection of these networks using a categorical schema, and network instances as set-valued functors on this schema. We also frame neural network architectures, datasets, models, and a number of other concepts in a categorical setting and thus show a special class of functors, rather than functions, can be learned using gradient descent. We use the category-theoretic framework to conceive a novel neural network architecture whose goal is to learn the task of object insertion and object deletion in images with unpaired data. We test the architecture on three different datasets and obtain promising results.