Learning Functors using Gradient Descent
Paper and Code
Sep 15, 2020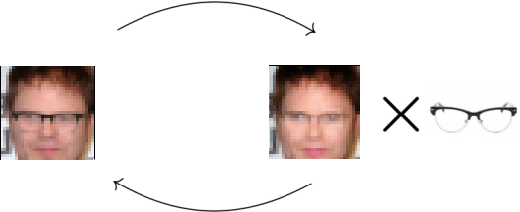
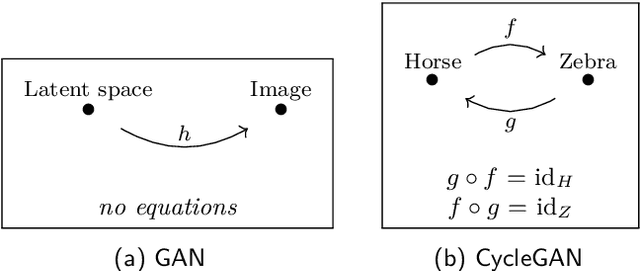
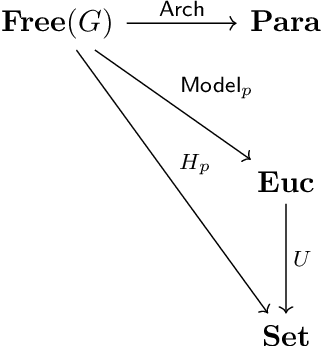
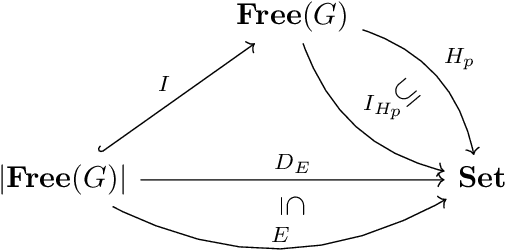
Neural networks are a general framework for differentiable optimization which includes many other machine learning approaches as special cases. In this paper we build a category-theoretic formalism around a neural network system called CycleGAN. CycleGAN is a general approach to unpaired image-to-image translation that has been getting attention in the recent years. Inspired by categorical database systems, we show that CycleGAN is a "schema", i.e. a specific category presented by generators and relations, whose specific parameter instantiations are just set-valued functors on this schema. We show that enforcing cycle-consistencies amounts to enforcing composition invariants in this category. We generalize the learning procedure to arbitrary such categories and show a special class of functors, rather than functions, can be learned using gradient descent. Using this framework we design a novel neural network system capable of learning to insert and delete objects from images without paired data. We qualitatively evaluate the system on the CelebA dataset and obtain promising results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge