Graph Convolutional Neural Networks as Parametric CoKleisli morphisms

We define the bicategory of Graph Convolutional Neural Networks $\mathbf{GCNN}_n$ for an arbitrary graph with $n$ nodes. We show it can be factored through the already existing categorical constructions for deep learning called $\mathbf{Para}$ and $\mathbf{Lens}$ with the base category set to the CoKleisli category of the product comonad. We prove that there exists an injective-on-objects, faithful 2-functor $\mathbf{GCNN}_n \to \mathbf{Para}(\mathsf{CoKl}(\mathbb{R}^{n \times n} \times -))$. We show that this construction allows us to treat the adjacency matrix of a GCNN as a global parameter instead of a a local, layer-wise one. This gives us a high-level categorical characterisation of a particular kind of inductive bias GCNNs possess. Lastly, we hypothesize about possible generalisations of GCNNs to general message-passing graph neural networks, connections to equivariant learning, and the (lack of) functoriality of activation functions.

Feature Importance for Time Series Data: Improving KernelSHAP

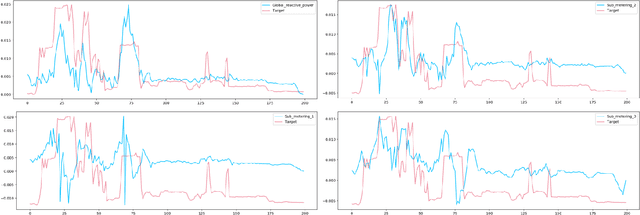
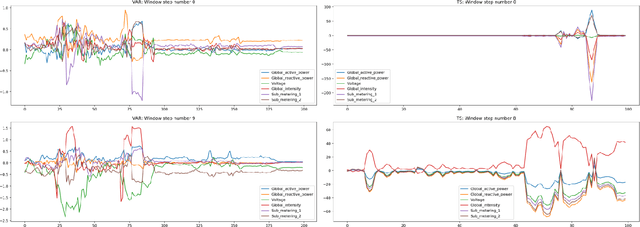
Feature importance techniques have enjoyed widespread attention in the explainable AI literature as a means of determining how trained machine learning models make their predictions. We consider Shapley value based approaches to feature importance, applied in the context of time series data. We present closed form solutions for the SHAP values of a number of time series models, including VARMAX. We also show how KernelSHAP can be applied to time series tasks, and how the feature importances that come from this technique can be combined to perform "event detection". Finally, we explore the use of Time Consistent Shapley values for feature importance.