Functorial Manifold Learning and Overlapping Clustering
Paper and Code
Nov 15, 2020
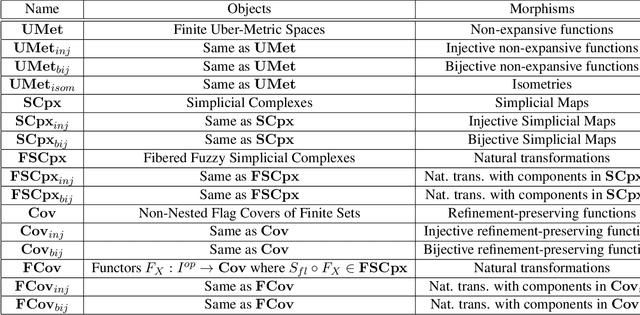
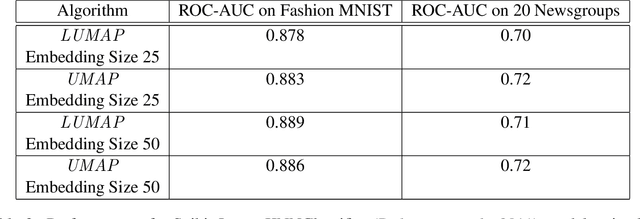
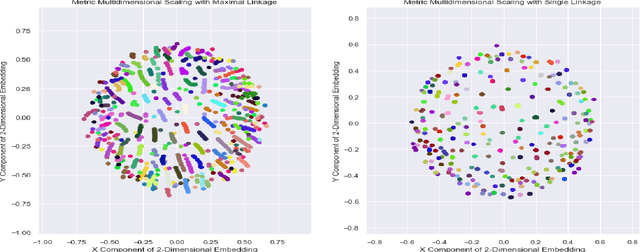
We adapt previous research on topological unsupervised learning to develop a unified functorial perspective on manifold learning and clustering. We first introduce overlapping hierachical clustering algorithms as functors and demonstrate that the maximal and single linkage clustering algorithms factor through an adaptation of the singular set functor. Next, we characterize manifold learning algorithms as functors that map uber-metric spaces to optimization objectives and factor through hierachical clustering functors. We use this characterization to prove refinement bounds on manifold learning loss functions and construct a hierarchy of manifold learning algorithms based on their invariants. We express several state of the art manifold learning algorithms as functors at different levels of this hierarchy, including Laplacian Eigenmaps, Metric Multidimensional Scaling, and UMAP. Finally, we experimentally demonstrate that this perspective enables us to derive and analyze novel manifold learning algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge